8. 若$y= (a+4)x^{|a|-2}+5x-8是关于x$的二次函数,则$a$的值为 ( )
A.$-4$
B.$4$
C.$\pm4$
D.$\pm2$
A.$-4$
B.$4$
C.$\pm4$
D.$\pm2$
答案:
B
9. 如图,在四边形$ABCD$中,$\angle BAD= \angle ACB= 90^{\circ}$,$AB= AD$,$AC= 4BC$.设$CD的长为x$,四边形$ABCD的面积为y$,则$y与x$之间的函数解析式为 ( )

A.$y= \frac{2}{25}x^{2}$
B.$y= \frac{4}{25}x^{2}$
C.$y= \frac{2}{5}x^{2}$
D.$y= \frac{4}{5}x^{2}$

A.$y= \frac{2}{25}x^{2}$
B.$y= \frac{4}{25}x^{2}$
C.$y= \frac{2}{5}x^{2}$
D.$y= \frac{4}{5}x^{2}$
答案:
C 解析:如图,过点 D 作 DE⊥AC 于点 E.设 BC=a,则 AC=4a.
∵∠BAD=90°,∠DEA=90°,
∴易得∠BAC=∠ADE.又
∵∠ACB=∠DEA=90°,AB=DA,
∴△ABC≌△DAE.
∴BC=AE=a,AC=DE=4a.
∴CE=AC - AE=4a - a=3a.在 Rt△DEC 中,$ CD=\sqrt{CE^{2}+DE^{2}}=\sqrt{(3a)^{2}+(4a)^{2}}=5a $,
∴x=5a,即$ a=\frac{1}{5}x $.
∴$ y=S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}BC\cdot AC+\frac{1}{2}AC\cdot DE=\frac{1}{2}\cdot a\cdot4a+\frac{1}{2}\cdot4a\cdot4a=10a^{2}=\frac{2}{5}x^{2} $,即 y 与 x 之间的函数解析式为$ y=\frac{2}{5}x^{2} $.
C 解析:如图,过点 D 作 DE⊥AC 于点 E.设 BC=a,则 AC=4a.
∵∠BAD=90°,∠DEA=90°,
∴易得∠BAC=∠ADE.又
∵∠ACB=∠DEA=90°,AB=DA,
∴△ABC≌△DAE.
∴BC=AE=a,AC=DE=4a.
∴CE=AC - AE=4a - a=3a.在 Rt△DEC 中,$ CD=\sqrt{CE^{2}+DE^{2}}=\sqrt{(3a)^{2}+(4a)^{2}}=5a $,
∴x=5a,即$ a=\frac{1}{5}x $.
∴$ y=S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}BC\cdot AC+\frac{1}{2}AC\cdot DE=\frac{1}{2}\cdot a\cdot4a+\frac{1}{2}\cdot4a\cdot4a=10a^{2}=\frac{2}{5}x^{2} $,即 y 与 x 之间的函数解析式为$ y=\frac{2}{5}x^{2} $.

10. 已知$y= (k-2)x^{|k|}+2x-3是关于x$的二次函数,则实数$k$的值为______.
答案:
-2
11. 已知函数$y= (m^{2}-m)x^{2}+(m-1)x-2$($m$为常数).
(1)若这个函数是关于$x$的一次函数,求$m$的值;
(2)若这个函数是关于$x$的二次函数,求$m$的取值范围.
(1)若这个函数是关于$x$的一次函数,求$m$的值;
(2)若这个函数是关于$x$的二次函数,求$m$的取值范围.
答案:
11.
(1)由题意,得$ \begin{cases} m^{2}-m=0, \\ m-1\neq0, \end{cases} $解得 m=0
(2)由题意,得$ m^{2}-m\neq0 $,解得 m≠0 且 m≠1
(1)由题意,得$ \begin{cases} m^{2}-m=0, \\ m-1\neq0, \end{cases} $解得 m=0
(2)由题意,得$ m^{2}-m\neq0 $,解得 m≠0 且 m≠1
12. 如图,利用一面长为34 m的墙,用铁栅栏围成一个矩形自行车停放场地$ABCD$,在边$AB和BC$上各有一个2 m宽的小门(不用铁栅栏).若所用铁栅栏的长为40 m,矩形$ABCD的边AD的长为x$ m,边$AB的长为y$ m,矩形的面积为$S$ $m^{2}$,且$x<y$.
(1)求$S与x$之间的函数解析式,并指出该函数的类型;
(2)请直接写出自变量$x$的取值范围.

(1)求$S与x$之间的函数解析式,并指出该函数的类型;
(2)请直接写出自变量$x$的取值范围.

答案:
12.
(1)由题意,得$ S=xy=x(40 + 2×2 - 2x)=-2x^{2}+44x $,这是一个二次函数
(2)自变量 x 的取值范围是$ 5\leqslant x<\frac{44}{3} $
(1)由题意,得$ S=xy=x(40 + 2×2 - 2x)=-2x^{2}+44x $,这是一个二次函数
(2)自变量 x 的取值范围是$ 5\leqslant x<\frac{44}{3} $
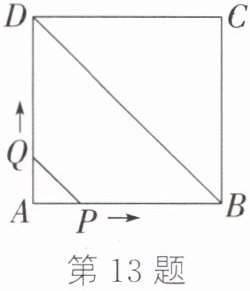
13. 如图,正方形$ABCD$的边长为4 cm,动点$P,Q同时从点A$出发,以1 cm/s的速度分别沿$A→B→C和A→D→C的路径向点C$运动.设运动时间为$x$ s,由点$P,B,D,Q确定的封闭图形的面积为y$ $cm^{2}$,求$y与x(0\leq x\leq8)$之间的函数解析式.

答案:
13. 由题意,可知当 0≤x≤4 时,AP=AQ=x cm,
∴$ y=\frac{1}{2}×4×4-\frac{1}{2}x^{2}=8-\frac{1}{2}x^{2} $.当 4<x≤8 时,$ CQ=CP=4 + 4 - x=(8 - x) $cm,
∴$ y=\frac{1}{2}×4×4-\frac{1}{2}(8 - x)^{2}=-\frac{1}{2}x^{2}+8x - 24 $.综上所述,y 与 x 之间的函数解析式为$ y=\begin{cases} 8-\frac{1}{2}x^{2}(0\leqslant x\leqslant4), \\ -\frac{1}{2}x^{2}+8x - 24(4<x\leqslant8) \end{cases} $
∴$ y=\frac{1}{2}×4×4-\frac{1}{2}x^{2}=8-\frac{1}{2}x^{2} $.当 4<x≤8 时,$ CQ=CP=4 + 4 - x=(8 - x) $cm,
∴$ y=\frac{1}{2}×4×4-\frac{1}{2}(8 - x)^{2}=-\frac{1}{2}x^{2}+8x - 24 $.综上所述,y 与 x 之间的函数解析式为$ y=\begin{cases} 8-\frac{1}{2}x^{2}(0\leqslant x\leqslant4), \\ -\frac{1}{2}x^{2}+8x - 24(4<x\leqslant8) \end{cases} $
查看更多完整答案,请扫码查看


