《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

7. 如图,在Rt△ABC中,∠C= 90°,AB= 10 cm,BC= 8 cm,点P从点A出发,沿AC向点C以1 cm/s的速度运动；同时点Q从点C出发,沿CB向点B以2 cm/s的速度运动(当点Q运动到点B时,点P,Q同时停止运动).在运动过程中,四边形PABQ面积的最小值为( )

A.$ 19\ cm^2 $
B.$ 16\ cm^2 $
C.$ 15\ cm^2 $
D.$ 12\ cm^2 $

答案： C

8. 如图所示为一块边长为6 cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的虚线折起,做成一个无盖的直三棱柱纸盒,则这个纸盒的侧面积最大为______.

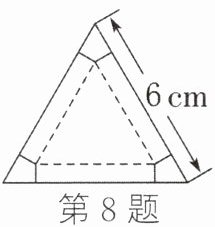
答案： $\frac{9\sqrt{3}}{2}\ cm^{2}$

9. 如图,将边长为40 cm的正方形硬纸板的四个角各剪掉一个同样大小的小正方形,剩余部分折成一个无盖的盒子(纸板的厚度忽略不计).
(1)若该无盖盒子的底面积为$900 cm^2,$求剪掉的小正方形的边长；
(2)折成的无盖盒子的侧面积最大为多少平方厘米？

答案： （1）设剪掉的小正方形的边长为x cm,则$(40-2x)^{2}=900$,即$40-2x=\pm30$,解得$x_{1}=35$(不合题意,舍去),$x_{2}=5$.$\therefore$ 剪掉的小正方形的边长为5 cm （2）设剪掉的小正方形的边长为a cm,盒子的侧面积为$y\ cm^{2}$,则y与a之间的函数解析式为$y=4(40-2a)a=-8(a-10)^{2}+800$.$\because -8＜0$,$\therefore$ 当$a=10$时,y取得最大值,为800.$\therefore$ 折成的无盖盒子的侧面积最大为$800\ cm^{2}$

10. (2023·菏泽)某学校为美化校园环境,打造绿色校园,决定用篱笆围成一个一面靠墙(墙足够长)的矩形花园(如图),用一道篱笆把花园分为A,B两块,花园里种满牡丹和芍药.学校已定购篱笆120米.
(1)设计一个使花园面积最大的方案,并求出其最大面积；
(2)在花园面积最大的条件下,A,B两块内分别种植牡丹和芍药,每平方米种植2株,已知牡丹每株的售价为25元,芍药每株的售价为15元,学校计划购买费用不超过5万元,则最多可以购买多少株牡丹？

答案： （1）设花园与墙平行的一边长为x米,面积为y平方米,则不与墙平行的边长为$\frac{120-x}{3}$米.$\therefore y=x\cdot \frac{120-x}{3}=-\frac{1}{3}x^{2}+40x=-\frac{1}{3}(x-60)^{2}+1200$.$\because -\frac{1}{3}＜0$,$\therefore$ 当$x=60$时,y取得最大值,为1200,此时不与墙平行的边长为$\frac{120-60}{3}=20$(米).$\therefore$ 使花园面积最大的方案为与墙平行的一边长为60米,不与墙平行的边长为20米,且最大面积为1200平方米 （2）设种植牡丹的面积为a平方米,则种植芍药的面积为$(1200-a)$平方米.由题意,得$25×2a+15×2(1200-a)\leq50000$,解得$a\leq700$.$\therefore$ 牡丹最多种植700平方米.$\therefore$ 最多可以购买$700×2=1400$(株)牡丹