1. 二次函数的解析式通常有以下几种形式:
(1)一般式:y= ______;
(2)顶点式:y= ______;
(3)交点式:y= ______
______.
2. 用待定系数法确定二次函数解析式的步骤如下:
第一步,设:______;
第二步,代:______;
第三步,解:______;
第四步,还原:______.
(1)一般式:y= ______;
(2)顶点式:y= ______;
(3)交点式:y= ______
______.
2. 用待定系数法确定二次函数解析式的步骤如下:
第一步,设:______;
第二步,代:______;
第三步,解:______;
第四步,还原:______.
答案:
1.(1)$ax^{2}+bx+c$(a,b,c为常数,$a≠0$)(2)$a(x - h)^{2}+k$(a,h,k为常数,$a≠0$)(3)$a(x - x_{1})(x - x_{2})$($x_{1},x_{2}$为函数图象与x轴交点的横坐标,$a≠0$)
2. 根据题目中所给的条件设出二次函数的解析式,代入点的坐标,得到方程(组),解方程(组),将求出的待定系数还原到解析式中
2. 根据题目中所给的条件设出二次函数的解析式,代入点的坐标,得到方程(组),解方程(组),将求出的待定系数还原到解析式中
1. (教材P40练习第2题变式)若抛物线经过(0,1),(-1,0),(1,0)三点,则此抛物线对应的函数解析式为( )
A.$y= x^2+1$
B.$y= x^2-1$
C.$y= -x^2+1$
D.$y= -x^2-1$
A.$y= x^2+1$
B.$y= x^2-1$
C.$y= -x^2+1$
D.$y= -x^2-1$
答案:
C
2. 已知抛物线$y= x^2+bx+c$经过点(3,1),(-1,1),则此抛物线还经过点( )
A.(1,2)
B.(0,-2)
C.(-5,2)
D.(-2,0)
A.(1,2)
B.(0,-2)
C.(-5,2)
D.(-2,0)
答案:
B
3. 若抛物线$y= ax^2+bx+5(a\neq0)$的顶点坐标是(-1,-4),则a= ______,b= ______.
答案:
9 18
4. (1)已知二次函数图象的对称轴为直线x= -2,顶点在x轴上,且与y轴交于点(0,3),则该二次函数的解析式为______;
(2)已知二次函数图象的顶点坐标为(-2,-5),且过点(1,-14),则该二次函数的解析式为______;
(3)已知二次函数在$x= \frac{3}{2}$时,有最小值$-\frac{1}{4}$,且函数图象经过点(0,2),则该二次函数的解析式为______.
(2)已知二次函数图象的顶点坐标为(-2,-5),且过点(1,-14),则该二次函数的解析式为______;
(3)已知二次函数在$x= \frac{3}{2}$时,有最小值$-\frac{1}{4}$,且函数图象经过点(0,2),则该二次函数的解析式为______.
答案:
4.(1)$y = \frac{3}{4}x^{2}+3x + 3$ 解析:由题意,可设$y = a(x + 2)^{2}$.将(0,3)代入,得$4a = 3$,解得$a = \frac{3}{4}$.
∴$y = \frac{3}{4}(x + 2)^{2}=\frac{3}{4}x^{2}+3x + 3$.
(2)$y = -x^{2}-4x - 9$ 解析:由题意,可设$y = a(x + 2)^{2}-5$.将(1,-14)代入,得$9a - 5 = -14$,解得$a = -1$.
∴$y = -(x + 2)^{2}-5=-x^{2}-4x - 9$.
(3)$y = x^{2}-3x + 2$ 解析:由题意,可设$y = a(x - \frac{3}{2})^{2}-\frac{1}{4}$.将(0,2)代入,得$\frac{9}{4}a - \frac{1}{4}=2$,解得$a = 1$.
∴$y=(x - \frac{3}{2})^{2}-\frac{1}{4}=x^{2}-3x + 2$.
∴$y = \frac{3}{4}(x + 2)^{2}=\frac{3}{4}x^{2}+3x + 3$.
(2)$y = -x^{2}-4x - 9$ 解析:由题意,可设$y = a(x + 2)^{2}-5$.将(1,-14)代入,得$9a - 5 = -14$,解得$a = -1$.
∴$y = -(x + 2)^{2}-5=-x^{2}-4x - 9$.
(3)$y = x^{2}-3x + 2$ 解析:由题意,可设$y = a(x - \frac{3}{2})^{2}-\frac{1}{4}$.将(0,2)代入,得$\frac{9}{4}a - \frac{1}{4}=2$,解得$a = 1$.
∴$y=(x - \frac{3}{2})^{2}-\frac{1}{4}=x^{2}-3x + 2$.
5. (2023·宁波)如图,二次函数$y= x^2+bx+c$的图象经过A(1,-2),B(0,-5)两点.
(1)求该二次函数的解析式及图象的顶点坐标;
(2)当$y\leq-2$时,请根据图象求x的取值范围.
]
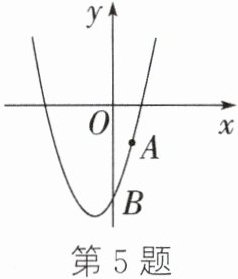
(1)求该二次函数的解析式及图象的顶点坐标;
(2)当$y\leq-2$时,请根据图象求x的取值范围.
]

答案:
(1)
∵二次函数$y = x^{2}+bx + c$的图象经过$A(1,-2)$,$B(0,-5)$两点,
∴$\begin{cases}1 + b + c = -2\\c = -5\end{cases}$,解得$\begin{cases}b = 2\\c = -5\end{cases}$,
∴该二次函数的解析式为$y = x^{2}+2x - 5=(x + 1)^{2}-6$.
∴该二次函数图象的顶点坐标为$(-1,-6)$
(2)当$y = -2$时,$(x + 1)^{2}-6 = -2$,
∴$(x + 1)^{2}=4$,解得$x_{1}=1$,$x_{2}=-3$.
∴由图象可知,当$y\leq -2$时,$-3\leq x\leq 1$
∵二次函数$y = x^{2}+bx + c$的图象经过$A(1,-2)$,$B(0,-5)$两点,
∴$\begin{cases}1 + b + c = -2\\c = -5\end{cases}$,解得$\begin{cases}b = 2\\c = -5\end{cases}$,
∴该二次函数的解析式为$y = x^{2}+2x - 5=(x + 1)^{2}-6$.
∴该二次函数图象的顶点坐标为$(-1,-6)$
(2)当$y = -2$时,$(x + 1)^{2}-6 = -2$,
∴$(x + 1)^{2}=4$,解得$x_{1}=1$,$x_{2}=-3$.
∴由图象可知,当$y\leq -2$时,$-3\leq x\leq 1$
6. (2023·鸡西)如图,抛物线$y= ax^2+bx+3$与x轴交于A(-3,0),B(1,0)两点,交y轴于点C.
(1)求抛物线对应的函数解析式.
(2)抛物线上是否存在一点P,使得$S_{\triangle PBC}= \frac{1}{2}S_{\triangle ABC}$?若存在,请求出点P的坐标;若不存在,请说明理由.
]

(1)求抛物线对应的函数解析式.
(2)抛物线上是否存在一点P,使得$S_{\triangle PBC}= \frac{1}{2}S_{\triangle ABC}$?若存在,请求出点P的坐标;若不存在,请说明理由.
]

答案:
6.(1)把$A(-3,0)$,$B(1,0)$代入$y = ax^{2}+bx + 3$,得$\begin{cases}9a - 3b + 3 = 0\\a + b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1\\b = -2\end{cases}$,
∴抛物线对应的函数解析式为$y = -x^{2}-2x + 3$
(2)存在
∵$A(-3,0)$,$B(1,0)$,
∴$AB = 4$.在$y = -x^{2}-2x + 3$中,令$x = 0$,则$y = 3$,
∴$C(0,3)$.
∴$OC = 3$.
∴$S_{\triangle ABC}=\frac{1}{2}AB\cdot OC=\frac{1}{2}×4×3 = 6$.
∴$S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=3$.
如图,过点P作$PE// x$轴交BC于点E,连接BP,CP.设直线BC对应的函数解析式为$y = mx + n$.将$B(1,0)$,$C(0,3)$代入,得$\begin{cases}m + n = 0\\n = 3\end{cases}$,解得$\begin{cases}m = -3\\n = 3\end{cases}$,
∴直线BC对应的函数解析式为$y = -3x + 3$.
设$P(t,-t^{2}-2t + 3)$,则易得$E(\frac{t^{2}+2t}{3},-t^{2}-2t + 3)$.
∴$PE=\frac{t^{2}+2t}{3}-t=\frac{t^{2}-t}{3}$.
∴$S_{\triangle PBC}=\frac{1}{2}×\frac{t^{2}-t}{3}×3 = 3$,解得$t = -2$或$t = 3$.
∴点P的纵坐标为$-(-2)^{2}-2×(-2)+3 = 3$或$-3^{2}-2×3 + 3 = -12$.
∴点P的坐标为$(-2,3)$或$(3,-12)$

6.(1)把$A(-3,0)$,$B(1,0)$代入$y = ax^{2}+bx + 3$,得$\begin{cases}9a - 3b + 3 = 0\\a + b + 3 = 0\end{cases}$,解得$\begin{cases}a = -1\\b = -2\end{cases}$,
∴抛物线对应的函数解析式为$y = -x^{2}-2x + 3$
(2)存在
∵$A(-3,0)$,$B(1,0)$,
∴$AB = 4$.在$y = -x^{2}-2x + 3$中,令$x = 0$,则$y = 3$,
∴$C(0,3)$.
∴$OC = 3$.
∴$S_{\triangle ABC}=\frac{1}{2}AB\cdot OC=\frac{1}{2}×4×3 = 6$.
∴$S_{\triangle PBC}=\frac{1}{2}S_{\triangle ABC}=3$.
如图,过点P作$PE// x$轴交BC于点E,连接BP,CP.设直线BC对应的函数解析式为$y = mx + n$.将$B(1,0)$,$C(0,3)$代入,得$\begin{cases}m + n = 0\\n = 3\end{cases}$,解得$\begin{cases}m = -3\\n = 3\end{cases}$,
∴直线BC对应的函数解析式为$y = -3x + 3$.
设$P(t,-t^{2}-2t + 3)$,则易得$E(\frac{t^{2}+2t}{3},-t^{2}-2t + 3)$.
∴$PE=\frac{t^{2}+2t}{3}-t=\frac{t^{2}-t}{3}$.
∴$S_{\triangle PBC}=\frac{1}{2}×\frac{t^{2}-t}{3}×3 = 3$,解得$t = -2$或$t = 3$.
∴点P的纵坐标为$-(-2)^{2}-2×(-2)+3 = 3$或$-3^{2}-2×3 + 3 = -12$.
∴点P的坐标为$(-2,3)$或$(3,-12)$

查看更多完整答案,请扫码查看


