《2025年通成学典课时作业本九年级数学上册人教版浙江专版》

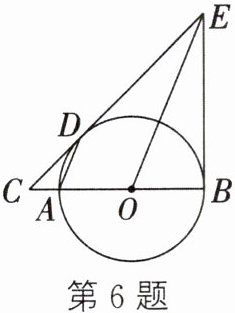
6. 如图,AB为⊙O的直径,过圆上一点D作⊙O的切线CD交BA的延长线于点C,连接AD,过点O作OE//AD,交CD于点E,连接BE.直线BE与⊙O相切吗？请判断并说明理由.

答案： 直线 BE 与⊙O 相切 理由:如图,连接 OD.
∵ CD 与⊙O 相切于点 D,
∴ ∠ODE = 90°.
∵ OE//AD,
∴ ∠ODA = ∠DOE,∠OAD = ∠BOE.
∵ OD = OA,
∴ ∠ODA = ∠OAD.
∴ ∠DOE = ∠BOE.
∵ OD = OB,OE = OE,
∴ △DOE≌△BOE.
∴ ∠ODE = ∠OBE = 90°.
∴ OB⊥BE.
∵ OB 是⊙O 的半径,
∴ 直线 BE 与⊙O 相切.

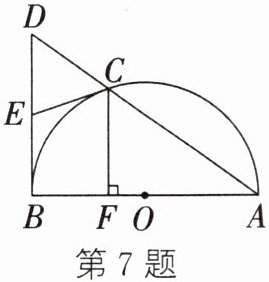
7. 如图,AB为半圆O的直径,弦AC的延长线与过点B的切线交于点D,E为BD的中点,连接CE.
(1)求证：CE是半圆O的切线；
(2)过点C作CF⊥AB,垂足为F,AC= 5,CF= 3,求半圆O的半径.

答案：
(1)连接 OC,OE,BC.
∵ BD 是半圆 O 的切线,
∴ AB⊥BD,即∠ABD = 90°.
∵ AB 是半圆 O 的直径,
∴ ∠BCA = ∠BCD = 90°.在 Rt△BCD 中,
∵ E 为 BD 的中点,
∴ CE = BE = DE.又
∵ OC = OB,OE = OE,
∴ △OCE≌△OBE.
∴ ∠OCE = ∠OBE = 90°.
∴ OC⊥CE.又
∵ OC 是半圆 O 的半径,
∴ CE 是半圆 O 的切线　
(2)在 Rt△ACF 中,
∵ AC = 5,CF = 3,
∴ AF = $\sqrt{5^2 - 3^2}$ = 4.设半圆 O 的半径为 r,则 OF = 4 - r.在 Rt△OCF 中,
∵ CF² + OF² = OC²,
∴ 3² + (4 - r)² = r²,解得 r = $\frac{25}{8}$.
∴ 半圆 O 的半径为$\frac{25}{8}$

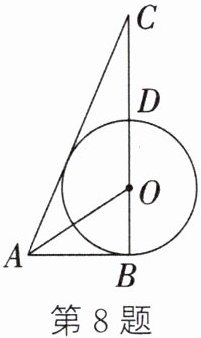
8. 如图,在△ABC中,AO平分∠BAC交BC于点O,以点O为圆心、OB为半径的⊙O与AB相切于点B,与BC相交于点D.
(1)求证：AC是⊙O的切线；
(2)若AB= 5,AC= 13,设△ABO的面积为S_1,△ABC的面积为S_2,m= $\frac{S_1}{S_2}$.求常数m的值.

答案：
(1)如图,过点 O 作 OE⊥AC,垂足为 E.
∵ 以点 O 为圆心,OB 为半径的⊙O 与 AB 相切于点 B,
∴ OB⊥AB.
∵ AO 平分∠BAC,
∴ OE = OB.
∴ OE 是⊙O 的半径.又
∵ OE⊥AC,
∴ AC 是⊙O 的切线　
(2)在 Rt△ABC 中,由勾股定理,得 BC = $\sqrt{AC^2 - AB^2}=\sqrt{13^2 - 5^2}=12$.
∵ AB,AC 与⊙O 分别相切于点 B,E,
∴ AE = AB = 5.设⊙O 的半径为 r,则 OE = OB = r,CE = AC - AE = 13 - 5 = 8,OC = BC - OB = 12 - r.在 Rt△COE 中,
∵ OC² = CE² + OE²,
∴ (12 - r)² = 8² + r²,解得 r = $\frac{10}{3}$,即 OB = $\frac{10}{3}$.
∴ m = $\frac{S_1}{S_2}=\frac{\frac{1}{2}AB\cdot OB}{\frac{1}{2}AB\cdot BC}=\frac{OB}{BC}=\frac{\frac{10}{3}}{12}=\frac{5}{18}$

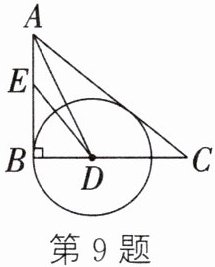
9. 如图,在Rt△ABC中,∠ABC= 90°,∠BAC的平分线交BC于点D,E为AB上一点,DE= DC,以点D为圆心,DB为半径作⊙D,AB= 10,EB= 6.
(1)求证：AC是⊙D的切线；
(2)求线段AC的长.

答案：
(1)过点 D 作 DF⊥AC 于点 F.
∵ ∠ABC = 90°,
∴ AB⊥BC.又
∵ AD 平分∠BAC,
∴ DB = DF.
∴ DF 为⊙D 的半径.又
∵ DF⊥AC,
∴ AC 是⊙D 的切线　
(2)在 Rt△BDE 和 Rt△FDC 中,$\begin{cases} DE = DC \\ DB = DF \end{cases}$,
∴ Rt△BDE≌Rt△FDC.
∴ EB = CF.
∵ AB,AF 是⊙D 的切线,
∴ AB = AF.
∴ AC = AF + CF = AB + EB = 10 + 6 = 16