《2025年金钥匙提优训练课课练九年级物理上册苏科版徐州专版》

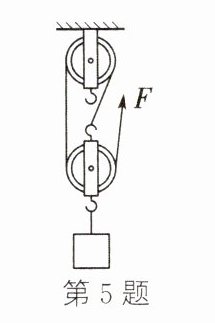
5. (2024·湖南模拟)利用如图所示的滑轮组将重为 300 N 的重物竖直匀速提升 3 m，若滑轮组的机械效率为 80%，不计绳重和摩擦，拉力 $ F = $125N，仅增大重物的重力，滑轮组的机械效率将会提高(提高/不变/降低)。

答案： 5. 125，提高。

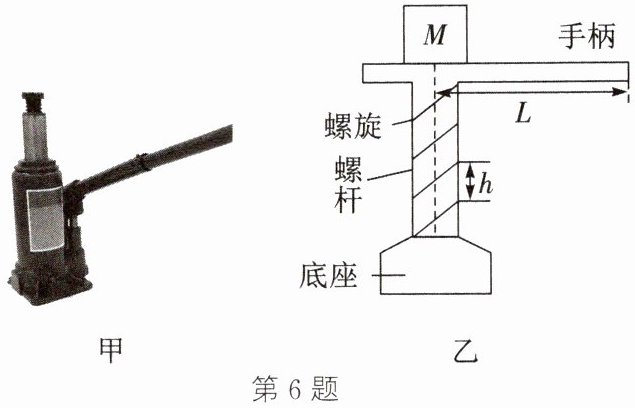
6. (2023·铜山期中)根据斜面可以省力的原理，人们在生活中发明了螺旋状的机械工具，如螺栓、螺钉、螺旋千斤顶(如图甲所示)等。螺旋千斤顶通过人力旋转手柄，使螺杆上升，从而达到将重物举起的目的。螺旋千斤顶可以省力，不可以(可以/不可以)省功。如图乙所示，使用螺旋千斤顶时，若人用始终垂直于手柄的力 $ F $，且作用点离螺杆中心的距离为 $ L $，每旋转两圈，螺杆将质量为 $ m $ 的重物上举的高度为 $ h $，则螺旋千斤顶的机械效率 $ \eta = $$\frac{mgh}{4 \pi FL}$×100%。若加润滑油，则螺旋千斤顶的机械效率增大(增大/保持不变/减小)。

答案： 6. 不可以，$\frac{mgh}{4 \pi FL}$，增大。

7. (2025·沈阳于洪校级模拟)如图所示，在探究“滑轮组的机械效率”时，小明用一个动滑轮和一个定滑轮组成的滑轮组进行实验，实验中测得数据真实可靠，见下表：


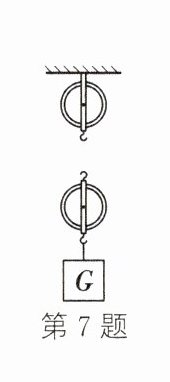
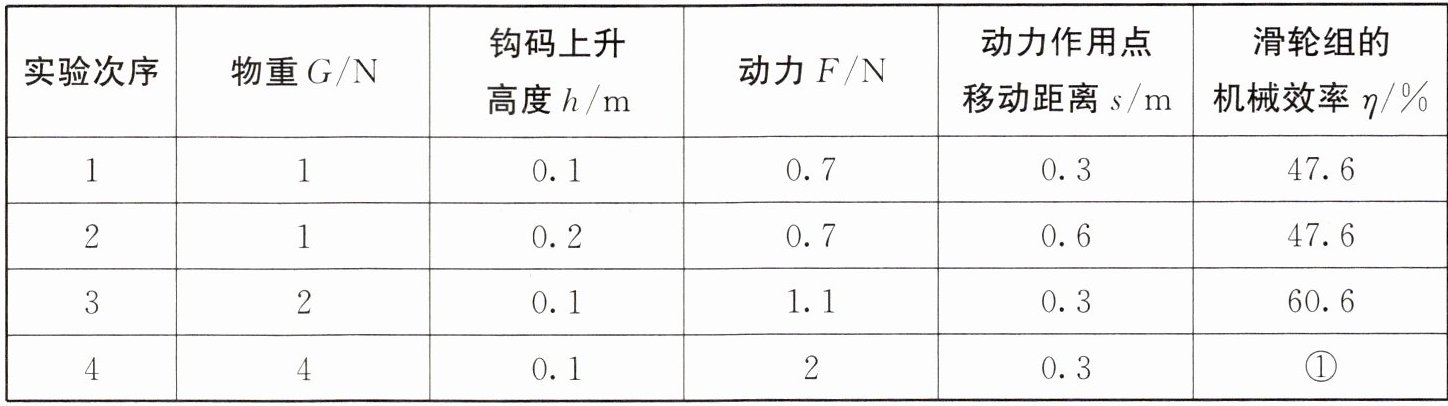
(1)请根据表中数据，在图中画出实验中滑轮组的绕绳方法。
(2)表格中编号①处数据应填66.7，此次实验做的总功是0.6J。
(3)由表中第 1、2 组数据可知，同一滑轮组的机械效率与物体被提升的高度无关。
(4)分析表中第 1、3、4 组数据，可得出实验结论：同一滑轮组匀速提升重物时，机械效率随被提升的物重的增加而增大。

答案：
7.
(1) 如图所示
(2) 66.7，0.6
(3) 物体被提升的高度
(4) 被提升的物重

8. 穿戴滑雪装备的滑雪者的总质量为 72 kg。为了帮助滑雪者登上长 200 m、高 40 m 的山坡，滑雪场沿山坡铺设了一条直雪道。在 2 min 内，用拉力将滑雪者沿此雪道由坡底匀速拉至坡顶时，雪道斜面的机械效率是 80%， $ g $ 取 10 N/kg。求：
（1）拉力对滑雪者所做的有用功。
（2）拉力对滑雪者做功的功率。
（3）滑雪者受到雪道的摩擦力。

答案： 8.
(1) 拉力对滑雪者做的有用功$W_{有用}=Gh = mgh = 72 kg × 10 N/kg × 40 m = 2.88 × 10^{4} J$。
(2) 由$\eta=\frac{W_{有用}}{W_{总}} × 100\%$得，拉力对滑雪者做的功$W_{总}=\frac{W_{有用}}{\eta}=\frac{2.88 × 10^{4} J}{80\%}=3.6 × 10^{4} J$，拉力对滑雪者做功的功率$P=\frac{W_{总}}{t}=\frac{3.6 × 10^{4} J}{2 × 60 s}=300 W$。
(3) 拉力对滑雪者所做的额外功$W_{额外}=W_{总}-W_{有用}=3.6 × 10^{4} J - 2.88 × 10^{4} J = 7.2 × 10^{3} J$，滑雪者受到雪道的摩擦力$f=\frac{W_{额外}}{s}=\frac{7.2 × 10^{3} J}{200 m}=36 N$。