《2025年金钥匙提优训练课课练九年级物理上册苏科版徐州专版》

4. (2023·新沂段考)如图所示，斜面长5m，小明用绳子沿与水平面成30°角的斜面将重为300N的木块由斜面底端匀速拉到顶端，拉力大小为240N，绳重不计。求：
(1) 斜面对木块的摩擦力大小。
(2) 斜面的机械效率。

答案： （1）斜面与水平面成$30^{\circ}$的角，$h = \frac{1}{2}L = \frac{1}{2} × 5\ m = 2.5\ m$，$W_{有用} = Gh = 300\ N × 2.5\ m = 750\ J$，总功$W_{总} = FL = 240\ N × 5\ m = 1200\ J$，$W_{额外} = W_{总} - W_{有用} = 1200\ J - 750\ J = 450\ J$，$f = \frac{W_{额外}}{L} = \frac{450\ J}{5\ m} = 90\ N$ （2）机械效率$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{750\ J}{1200\ J} × 100\% = 62.5\%$

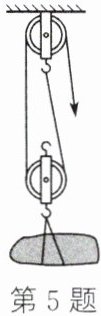
5. (2024·常州模拟)小明家新买的房子准备装修，为了将水泥从地面运送上楼，他安装了一个滑轮组(如图所示)，小明站在楼下每次用300N的力将一袋50kg的水泥提升5m，不计绳重和摩擦，g取10N/kg，则：
(1) 小明用此滑轮组运送一袋水泥上楼时的机械效率是多大？
(2) 若小明的体重为600N，小明每次最多能运送几袋水泥？此时滑轮组的机械效率最大可以达到多少？(结果精确到0.1%)

答案： （1）一袋水泥所受的重力$G = mg = 50\ kg × 10\ N/kg = 500\ N$。
由图可知$n = 2$，滑轮组的机械效率$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{Gh}{Fs} × 100\% = \frac{Gh}{Fnh} × 100\% = \frac{G}{nF} × 100\% = \frac{500\ N}{2 × 300\ N} × 100\% \approx 83.3\%$
（2）因为不计绳重和摩擦时$F = \frac{1}{n}(G + G_{动})$，所以动滑轮的重力$G_{动} = nF - G = 2 × 300\ N - 500\ N = 100\ N$。小明的体重为$600\ N$，则绳子自由端的最大拉力$F' = G_{人} = 600\ N$，此滑轮组能提升的最大物重$G' = nF' - G_{动} = 2 × 600\ N - 100\ N = 1100\ N$，小明每次最多能运送水泥的袋数$n' = \frac{G'}{G} = \frac{1100\ N}{500\ N} \approx 2$，此时滑轮组的最大机械效率$\eta' = \frac{W_{有用}'}{W_{总}'} × 100\% = \frac{W_{有用}'}{W_{有用}' + W_{额外}'} × 100\% = \frac{G''h}{G''h + G_{动}h} × 100\% = \frac{G''}{G'' + G_{动}} × 100\% = \frac{2 × 500\ N}{2 × 500\ N + 100\ N} × 100\% \approx 90.9\%$

6. (2024·六安霍邱期中)建筑工地上，施工人员用起重机吊臂上的滑轮组吊起建筑材料，可简化成如图甲所示的滑轮组。每个滑轮等重，不计绳重及摩擦，物重从G$_物$=2000N开始逐渐增加，直到绳子被拉断，每次以0.15m/s匀速拉动绳子将物体提升同样的高度。图乙记录了在此过程中滑轮组的机械效率随物体重力的增加而变化的图像。求：
(1) 每个滑轮所受重力。
(2) 绳子能承受的最大拉力。
(3) 当滑轮组的机械效率为80%时，起重机的功率。

答案： （1）由图乙可知当滑轮组提起$2000\ N$物体时，机械效率为$50\%$，不计绳重和摩擦，根据$\eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{W_{有用}}{W_{有用} + W_{额外}} × 100\% = \frac{Gh}{Gh + G_{动}h} × 100\% = \frac{G}{G + G_{动}} × 100\%$可知，动滑轮重$G_{动} = \frac{G}{\eta} - G = \frac{2000\ N}{50\%} - 2000\ N = 2000\ N$
（2）由图甲可知，$n = 3$，由图乙可知物体在$16000\ N$时绳子断了，不计绳重和摩擦，绳子能承受的最大拉力$F_{大} = \frac{1}{n}(G' + G_{动}) = \frac{1}{3} × (16000\ N + 2000\ N) = 6000\ N$ （3）当滑轮组的机械效率为$80\%$时，不计绳重和摩擦，根据$\eta' = \frac{W_{有用}'}{W_{总}'} × 100\% = \frac{W_{有用}'}{W_{有用}' + W_{额外}'} × 100\% = \frac{G''h}{G''h + G_{动}h} × 100\% = \frac{G''}{G'' + G_{动}} × 100\%$可知，物重$G'' = \frac{\eta'G_{动}}{1 - \eta'} = \frac{80\% × 2000\ N}{1 - 80\%} = 8000\ N$，不计绳重和摩擦，此时拉力$F' = \frac{1}{n}(G'' + G_{动}) = \frac{1}{3} × (8000\ N + 2000\ N) = \frac{10000}{3}\ N$，起重机的功率$P = \frac{W}{t} = \frac{F's}{t} = F'v = \frac{10000}{3}\ N × 0.15\ m/s = 500\ W$