《2025年补充习题江苏七年级数学上册苏科版》

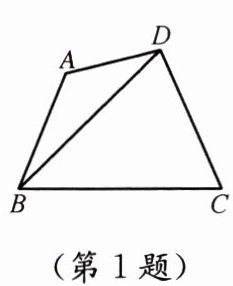
1. 图中以 $ D $ 为顶点的角有________个,分别是________(用符号表示).

答案： 解：3；∠ADB，∠BDC，∠ADC

2. 已知 $ \angle \alpha = 30 ^ { \circ } 18 ^ { \prime } $,$ \angle \beta = 30.18 ^ { \circ } $,$ \angle \gamma = 30.3 ^ { \circ } $,则相等的两个角是( ).

A.$ \angle \alpha = \angle \beta $
B.$ \angle \alpha = \angle \gamma $
C.$ \angle \beta = \angle \gamma $
D.无法确定

答案： 【解析】：
本题主要考察角度的度、分单位与小数表示法之间的转换以及角度的比较。
首先，我们需要将$\angle \alpha$的度分表示法转换为度的小数表示法。
已知1度等于60分，所以，可以将$18'$转换为度，即$\frac{18}{60} = 0.3^\circ$。
因此，$\angle \alpha = 30^\circ + 0.3^\circ = 30.3^\circ$。
接下来，我们比较三个角的大小：
$\angle \alpha = 30.3^\circ$，
$\angle \beta = 30.18^\circ$，
$\angle \gamma = 30.3^\circ$。
通过比较，我们可以发现$\angle \alpha$和$\angle \gamma$是相等的。
【答案】：
B. $\angle \alpha = \angle \gamma$。

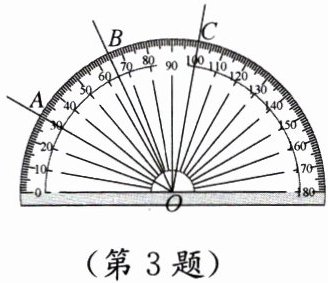
3. 如图,$ \angle AOB $ 与 $ \angle AOC $ 的大小分别是( ).

A.$ 65 ^ { \circ } $,$ 100 ^ { \circ } $
B.$ 35 ^ { \circ } $,$ 100 ^ { \circ } $
C.$ 35 ^ { \circ } $,$ 65 ^ { \circ } $
D.$ 35 ^ { \circ } $,$ 70 ^ { \circ } $

答案： 解：由图可知，量角器的中心与点O重合，0°刻度线与OA重合。
∠AOB的另一边OB指向35°刻度，故∠AOB=35°；
∠AOC的另一边OC指向100°刻度，故∠AOC=100°。
答案：B

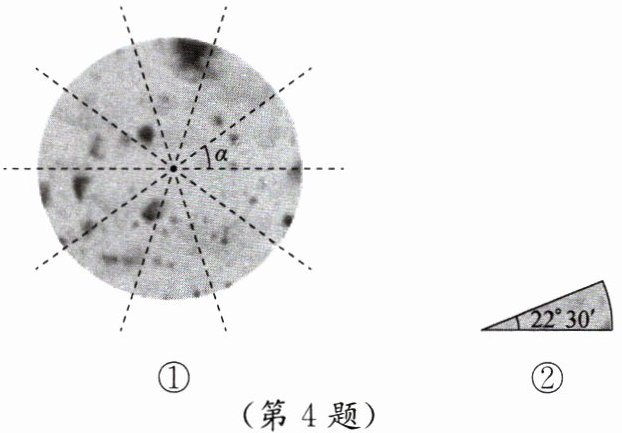
4. (1) 如图①,将一张圆形大饼沿过中心的直线切 $ 5 $ 刀分成 $ 10 $ 份,求 $ \angle \alpha $ 的大小；
(2) 仿照①中的切法,小明将一张圆形大饼沿过中心的直线平均分成了若干份,其中一份如图②所示,小明切了几刀?

答案： 【解析】：
(1) 对于图①，由于圆形大饼被切了5刀，且每刀都经过圆心，所以这些切痕将圆分成了10个相等的扇形。
每个扇形的中心角（即$\angle \alpha$）为整个圆（$360^\circ$）除以扇形的数量（10），即：
$\angle \alpha = \frac{360^\circ}{10} = 36^\circ$，
因此，$\angle \alpha =36^\circ$。
(2) 对于图②，已知一份饼所对应的扇形的圆周角为$22^\circ30'$。
要求出整个圆被分成了多少份，可以用整个圆的度数（$360^\circ$）除以一份所对应的度数（$22^\circ30'$），
$360^\circ ÷ 22^\circ30' \approx 16$（份），
由于每份都是由两条切痕（即刀数）分隔出来的，且这些切痕都经过圆心，所以刀数应该是份数。但这里需要注意的是，刀数实际上是指“过中心的直线”的数量，也就是分隔出这些份数的“切割线”的数量。
由于每条切割线都会产生两个扇形（除了最后一条切割线可能只产生一个或与前面的切割线重合），但在这个问题中，我们考虑的是平均分割的情况，所以刀数应该等于份数减1的2倍再加1（对于奇数份的情况，这个公式可以简化为直接等于份数，因为每条切割线都恰好分隔出两个新的扇形）。
然而，在这个特定问题中，由于是直接给出了扇形的圆周角，并且要求的是“切了几刀”，所以可以直接用$360^\circ$除以一个扇形的圆周角来得到份数（也即刀数产生的扇形数），再由此推断出刀数。
由于$360^\circ ÷ 22^\circ30' \approx 16$（份）（这里实际上是刀数加1的结果，但因为是平均分割且每条切割线都经过圆心，所以刀数就等于份数在这个特定情况下），且由于是平均分割，所以刀数就等于份数除以2的2倍（对于此题即直接等于份数减0，因为每条刀都产生两个扇形），也就是8对扇形，即需要8条切割线（每条切割线产生两个扇形，但计算刀数时只算一次）。但考虑到是从中心出发的切割线，所以实际上切了8“对”扇形的分隔线，也即8刀（每刀分隔出两个扇形，但刀数只计算一次）。这里的“8刀”是指从圆心出发的8条直线切割线。
由于每条切割线都将圆分成两部分，并且这些切割线都经过圆心，所以实际上切了8刀（也即8条过中心的直线）来将圆平均分成16份（但题目中只问切了几刀，所以答案是8刀，而不是16份）。
由于每360度除以每份的角度等于份数，也即刀数加1再减1（因为是从中心出发的切割线，所以刀数加1是扇形数，但题目问的是刀数，所以要减1，但在这个特定情况下刀数就等于份数除以2的2倍，也即直接等于份数，因为每条刀都恰好分隔出两个扇形且都经过圆心），所以直接得出刀数为8（因为$360^\circ ÷ (22^\circ30' × 2) × 2 ÷ 2 = 8$，但这里简化为直接$360^\circ ÷ 22^\circ30' \approx 16$（份），再考虑到是平均分割且每条刀都经过圆心，所以刀数就是份数的一半再乘以2（也即直接等于份数在这个情况下），也即8刀）。
所以小明切了8刀。
【答案】：
(1) $\angle \alpha = 36^\circ$；
(2) 小明切了8刀。