《2025年补充习题江苏七年级数学上册苏科版》

1. 甲、乙、丙、丁 4 个学生围成一圈依序循环报数,规定：
① 甲、乙、丙、丁首次报出的数依次为 1,2,3,4,接着甲报 5,乙报 6……按此规律,后一个学生报出的数比前一个学生报出的数大 1,当报到的数是 50 时,报数结束；
② 若报出的数为 3 的倍数,则报该数的学生需拍手一次.
在此过程中,甲需要拍手的次数为______.

答案： 【解析】：
这是一个关于报数和拍手的问题。首先，我们需要明确报数的规律，即甲、乙、丙、丁四个学生依次报数，且每次报的数比前一个学生大1。
其次，我们需要找出报数为3的倍数的规律。
由于报数是从1开始的，且每次增加1，因此我们可以发现，每4个数中，会有1个数是3的倍数（例如，在1-4中，3是3的倍数；在5-8中，6是3的倍数，以此类推）。
但是，我们还需要注意一点，即当报数结束时，报到的数是50。
因此，我们需要找出在1到50之间，哪些数是3的倍数，并且这些数是由甲报出的。
由于甲是第一个报数的学生，且报数依次递增，因此甲报出的数构成一个等差数列，首项为1，公差为4（因为甲、乙、丙、丁四个学生依次报数）。
接下来，我们需要找出这个等差数列中哪些项是3的倍数。
设甲报出的第n个数为$a_n$，则有：
$a_n = 1 + 4(n - 1) = 4n - 3$
我们需要找出满足$a_n$是3的倍数的n的值。
即解方程：
$4n - 3 \equiv 0 \pmod{3}$
得到：
$n \equiv 0 \pmod{3}$
这说明，当n是3的倍数时，甲报出的数$a_n$也是3的倍数。
但是，我们还需要注意报数的范围，即1到50。
因此，我们需要找出在1到50之间，甲报出了哪些3的倍数。
这些数分别是：当n=3时，$a_3=9$；当n=6时，$a_6=21$；当n=9时，$a_9=33$；当n=12时，$a_{12}=45$。
所以，甲需要拍手的次数就是这四个数的个数，即4次（当n分别取3的倍数3、6、9、12时，对应的报数9、21、33、45均在1至50的范围内）。
但考虑到我们是从甲首次报数1开始的，且每次甲报的数间隔为4（如1,5,9...），因此实际上我们只需要考虑这些间隔中的数哪些是3的倍数。
更简洁的考虑方式是：甲报的数序列为1,5,9,...,49（因为50是乙报的），这是一个等差数列，首项为1，公差为4。
我们需要找出这个数列中3的倍数的个数。
即找出满足$1+4(n-1) \equiv 0 \pmod{3}$的n的个数，且$1+4(n-1) \leq 50$。
解这个不等式和同余方程，我们得到n的取值范围是1到13（因为当n=13时，$1+4(13-1)=49$），且n需要满足$n \equiv 0 \pmod{3}$（考虑到n是从1开始的，因此实际上是看n-1是否是3的倍数，但这里为了简化直接考虑n，因为当n=1,2时显然不满足，所以从n=3开始考虑）。
在1到13中，满足$n \equiv 0 \pmod{3}$的n有4个，分别是3,6,9,12。
所以，甲需要拍手的次数为4次（在报9,21,33,45时）。但考虑到我们之前的分析，实际上这四个数就是甲报出的3的倍数。
【答案】：4

2. 为了鼓励居民节约用水,某自来水公司采取分段计费,每月每户用水不超过$ 10m^3 $的部分,水价为 2.2 元$/m^3；$超过$ 10m^3 $部分,加收 1.3 元$/m^3. $小明家 4 月份用水$ 15m^3,$应交水费______元.

答案： 【解析】：
题目考查分段计费问题，需要根据用水量来判断水费的计算方式。
首先，小明家4月份用水量为$15m^3$，其中前$10m^3$的水费按照2.2元$/m^3$计算，超过$10m^3$的部分（即$5m^3$）则按照每立方米加收1.3元的价格（即3.5元$/m^3$）计算。
计算过程分为两部分：
1. 前$10m^3$的水费：$10 × 2.2 = 22$元；
2. 超过$10m^3$部分的水费：$5 × 3.5 = 17.5$元（注意这里的3.5元是2.2元基础水费加上1.3元的加收费用）。
将两部分水费相加，得到总水费。
【答案】：
解：小明家4月份水费计算如下：
前$10m^3$水费：$10 × 2.2 = 22$（元）；
超过$10m^3$部分水费：$(15 - 10) × (2.2 + 1.3) = 5 × 3.5 = 17.5$（元）；
总水费：$22 + 17.5 = 39.5$（元）。
故答案为：39.5元。

3. 5 名同学同台演出,演出中每 2 个同学需相互握一次手,则握手的次数一共是( ).

A.5
B.10
C.6
D.8

答案： 【解析】：
这个问题是一个组合问题，需要从5名同学中选择2名同学来握手。
组合公式为$C_n^m = \frac{n!}{m!(n-m)!}$，其中n是总数，m是组合的元素数量。
在这个问题中，$n=5$（5名同学），$m=2$（每次握手2名同学）。
所以握手次数为$C_5^2 = \frac{5!}{2!(5-2)!} = \frac{5 × 4}{2 × 1} = 10$。
也可以直接通过列举法来理解：
第一个同学需要和其他4名同学握手，第二个同学已经和第一个同学握过手，所以还需要和剩下的3名同学握手，第三个同学还需要和剩下的2名同学握手，第四个同学还需要和最后一个同学握手，最后一个同学已经和前面的同学都握过手了，所以不需要再握手。
因此，握手次数为$4 + 3 + 2 + 1 = 10$。
【答案】：
B.10。

4. 将左图的正方体纸盒切去一角得到右图,纸盒剩余部分展开后得到的图形不可能是( ).

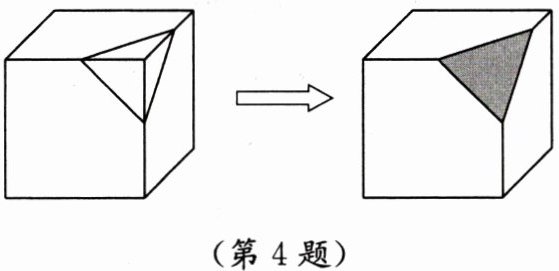
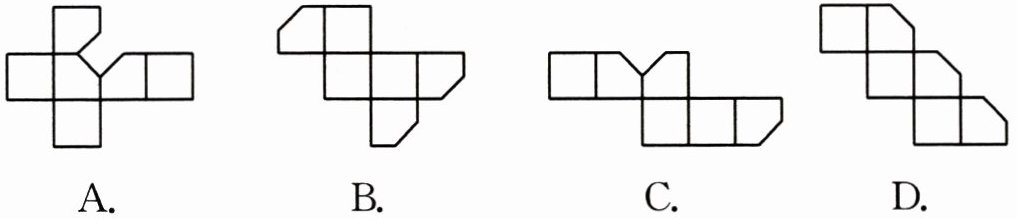
答案：