《2025年本土假期作业巩固训练八年级数学》

1. 如图,在平行四边形 $ABCD$ 中,按下列条件得到的四边形 $EFGH$ 不一定是平行四边形的是(C)

答案： 【解析】：本题可根据平行四边形的判定定理，逐一分析每个选项中四边形$EFGH$是否为平行四边形。
选项A：
已知$EF\perp BC$，$GH\perp AD$，因为四边形$ABCD$是平行四边形，所以$AD// BC$，那么$EF// GH$。
又因为$EF$和$GH$都垂直于平行线$AD$与$BC$，所以$EF = GH$（平行线间的距离处处相等）。
一组对边平行且相等的四边形是平行四边形，所以四边形$EFGH$是平行四边形。
选项B：
因为$E$，$F$，$G$，$H$是四边形各边的中点，连接四边形各边中点所得的四边形是平行四边形（三角形中位线定理的推论：顺次连接四边形各边中点所得的四边形是平行四边形），所以四边形$EFGH$是平行四边形。
选项C：
虽然$AF$，$BH$，$CH$，$DF$是角平分线，但仅根据这些条件不能直接得出四边形$EFGH$的对边平行且相等或者对角相等或者对角线互相平分等判定平行四边形的条件，所以四边形$EFGH$不一定是平行四边形。
选项D：
因为$EG$，$FH$是过对角线交点的两条线段，在平行四边形$ABCD$中，对角线互相平分，根据平行四边形的性质及对角线的性质可以推出四边形$EFGH$的对角线互相平分。
对角线互相平分的四边形是平行四边形，所以四边形$EFGH$是平行四边形。
【答案】：C

2. 如图1,$□ ABCD$ 中,$AD ＞ AB$,$\angle ABC$ 为锐角. 要在对角线 $BD$ 上找点 $N$,$M$,使四边形 $ANCM$ 为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案是( A )
A.甲、乙、丙都是
B.只有甲、乙才是
C.只有甲、丙才是

D.只有乙、丙才是

答案： 【解析】：
首先，分析题目给出的条件：
在平行四边形$ABCD$中，$AD \gt AB$，$\angle ABC$为锐角。
目标是在对角线$BD$上找到点$M$和$N$，使得四边形$ANCM$成为平行四边形。
接下来，逐一分析三种方案：
方案甲：
连接$AC$，作$AC$的垂直平分线交$BD$于点$O$。
由于$O$是$AC$的中点，根据平行四边形的对角线性质，$AN$和$CM$都将通过$O$点，并且$AN=CM$，$AN// CM$。
因此，四边形$ANCM$是平行四边形。
所以，方案甲是正确的。
方案乙：
以$BD$为直径作圆，交$AC$于点$O$（由于$BD$是平行四边形的对角线，它一定会与$AC$相交于中点$O$，但此处作为方案的一部分，我们假设这是通过作图得到的）。
连接$AO$并延长交$BD$于点$N$，同样连接$CO$并延长交$BD$于点$M$。
由于$O$是$AC$的中点，且$AN$和$CM$都经过$O$点，并且由于圆的性质，$\angle AON = \angle COM$（对顶角与圆周角的关系，或者通过证明三角形全等来得到）。
又因为$AO=CO$（$O$是$AC$的中点），且$\angle ANO = \angle CMO$（都为直角，因为$AN$和$CM$都是圆的半径所对的圆周角，或者通过证明与$BD$垂直来得到）。
所以，根据三角形的全等性质，$\triangle AON \cong \triangle COM$，从而$AN=CM$，$AN// CM$。
因此，四边形$ANCM$是平行四边形。
但需要注意的是，这里的证明过程稍微复杂一些，且依赖于圆的性质和三角形的全等。然而，就方案本身而言，它是正确的，因为它确实能够找到满足条件的$M$和$N$。
方案丙：
连接$AC$，作线段$AC$的平行线，分别交$AB$，$CD$于点$E$，$F$。
连接$BD$，交$EF$于点$O$。
过$O$作$AN// CM$，分别交$AD$，$BC$于点$N$，$M$。
由于$EF// AC$，根据平行线的性质，可以得到一系列的相似三角形和比例关系。
又因为$AN// CM$且$AN$，$CM$都在平行四边形$ABCD$的内部，所以可以通过证明三角形全等或相似来得到$AN=CM$。
同时，由于$AN$和$CM$都平行于$AC$（或者通过$EF$平行于$AC$来间接证明），所以$AN// CM$。
因此，四边形$ANCM$是平行四边形。
所以，方案丙也是正确的。
综上所述，三种方案都是正确的。
【答案】：A。

3. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形 $ABCD$,其中一张纸条在转动过程中,下列结论一定成立的是(D)
A.四边形 $ABCD$ 周长不变
B.$AD = CD$
C.四边形 $ABCD$ 面积不变
D.$AD = BC$

答案： 【解析】：
本题主要考查平行四边形的性质。
首先，由于两张纸条的对边平行，所以它们交叉叠放形成的四边形$ABCD$是一个平行四边形。
对于选项A：四边形$ABCD$的周长会随着纸条的转动而发生变化。因为当纸条转动时，重合的部分会改变，从而导致四边形的边长发生变化。所以选项A是错误的。
对于选项B：在平行四边形$ABCD$中，对边相等，即$AB = CD$和$AD = BC$，但并不能保证$AD = CD$。所以选项B是错误的。
对于选项C：四边形$ABCD$的面积也会随着纸条的转动而发生变化。因为面积是由基边和高决定的，当纸条转动时，高会发生变化，从而导致面积的变化。所以选项C是错误的。
对于选项D：由于$ABCD$是平行四边形，根据平行四边形的性质，对边相等，即$AD = BC$。这个性质是平行四边形固有的，不会因为纸条的转动而改变。所以选项D是正确的。
【答案】：
D

4. 如图,等边三角形 $ABC$ 是一块周长为 $12$ 的草坪,点 $P$ 是草坪内的任意一点,过点 $P$ 有三条小路 $PD$,$PE$,$PF$,且满足 $PD// AC$,$PE// AB$,$PF// BC$,则三条小路的总长度为(C)
A.$12$
B.$8$
C.$4$

D.$3$

答案： 解：
∵△ABC是等边三角形，周长为12，
∴AB=BC=AC=4，∠A=∠B=∠C=60°。
∵PD//AC，PE//AB，PF//BC，
∴四边形ADPF、四边形BEPD是平行四边形，
∴PD=AF，PE=BD。
∵PF//BC，PD//AC，
∴∠PFD=∠C=60°，∠PDF=∠A=60°，
∴△PDF是等边三角形，
∴PF=DF。
∴PD+PE+PF=AF+BD+DF=AB=4。
答案：C

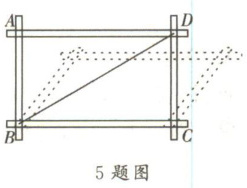
5. 如图,为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架 $ABCD$,然后向右拉动框架,给出如下的判断：① 四边形 $ABCD$ 为平行四边形；② 对角线 $BD$ 的长度不变；③ 四边形 $ABCD$ 的面积不变；④ 四边形 $ABCD$ 的周长不变. 其中所有正确的结论是(B)


A.①②
B.①④
C.①②④
D.①③④

答案： 【解析】：
首先，我们分析题目中的每一个判断：
① 四边形$ABCD$为平行四边形：由于题目描述的是用四根木条钉成的矩形框架，矩形是特殊的平行四边形，即使框架变形，只要四根木条的长度不变且相对位置保持两两平行，它仍然是一个平行四边形。所以①正确。
② 对角线$BD$的长度不变：在矩形变为一般平行四边形的过程中，对角线的长度是会发生变化的。可以通过几何作图或向量分析来证明这一点。因此，②错误。
③ 四边形$ABCD$的面积不变：平行四边形的面积是由其底和高决定的。在拉动过程中，虽然底的长度不变，但高（即与底垂直的距离）会发生变化，因此面积也会变化。所以③错误。
④ 四边形$ABCD$的周长不变：由于四根木条的长度是固定的，所以无论框架如何变形，其周长（即四根木条长度的总和）都不会改变。因此，④正确。
综上所述，正确的结论是①和④。
【答案】：B.①④。

6. 如图,$\triangle ABC$ 绕边 $AC$ 的中点 $O$ 顺时针旋转 $180^{\circ}$. 小淇发现,旋转后的 $\triangle CDA$ 与 $\triangle ABC$ 构成平行四边形,并推理如下：
点 $A$,$C$ 分别转到了点 $C$,$A$ 处,
而点 $B$ 转到了点 $D$ 处,
$\because CB = AD$,
$\therefore$ 四边形 $ABCD$ 是平行四边形.
小明为保证小淇的推理更严谨,想在“$\because CB = AD$,”和“$\therefore$ 四边形…”之间作补充,下列正确的是(A)

A.应补充：且 $AB = CD$
B.应补充：且 $AB// CD$
C.应补充：且 $OA = OC$
D.嘉淇推理严谨,不必补充

答案： 解：A. 应补充：且 $AB = CD$
理由：由旋转性质知，$\triangle ABC \cong \triangle CDA$，则 $CB = AD$ 且 $AB = CD$。根据“两组对边分别相等的四边形是平行四边形”，需补充 $AB = CD$ 使推理严谨。
答案：A