《2025年本土假期作业巩固训练八年级数学》

2. 如图,在一次“寻宝”游戏中,寻宝人找到了如图所示的两个标志点$A(-1,-3)$,$B(-2,-2)$,则“宝藏”点$C$的位置是 (D)
A.$(-3,-3)$
B.$(1,1)$
C.$(-2,-3)$
D.$(-2,-1)$

答案： 【解析】：
本题可根据点$A$、$B$的坐标确定平面直角坐标系中坐标轴的单位长度，进而确定“宝藏”点$C$的位置。
1. 首先，根据点$A(-1,-3)$和点$B(-2,-2)$的坐标，在平面直角坐标系中确定坐标轴的单位长度。
点$A$的横坐标为$-1$，纵坐标为$-3$；点$B$的横坐标为$-2$，纵坐标为$-2$。
观察坐标系中$A$、$B$两点的位置，结合其坐标可知，坐标系中每一小格代表一个单位长度。
2. 然后，根据坐标系中每一小格代表一个单位长度，确定点$C$的坐标。
从图中可以看出，点$C$的横坐标对应的数值为$-2$，纵坐标对应的数值为$-1$。
所以点$C$的坐标为$(-2,-1)$。
【答案】：D

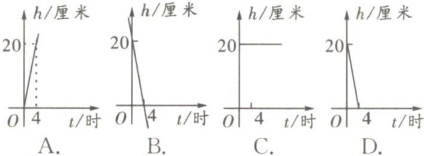
3. 一支蜡烛长 20 厘米,点燃后每小时燃烧 5 厘米,燃烧时剩下的高度$h$(厘米)与燃烧时间$t$(时)的函数关系的图象是 (B)

答案： 【解析】：
首先，根据题目描述，蜡烛的初始高度是20厘米，即当$t=0$时，$h=20$。
接着，蜡烛每小时燃烧5厘米，因此燃烧时间$t$小时后，蜡烛剩下的高度$h$可以表示为：
$h = 20 - 5t$，
这是一个一次函数，其图像是一条直线。
由于蜡烛的长度不能为负，因此当$h=0$时，可以求出蜡烛完全燃烧所需的时间：
$0 = 20 - 5t$，
$t = 4$，
所以，图像是一条从$(0,20)$出发，到$(4,0)$结束的线段。
根据这些信息，可以在草稿纸上画出这条线段，然后与选项进行对比。
通过对比，可以发现只有选项B的图像符合描述：一条从$(0,20)$出发，斜向下到$(4,0)$结束的线段。
【答案】：B。

4. 已知点$M(a,b)$在第二象限,点$M到x轴的距离等于它到y$轴距离的 2 倍,且点$M$到两坐标轴的距离之和为 9,则点$M$的坐标为$(-3, 6)$。

答案： 【解析】：
本题考查了坐标系的性质以及一元一次方程组的应用。
首先，由于点$M(a,b)$在第二象限，根据坐标系的性质，我们知道第二象限的点横坐标小于0，纵坐标大于0，即 $a ＜ 0$，$b ＞ 0$。
接着，根据题目条件“点$M$到$x$轴的距离等于它到$y$轴的距离的2倍”，我们可以得出：$b = 2(-a)$，即 $b = -2a$。
再根据题目条件“点$M$到两坐标轴的距离之和为9”，我们可以得出：$|-a| + |b| = 9$。
由于 $a ＜ 0$，$b ＞ 0$，所以 $|-a| = -a$，$|b| = b$，代入上式得：$-a + b = 9$。
现在我们得到了一个包含 $a$ 和 $b$ 的方程组：
$\begin{cases}b = -2a \\-a + b = 9\end{cases}$
解这个方程组，我们可以得到 $a = -3$，$b = 6$。
因此，点$M$的坐标为 $(-3, 6)$。
【答案】：
$(-3, 6)$

5. 某工程队正在对一湿地公园进行绿化,中间休息了一段时间,已知绿化面积$S(m^2)与工作时间t(h)$的函数关系的图象如图所示,则休息后工程队每小时绿化面积为____$m^2$。

50

答案： 解：由图象可知，休息前工作时间为2小时，绿化面积为100m²；休息后从第3小时开始到第6小时结束，工作时间为6-3=3小时，绿化面积从100m²增加到250m²，增加了250-100=150m²。
休息后每小时绿化面积为150÷3=50m²。
50

专题 3 一次函数的图象与性质
知识清单
1. 若两个变量$x$，$y$间的对应关系可以表示成$y = kx + b$（$k$，$b$为常数，$k\neq 0$）的形式，则称$y$是$x$的一次函数。特别地，当$b = 0$时，称$y$是$x$的正比例函数。
2. 一次函数$y = kx + b$的图象是一条直线，与$x$轴的交点坐标为$\left(-\dfrac{b}{k},0\right)$，与$y$轴的交点坐标为$(0,b)$。当$k\gt 0$时，$y$随$x$的增大而增大；当$k\lt 0$时，$y$随$x$的增大而减小。
3. 若两直线平行，则它们的$k$值相等。由一次函数$y = kx + b$的图象向上平移$h(h\gt 0)$个单位，可得一次函数$y = kx + (b + h)$的图象；由一次函数$y = kx + b$的图象向下平移$h(h\gt 0)$个单位，可得一次函数$y = kx + (b - h)$的图象。简记为“上加下减”。

答案： 解：2. $\left(-\dfrac{b}{k},0\right)$；$(0,b)$；增大；减小
3. 它们的$k$值相等

例 1 已知$y= (m - 2)x^{|m| - 1} + 4$是一次函数,则$m$的值为 (  )

A.$1$
B.$2$
C.$-2$
D.$\pm 2$

答案： 【解析】：
根据一次函数的定义，一次函数的形式为$y=kx+b$，其中$k$是常数且$k \neq 0$。
所以对于给定的函数$y= (m - 2)x^{|m| - 1} + 4$来说，需要满足两个条件才能使其为一次函数：
$|m| - 1 = 1$，使得$x$的指数为1，即函数为一次函数形式；
$m - 2 \neq 0$，确保$x$的系数不为0。
解第一个方程$|m| - 1 = 1$，得到$|m| = 2$，所以$m = 2$或$m = -2$。
但由第二个条件$m - 2 \neq 0$，排除$m = 2$，所以$m = -2$。
【答案】：
C. $-2$

例 2 若$b\gt 0$,则一次函数$y = -x + b$的图象大致是 (  )

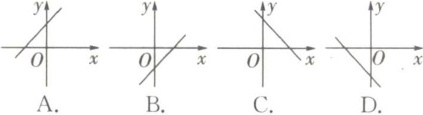
答案： 【解析】：
题目考察了一次函数$y = kx + b$的图象与$k$，$b$符号的关系。
当$k \gt 0$时，函数图象是从左下到右上的直线，必经过一、三象限，$y$随$x$的增大而增大；
当$k \lt 0$时，函数图象是从左上到右下的直线，必经过二、四象限，$y$随$x$的增大而减小。
同时，$b$的值决定了直线与$y$轴的交点位置：
当$b \gt 0$时，直线与$y$轴正半轴相交；
当$b = 0$时，直线过原点；
当$b \lt 0$时，直线与$y$轴负半轴相交。
对于本题，已知$b \gt 0$，且函数为$y = -x + b$，其中$k = -1 \lt 0$。
因此，根据一次函数的性质，图象将经过第二、四象限，并且与$y$轴的正半轴相交。
对比选项，只有C选项符合这一条件。
【答案】：C

例 3 关于一次函数$y = -3x - 2$,下列说法错误的是 (  )

A.函数图象与$y轴的交点坐标为(0,-2)$
B.函数图象经过二、三、四象限
C.函数图象与$x轴的交点在x$轴的负半轴
D.$y的值随x$的值的增大而增大

答案： 【解析】：
本题主要考察一次函数图象上点的坐标特征以及一次函数的性质。
A选项：考察的是一次函数图象与坐标轴的交点。对于函数$y = -3x - 2$，当$x=0$时，$y=-2$，所以函数图象与$y$轴的交点坐标为$(0,-2)$，A选项正确。
B选项：考察的是一次函数图象经过的象限。一次函数$y = kx + b$，当$k＜0$且$b＜0$时，函数图象经过二、三、四象限。对于函数$y = -3x - 2$，$k=-3＜0$，$b=-2＜0$，所以B选项正确。
C选项：考察的是一次函数图象与$x$轴的交点。对于函数$y = -3x - 2$，当$y=0$时，$x=-\frac{2}{3}$，所以函数图象与$x$轴的交点坐标为$\left(-\frac{2}{3},0\right)$，在$x$轴的负半轴上，C选项正确。
D选项：考察的是一次函数的增减性。一次函数$y = kx + b$，当$k＜0$时，$y$的值随$x$的增大而减小。对于函数$y = -3x - 2$，$k=-3＜0$，所以$y$的值随$x$的增大而减小，D选项错误。
【答案】：
D