《2025年本土假期作业巩固训练八年级数学》

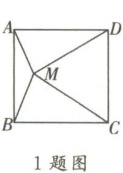
1. 已知:如图,M 是正方形 ABCD 内的一点,且 MC= MD= AD,则∠AMB 的度数为 (D)

A.120°
B.135°
C.145°
D.150°

答案： 解：
∵四边形ABCD是正方形，
∴AD=CD，∠ADC=∠BCD=90°。
∵MC=MD=AD，
∴MD=MC=CD，
∴△MDC是等边三角形，
∴∠MDC=∠MCD=60°，
∴∠ADM=∠ADC - ∠MDC=90° - 60°=30°。
∵AD=MD，
∴∠DAM=∠DMA=(180° - ∠ADM)/2=(180° - 30°)/2=75°，
同理∠BCM=90° - 60°=30°，∠CBM=∠CMB=75°。
∵∠DAB=∠CBA=90°，
∴∠MAB=∠DAB - ∠DAM=90° - 75°=15°，
∠MBA=∠CBA - ∠CBM=90° - 75°=15°，
∴∠AMB=180° - ∠MAB - ∠MBA=180° - 15° - 15°=150°。
答案：D

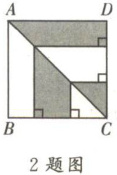
2. 如图,正方形 ABCD 的边长为 4 cm,则图中阴影部分的面积为 (B)
$A. 6 cm^2 B. 8 cm^2 C. 16 cm^2 D. $不能确定

答案： 【解析】：
本题主要考查正方形的性质以及对称性质的应用。
首先，观察图形，可以看到阴影部分是正方形的一半减去一个等腰直角三角形。然而，由于正方形的对称性和等腰直角三角形的性质，我们可以发现阴影部分实际上占据了正方形面积的一半。
正方形的面积为$边长^2$，给定正方形的边长为4cm，所以正方形的面积为$4cm × 4cm = 16cm^2$。
由于阴影部分占据了正方形的一半，所以阴影部分的面积为$\frac{1}{2} × 16cm^2 = 8cm^2$。
【答案】：B. $8 cm^2$。

3. 如图,O 为正方形 ABCD 对角线 AC 的中点,△ACE 为等边三角形.若 AB= 2,则 OE 的长度为$\sqrt{6}$.

答案： 1. 首先，在正方形$ABCD$中：
已知$AB = 2$，根据勾股定理$a^{2}+b^{2}=c^{2}$（在正方形$ABCD$中，$AB = BC$，$AC$为对角线），可得$AC=\sqrt{AB^{2}+BC^{2}}$。
因为$AB = BC = 2$，所以$AC=\sqrt{2^{2}+2^{2}}=\sqrt{4 + 4}=\sqrt{8}=2\sqrt{2}$。
又因为$O$为$AC$中点，所以$AO=\frac{1}{2}AC$，则$AO=\frac{1}{2}×2\sqrt{2}=\sqrt{2}$。
2. 然后，在等边$\triangle ACE$中：
因为$\triangle ACE$是等边三角形，所以$AE = AC = 2\sqrt{2}$，$\angle EAC = 60^{\circ}$，且$EO\perp AC$（等边三角形三线合一，$O$是$AC$中点）。
3. 最后，在$Rt\triangle AOE$中：
根据勾股定理$OE=\sqrt{AE^{2}-AO^{2}}$。
把$AE = 2\sqrt{2}$，$AO=\sqrt{2}$代入可得：
$OE=\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}=\sqrt{8 - 2}=\sqrt{6}$。
故$OE$的长度为$\sqrt{6}$。

4. 如图,P 为 AB 上任意一点,分别以 AP,PB 为边在 AB 同侧作正方形 APCD、正方形 PBEF,设∠CBE= α,则∠AFP 的度数为____.

45°

答案： 解：
∵四边形PBEF是正方形，
∴PB=EF，∠PBE=90°，∠BEF=90°，
∵∠CBE=α，
∴∠PBC=∠PBE - ∠CBE=90° - α，
∵四边形APCD是正方形，
∴AP=PC，∠APC=90°，
设AP=PC=a，PB=EF=b，
在△APF和△CBP中，
AP=PC=a，∠PAF=∠CPB=90°，AF=PB=b，
∴△APF≌△CBP（SAS），
∴∠AFP=∠PBC=90° - α，
又
∵在正方形PBEF中，∠PFE=45°，
而∠AFP + ∠PFE=∠AFE，
但由正方形性质知∠AFE=45° + α，
故90° - α + 45°=45° + α，
解得α=45°，
∴∠AFP=90° - 45°=45°。
45°

5. 如图,正方形 ABCD 的边长为 8,点 E 是 CD 的中点,HG 垂直平分 AE 且分别交 AE,BC 于点 H,G,则 BG= ____1.

答案： 解：连接AG，EG。
∵四边形ABCD是正方形，边长为8，
∴AB=BC=CD=AD=8，∠B=∠C=90°。
∵E是CD中点，
∴DE=CE=4。
∵HG垂直平分AE，
∴AG=EG。
设BG=x，则GC=8-x。
在Rt△ABG中，AG²=AB²+BG²=8²+x²=64+x²。
在Rt△ECG中，EG²=CE²+GC²=4²+(8-x)²=16+(8-x)²。
∵AG=EG，
∴64+x²=16+(8-x)²。
展开得64+x²=16+64-16x+x²，
化简得0=16-16x，解得x=1。
∴BG=1。
1

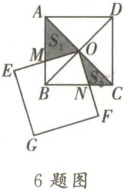
6. 如图,正方形 ABCD 的对角线相交于点 O,以点 O 为顶点的正方形 OEGF 的两边 OE,OF 分别交正方形 ABCD 的两边 AB,BC 于点 M,N,记△AOM 的面积为$ S_1,△CON $的面积为$ S_2,$若正方形的边长$ AB= 8,S_1= 10,$则$ S_2 $的大小为____.

6

答案： 解：
∵四边形ABCD是正方形，AB=8，
∴AC⊥BD，OA=OC=OB=OD，∠OAM=∠OCN=45°，AB=BC=8，
∴OA=OC= $\frac{1}{2}$AC= $\frac{1}{2}\sqrt{8^2+8^2}$=4$\sqrt{2}$。
设AM=x，
∵S₁=10，
∴S₁= $\frac{1}{2}$OA·AM·sin45°= $\frac{1}{2}×4\sqrt{2}× x×\frac{\sqrt{2}}{2}$=10，
解得x=5，即AM=5。
∵AB=8，
∴BM=AB-AM=3。
∵四边形OEGF是正方形，
∴∠EOF=90°，
又
∵∠AOB=90°，
∴∠AOM+∠MOB=∠BON+∠MOB=90°，
∴∠AOM=∠BON。
在△AOM和△BON中，
∠OAM=∠OBN=45°，OA=OB，∠AOM=∠BON，
∴△AOM≌△BON（ASA），
∴BN=AM=5。
∵BC=8，
∴CN=BC-BN=3。
则S₂= $\frac{1}{2}$OC·CN·sin45°= $\frac{1}{2}×4\sqrt{2}×3×\frac{\sqrt{2}}{2}$=6。
答案：6

7. 如图,正方形 ABCD 的对角线 AC 的长度为 3,E 为与点 D 不重合的动点,以 DE 为一边作正方形 DEFG.设$ DE= d_1,$点 F,G 与点 C 的距离分别为$ d_2,d_3.$
(1)求证:△ADE≌△CDG;
(2)求$ d_1 + d_2 + d_3 $的最小值.

答案：
(1)证明：
∵四边形ABCD和四边形DEFG都是正方形，
∴AD=CD，DE=DG，∠ADC=∠EDG=90°，
∴∠ADC - ∠EDC = ∠EDG - ∠EDC，即∠ADE=∠CDG，
在△ADE和△CDG中，
$\left\{\begin{array}{l}AD=CD\\ \angle ADE=\angle CDG\\ DE=DG\end{array}\right.$，
∴△ADE≌△CDG(SAS)；
(2)解：连接CF，AG，
由
(1)知△ADE≌△CDG，
∴AE=CG=d₃，
∵四边形DEFG是正方形，
∴DE=EF=d₁，∠DEF=90°，
∴点F在以DE为边的正方形的顶点处，且EF=d₁，
要使d₁ + d₂ + d₃ = DE + CF + CG = EF + CF + AE，
当点A，E，F，C四点共线时，AE + EF + CF最小，最小值为AC的长度，
∵AC=3，
∴d₁ + d₂ + d₃的最小值为3。
答案：
(2)3

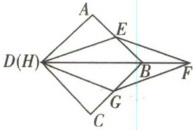
8. 将正方形 ABCD 和菱形 EFGH 按照如图所示摆放,顶点 D 与顶点 H 重合,菱形 EFGH 的对角线 HF 经过点 B,点 E,G 分别在 AB,BC 上.
(1)求证:△ADE≌△CDG;
(2)若 AE= BE= 2,求 BF 的长.

答案：
(1)证明：
∵四边形ABCD是正方形，
∴AD=CD，∠A=∠C=90°，∠ADC=90°，
∵四边形EFGH是菱形，
∴DE=DG，∠EDH=∠GDH，
∵∠ADC=∠EDH+∠GDH=90°，
∴∠ADE+∠EDC=∠CDG+∠EDC=90°，
∴∠ADE=∠CDG，
在△ADE和△CDG中，
$\left\{\begin{array}{l}AD=CD\\ \angle ADE=\angle CDG\\ DE=DG\end{array}\right.$，
∴△ADE≌△CDG(SAS)；
(2)解：
∵AE=BE=2，
∴AB=AE+BE=4，
∵四边形ABCD是正方形，
∴AD=AB=4，∠A=90°，
在Rt△ADE中，DE=$\sqrt{AD^2+AE^2}=\sqrt{4^2+2^2}=2\sqrt{5}$，
∵△ADE≌△CDG，
∴CG=AE=2，
∵BC=AB=4，
∴BG=BC-CG=4-2=2，
∵四边形EFGH是菱形，
∴EH=GH=DE=2$\sqrt{5}$，HF平分∠EHG，
∴∠EHB=∠GHB，
在△EHB和△GHB中，
$\left\{\begin{array}{l}EH=GH\\ \angle EHB=\angle GHB\\ HB=HB\end{array}\right.$，
∴△EHB≌△GHB(SAS)，
∴EB=GB=2，∠EBH=∠GBH，
∵∠ABC=90°，
∴∠EBH=∠GBH=45°，
过点E作EM⊥HF于M，过点B作BN⊥HF于N，
则EM=EB·sin45°=2×$\frac{\sqrt{2}}{2}=\sqrt{2}$，BN=EB·sin45°=$\sqrt{2}$，
EN=EB·cos45°=2×$\frac{\sqrt{2}}{2}=\sqrt{2}$，
∵∠EMH=90°，
在Rt△EMH中，HM=$\sqrt{EH^2-EM^2}=\sqrt{(2\sqrt{5})^2-(\sqrt{2})^2}=\sqrt{20-2}=\sqrt{18}=3\sqrt{2}$，
∴HN=HM-EN=3$\sqrt{2}-\sqrt{2}=2\sqrt{2}$，
∴BF=HF-HB，
∵HF=HM+MF，HB=HN+NB，
又
∵MF=NB=$\sqrt{2}$，
∴BF=HM+MF-(HN+NB)=3$\sqrt{2}+\sqrt{2}-(2\sqrt{2}+\sqrt{2})=4\sqrt{2}-3\sqrt{2}=\sqrt{2}$。
答：BF的长为$\sqrt{2}$。