《2025年本土假期作业巩固训练八年级数学》

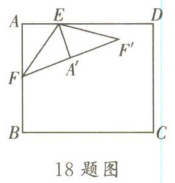
18. 如图,在矩形纸片ABCD中,AB= 4,AD= 5,点F是AB的中点,点E为AD上一动点,作△AEF关于直线EF的对称图形,点A的对应点为点A',作△A'EF关于直线A'E的对称图形,点F的对应点为F'。当点F'落在矩形ABCD的边上时,AE的长为______。

答案： 解：设AE=x。
情况一：点F'落在BC边上
过A'作A'M⊥AD于M，A'N⊥AB于N，设A'M=a，A'N=b。
由对称性质得：AE=A'E=x，AF=A'F=2，∠AEF=∠A'EF，∠FA'E=∠FAE=90°。
则有：b² + (2 - a)² = 2²，(5 - b)² + a² = x²，x² + 2² = (a + x)² + (b - 2)²（EF²相等）。
解得x=√5。
情况二：点F'落在CD边上
由对称性质得：A'E=AE=x，A'F=AF=2，EF'=EF=√(x² + 4)，∠FA'E=∠FAE=90°，∠A'EF=∠A'EF'。
则DF'=4 - 2=2，CF'=4 - DF'=2。
在Rt△EDF'中，(5 - x)² + 2² = (√(x² + 4) + √(x² + 4))²（EF'=2EF）。
解得x=5/3。
综上，AE的长为√5或5/3。
答案：√5或5/3

19. 如图,过△ABC的顶点A分别作∠ACB及其外角的平分线的垂线,垂足分别为E,F,求证：四边形AECF是矩形。

答案： 证明：
∵ CE平分∠ACB，CF平分∠ACD，
∴ ∠ACE=∠BCE=1/2∠ACB，∠ACF=∠DCF=1/2∠ACD。
∵ ∠ACB+∠ACD=180°，
∴ ∠ECF=∠ACE+∠ACF=1/2(∠ACB+∠ACD)=90°。
∵ AE⊥CE，AF⊥CF，
∴ ∠AEC=∠AFC=90°。
∴ 四边形AECF是矩形（三个角是直角的四边形是矩形）。

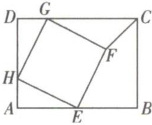
20. 如图,在矩形ABCD中,AD= 6,DC= 8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH= 2,DG= 2。求证：四边形EFGH为正方形。

答案： 证明：
∵ 四边形ABCD是矩形，
∴ ∠A=∠D=90°，AB=CD=8，AD=BC=6。
∵ AH=2，DG=2，
∴ HD=AD-AH=6-2=4，AE=AB-EB=8-EB（设EB=x，则AE=8-x）。
∵ 四边形EFGH是菱形，
∴ EH=HG，EH//FG，HG//EF。
在Rt△AEH中，EH²=AH²+AE²=2²+(8-x)²=4+(8-x)²。
在Rt△DHG中，HG²=HD²+DG²=4²+2²=16+4=20。
∵ EH=HG，
∴ 4+(8-x)²=20，
解得x=8-4=4（x=8+4舍去），
∴ AE=8-4=4，EB=4。
∴ EH²=20，EH=2√5；
AH=2，AE=4，HD=4，DG=2。
∵ ∠A=∠D=90°，
∴ tan∠AEH=AH/AE=2/4=1/2，tan∠DHG=DG/HD=2/4=1/2，
∴ ∠AEH=∠DHG。
∵ ∠AEH+∠AHE=90°，
∴ ∠DHG+∠AHE=90°，
∴ ∠EHG=180°-90°=90°。
∵ 四边形EFGH是菱形且有一个角为90°，
∴ 四边形EFGH为正方形。

21. 如图,△ABC中,AB= AC,AD,CD分别是△ABC两个外角的平分线。
(1)求证：AC= AD；
(2)若∠B= 60°,求证：四边形ABCD是菱形。

答案：
(1)证明：
∵AB=AC，
∴∠B=∠ACB，
∵AD平分∠FAC，
∴∠FAD=∠CAD=1/2∠FAC，
∵∠FAC=∠B+∠ACB=2∠B，
∴∠CAD=∠B，
∴AD//BC，
∴∠ADC=∠DCE，
∵CD平分∠ACE，
∴∠ACD=∠DCE，
∴∠ADC=∠ACD，
∴AC=AD；
(2)证明：
∵∠B=60°，AB=AC，
∴△ABC是等边三角形，
∴AB=BC=AC，∠ACB=60°，
∴∠FAC=∠ACE=120°，
∵AD平分∠FAC，CD平分∠ACE，
∴∠CAD=60°，∠ACD=60°，
∴△ACD是等边三角形，
∴AD=CD=AC，
∴AD=BC，AB=CD，
∴四边形ABCD是平行四边形，
∵AB=BC，
∴四边形ABCD是菱形。

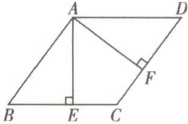
22. 如图,四边形ABCD是菱形,AE⊥BC于点E,AF⊥CD于点F。
(1)求证：△ABE≌△ADF；
(2)若AE= 4,CF= 2,求菱形的边长。

答案： 【解析】：
(1)本题可根据菱形的性质得到对应边相等和对应角相等，再结合垂直的性质，利用全等三角形的判定定理来证明$\triangle ABE\cong\triangle ADF$。
(2)在
(1)的基础上，根据全等三角形的性质得到对应边相等，设出菱形的边长，再利用勾股定理建立方程，进而求出菱形的边长。
【答案】：
(1)证明：
∵四边形$ABCD$是菱形，
∴$AB = AD$，$\angle B = \angle D$。
∵$AE\perp BC$，$AF\perp CD$，
∴$\angle AEB = \angle AFD = 90^{\circ}$。
在$\triangle ABE$和$\triangle ADF$中，
$\begin{cases}\angle B = \angle D\\\angle AEB = \angle AFD\\AB = AD\end{cases}$
∴$\triangle ABE\cong\triangle ADF(AAS)$。
(2)解：
设菱形的边长为$x$。
由
(1)知$\triangle ABE\cong\triangle ADF$，
∴$BE = DF$。
∵$BC = CD$，$CF = 2$，
∴$BE = DF = x - 2$。
在$Rt\triangle ABE$中，$AB = x$，$BE = x - 2$，$AE = 4$，
根据勾股定理$AB^{2}=AE^{2}+BE^{2}$，可得：
$x^{2}=4^{2}+(x - 2)^{2}$
$x^{2}=16 + x^{2}- 4x + 4$
$4x = 20$
解得$x = 5$。
∴菱形的边长为$5$。