《2025年本土假期作业巩固训练八年级数学》

1. 如图,平行四边形$ABCD的对角线AC$,$BD相交于点O$,若$AC= 4$,$BD= 6$,则$AB$的长可能是 (D)
A.7
B.6
C.5

D.4

答案： 【解析】：
首先，由平行四边形的性质，我们知道平行四边形的对角线互相平分。
所以，$AO = \frac{AC}{2} = \frac{4}{2} = 2$，$BO = \frac{BD}{2} = \frac{6}{2} = 3$。
接下来，我们考虑三角形$AOB$。
根据三角形的三边关系，任意两边之和大于第三边，任意两边之差小于第三边。
所以，在$\triangle AOB$中，有：
$AO + BO ＞ AB$，即 $2 + 3 ＞ AB$，得到 $AB ＜ 5$。
$AB ＞ |AO - BO|$，即 $AB ＞ |2 - 3| = 1$，但这个不等式对确定AB的范围帮助不大，因为AB显然会大于1。
更重要的是，我们需要考虑AO与BO之和与AB的关系来确定AB的上限，即 $AB ＜ 5$。
同时，由于平行四边形的对边相等，且对角线将平行四边形分为两个共轭的三角形，AB的长度应大于0且小于$AO$与$BO$之和，且由于题目中的选项都是整数，我们需要考虑最接近的整数值。
综合以上分析，我们可以得出AB的可能长度是小于5且大于0的整数，结合选项，只有4满足条件（注意，5是不满足的，因为当AB等于5时，A，O，B三点共线，不能构成三角形）。
但这里我们需要更精确地理解“可能”的含义，在几何中，当说到一条线段的“可能”长度时，它通常指的是满足所有几何条件的所有可能长度中的某一个。
由于AB必须小于5且大于1（由三角形不等式得出），并且题目中的选项是整数，结合平行四边形的性质，我们可以确定AB的可能最大整数值是小于5的最大整数，即4（因为5时A，O，B共线，不能构成三角形）。
而虽然1也是可能的，但在选择题的上下文中，我们通常寻找的是满足所有条件且最符合题意的答案，因此这里应选择4作为答案，因为它是小于5的最大整数且能使得A，O，B构成三角形。
【答案】：
D. $4$。

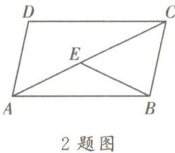
2. 在探索数学名题“尺规三等分角”的过程中,有下面的问题：如图,$AC是□ ABCD$的对角线,$AD= AE= BE$,$∠D= 108^{\circ}$,则$∠BAC= $ (A)

A.$24^{\circ}$
B.$36^{\circ}$
C.$60^{\circ}$
D.$45^{\circ}$

答案： 解：
∵四边形ABCD是平行四边形，∠D=108°，
∴∠ABC=∠D=108°，AD=BC，AB//CD，
∴∠BAD=180°-∠D=72°.
∵AD=AE=BE，
∴BC=AE=BE，
∴∠EAB=∠EBA，∠BEC=∠BCE.
设∠BAC=x，则∠EAB=∠EBA=72°-x，
∴∠BEC=∠EAB+∠EBA=144°-2x，
∠EBC=∠ABC-∠EBA=108°-(72°-x)=36°+x，
∴∠BCE=180°-∠EBC-∠BEC=180°-(36°+x)-(144°-2x)=x，
∴∠BCE=∠BAC=x，
∵AB//CD，
∴∠BAC=∠ACD=x，
∴∠ACB=∠BCE+∠ACD=2x，
在△ABC中，∠BAC+∠ABC+∠ACB=180°，
即x+108°+2x=180°，
解得x=24°，
∴∠BAC=24°.
答案：A.

3. 如下是小明对“平行四边形的对角线互相平分”的证明过程.
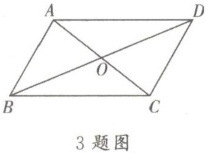
已知：如图,四边形$ABCD$是平行四边形,对角线$AC$,$BD交于点O$.
求证：$AO= OC$,$BO= OD$.
证明：$\because$ 四边形$ABCD$是平行四边形
$\therefore AD= BC$,____,
$\therefore ∠OAD= ∠OCB$,$∠ODA= ∠OBC$,
$\therefore \triangle OAD\cong\triangle OCB$,
$\therefore AO= OC$,$BO= OD$.
则在“____”处应该补充的证明过程是 (A)

A.$AD// BC$
B.$AB// CD$
C.$∠ABO= ∠CDO$

D.$AB= CD$

答案： 【解析】：
首先，我们回顾平行四边形的性质。
在平行四边形中，对边平行且相等。
题目中已给出四边形$ABCD$是平行四边形，且$AD=BC$。
接下来，我们需要找到一个与$AD=BC$相对应，且能推导出$\angle OAD = \angle OCB$和$\angle ODA = \angle OBC$的条件。
观察选项：
A. $AD // BC$：这是平行四边形的一个基本性质，且能由此推导出内错角相等，即$\angle OAD = \angle OCB$和$\angle ODA = \angle OBC$。
B. $AB // CD$：虽然这也是平行四边形的一个性质，但它不能直接推导出题目中所需的角度相等关系。
C. $\angle ABO = \angle CDO$：这个条件并不能直接由平行四边形的性质得出，且不能推导出题目中所需的角度相等关系。
D. $AB = CD$：这是平行四边形对边相等的一个性质，但与推导出题目中所需的角度相等关系无直接帮助。
因此，在“____”处应该补充的证明过程是$AD // BC$，因为这是能推导出$\angle OAD = \angle OCB$和$\angle ODA = \angle OBC$的关键条件。
【答案】：A

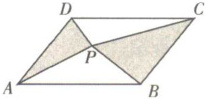
4. 如图,$P是面积为S的平行四边形ABCD$内任意一点,$\triangle PAD的面积为S_{1}$,$\triangle PBC的面积为S_{2}$,则 (C)

A.$S_{1}+S_{2}＞\frac{S}{2}$
B.$S_{1}+S_{2}＜\frac{S}{2}$
C.$S_{1}+S_{2}= \frac{S}{2}$
D.$S_{1}+S_{2}的大小与P$点位置有关

答案： 【解析】：本题可根据平行四边形的性质以及三角形面积公式来求解$S_1 + S_2$与$\frac{S}{2}$的关系。
设平行四边形$ABCD$的底边$AB = CD = a$，$AB$边上的高为$h$，根据平行四边形面积公式$S = 底×高$，可得$S = ah$。
过点$P$作$PE\perp AD$于点$E$，$PF\perp BC$于点$F$，因为$AD// BC$，且平行线间的距离处处相等，所以$PE + PF = h$。
根据三角形面积公式$S=\frac{1}{2}×底×高$，可得$S_1=\frac{1}{2}AD× PE$，$S_2=\frac{1}{2}BC× PF$。
由于$AD = BC = a$，则$S_1 + S_2=\frac{1}{2}AD× PE+\frac{1}{2}BC× PF=\frac{1}{2}a× PE+\frac{1}{2}a× PF=\frac{1}{2}a(PE + PF)$。
把$PE + PF = h$代入上式，可得$S_1 + S_2=\frac{1}{2}ah$，又因为$S = ah$，所以$S_1 + S_2=\frac{S}{2}$，即$S_1 + S_2$的大小与$P$点位置无关。
【答案】：C

5. 如图,平行四边形$ABCD$中,$DE平分∠ADC$,交$BC于点E$,$∠DEC= 28^{\circ}$,则$∠B$的度数是____$^{\circ}$.


56

答案： 解：
∵四边形$ABCD$是平行四边形，
∴$AD// BC$，$∠B=∠ADC$（平行四边形对边平行，对角相等）。
∵$AD// BC$，
∴$∠ADE=∠DEC=28^{\circ}$（两直线平行，内错角相等）。
∵$DE$平分$∠ADC$，
∴$∠ADC=2∠ADE=2×28^{\circ}=56^{\circ}$。
∴$∠B=∠ADC=56^{\circ}$。
$56$

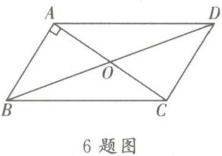
6. 如图,四边形$ABCD$是平行四边形,$O是对角线AC与BD$的交点,$AB⊥AC$,若$AB= 8$,$AC= 12$,则$BD$的长是____.

20

答案： 【解析】：
由题意可知，四边形$ABCD$是平行四边形，根据平行四边形的性质对角线互相平分，
我们可以得出$OA=\frac{1}{2}AC$，$OB=\frac{1}{2}BD$，
题目给出$AB⊥AC$，$AB=8$，$AC=12$，
我们可以利用勾股定理在直角三角形$ABO$中求$BO$的长度，
$OA=\frac{1}{2}AC=6$，
根据勾股定理，我们有$BO=\sqrt{AB^{2}+OA^{2}}=\sqrt{8^{2}+6^{2}}=10$，
因为$OB=\frac{1}{2}BD$，
我们可以得出$BD=2BO=20$，
所以$BD$的长度是20。
【答案】：
20。

7. 如图,在平行四边形$ABCD$中,$AD= a$,$AB= b$,$(a＞b)AE平分∠BAD$,交边$BC于点E$,$DF平分∠ADC$,交边$BC于点F$,则$EF= $2b-a.

答案： 解：
∵四边形ABCD是平行四边形，
∴AD//BC，AB=CD=b，AD=BC=a，
∴∠DAE=∠AEB，∠ADF=∠DFC，
∵AE平分∠BAD，DF平分∠ADC，
∴∠DAE=∠BAE，∠ADF=∠CDF，
∴∠AEB=∠BAE，∠DFC=∠CDF，
∴BE=AB=b，CF=CD=b，
∵BC=BE+EF+FC，
∴a=b+EF+b，
∴EF=2b-a。
答案：2b-a

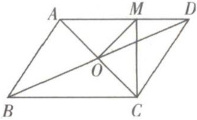
8. 如图,$□ ABCD的对角线相交于点O$,且$AD≠CD$,过点$O作OM⊥AC$,交$AD于点M$.
(1) 若$\triangle CDM$的周长为 8,求$□ ABCD$的周长；
(2) 若$∠ADC= 78^{\circ}$,$CM平分∠ACD$,试求$∠BCA$的度数.

答案：
(1)解：
∵四边形ABCD是平行四边形，
∴OA=OC，AB=CD，AD=BC。
∵OM⊥AC，
∴AM=CM（线段垂直平分线上的点到线段两端距离相等）。
∵△CDM的周长=CD+DM+CM=8，
又
∵CM=AM，
∴CD+DM+AM=CD+AD=8。
∴□ABCD的周长=2(CD+AD)=2×8=16。
(2)解：设∠BCA=x。
∵四边形ABCD是平行四边形，
∴AD//BC，
∴∠DAC=∠BCA=x（两直线平行，内错角相等）。
∵AM=CM，
∴∠ACM=∠DAC=x。
∵CM平分∠ACD，
∴∠DCM=∠ACM=x，
∴∠ACD=2x。
∵AD//BC，
∴∠ADC+∠BCD=180°（两直线平行，同旁内角互补）。
∵∠ADC=78°，∠BCD=∠BCA+∠ACD=x+2x=3x，
∴78°+3x=180°，
解得x=34°，即∠BCA=34°。