《2025年本土假期作业巩固训练八年级数学》

专题 1 矩形的性质
知识清单
1. 定义:有一个角是直角的平行四边形叫做矩形.
2. 矩形的性质
(1)矩形的对边平行且相等;
(2)矩形的四个角都是直角;
(3)矩形的对角线相等且互相平分;
(4)矩形既是轴对称图形又是中心对称图形.
3. 直角三角形斜边上的中线长度等于斜边的一半.

答案： 1. 直角
2.
(1)平行且相等
(2)都是直角
(3)相等且互相平分
3. 斜边的一半

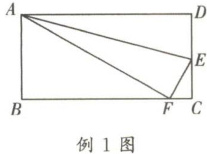
例 1 如图,分别在长方形 ABCD 的边 DC,BC 上取两点 E,F,使得 AE 平分∠DAF,若∠BAF= 60°,则∠DAE= (  )

A.45°
B.30°
C.15°
D.60°

答案： 【解析】：
本题主要考查长方形中的角度计算以及角平分线的性质。
首先，长方形$ABCD$的内角都是$90^\circ$。
已知$\angle BAF = 60^\circ$，
根据长方形内角为$90^\circ$的性质，我们可以计算出$\angle DAF$的度数：
$\angle DAF = 90^\circ - \angle BAF = 90^\circ - 60^\circ = 30^\circ$，
接下来，根据题目条件，$AE$平分$\angle DAF$，
根据角平分线的定义，$\angle DAE$是$\angle DAF$的一半，
即：$\angle DAE = \frac{1}{2} \angle DAF = \frac{1}{2} × 30^\circ = 15^\circ$。
【答案】：C.$15^\circ$。

例 2 如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O,已知∠ACB= 25°,则∠AOB 的大小是 (  )


A.130°
B.65°
C.50°
D.25°

答案： 解：
∵四边形ABCD是矩形，
∴AC=BD，OA=OC=1/2AC，OB=OD=1/2BD，
∴OB=OC，
∴∠OBC=∠ACB=25°，
∵∠AOB是△OBC的外角，
∴∠AOB=∠OBC+∠ACB=25°+25°=50°．
故选：C．

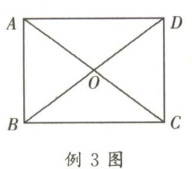
例 3 如图,矩形 ABCD 的周长为 28 cm,对角线 AC,BD 将矩形分成四个小三角形,若四个小三角形的周长和为 68 cm,AC 的长度为 (  )

A.10 cm
B.14 cm
C.16 cm
D.无法确定

答案： 解：
∵四边形ABCD是矩形，
∴AC=BD，OA=OC=OB=OD，AB=CD，AD=BC。
∵矩形ABCD的周长为28cm，
∴2AB+2BC=28cm。
∵四个小三角形（△AOB、△BOC、△COD、△DOA）的周长和为68cm，
∴(OA+OB+AB)+(OB+OC+BC)+(OC+OD+CD)+(OD+OA+AD)=68cm。
∵AB=CD，AD=BC，OA=OB=OC=OD，
∴4×2OA + 2AB + 2BC=68cm，即8OA + 28=68cm。
解得OA=5cm。
∵AC=2OA，
∴AC=10cm。
答案：A

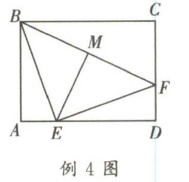
例 4 如图,两点 E,F 分别在矩形 ABCD 的 AD 和 CD 边上,AB= 6,AD= 8,∠BEF= 90°,且 BE= EF,点 M 为 BF 的中点,则 ME 的长为____.

答案： 解：
∵四边形ABCD是矩形，
∴∠A=∠D=90°，AB=CD=6，AD=BC=8，
∴∠ABE+∠AEB=90°，
∵∠BEF=90°，
∴∠AEB+∠DEF=90°，
∴∠ABE=∠DEF，
在△ABE和△DEF中，
$\left\{\begin{array}{l} ∠A=∠D\\ ∠ABE=∠DEF\\ BE=EF\end{array}\right. $，
∴△ABE≌△DEF（AAS），
∴AE=DF，AB=DE=6，
∵AD=8，
∴AE=AD-DE=8-6=2，
∴DF=AE=2，
∴CF=CD-DF=6-2=4，
在Rt△BCF中，BC=8，CF=4，
∴BF=$\sqrt{B{C}^{2}+C{F}^{2}}=\sqrt{{8}^{2}+{4}^{2}}=\sqrt{80}=4\sqrt{5}$，
∵∠BEF=90°，点M为BF的中点，
∴ME=$\frac{1}{2}$BF=$\frac{1}{2}×4\sqrt{5}=2\sqrt{5}$．
故答案为：$2\sqrt{5}$．

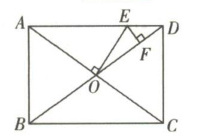
例 5 如图,矩形 ABCD 的对角线 AC,BD 交于点 O,AB= 6,BC= 8,过点 O 作 OE⊥AC,交 AD 于点 E,过点 E 作 EF⊥BD,垂足为点 F,则 OE+EF 的值为____.

答案： 【解析】：本题可根据矩形的性质求出$\triangle AOD$的面积，再结合三角形面积公式，通过$S_{\triangle AOD}= S_{\triangle AOE}+S_{\triangle DOE}$来求解$OE + EF$的值。
步骤一：求出矩形$ABCD$的面积和对角线$AC$、$BD$的长度
已知在矩形$ABCD$中，$AB = 6$，$BC = 8$，根据矩形面积公式$S = 长×宽$，可得矩形$ABCD$的面积为$AB× BC = 6× 8 = 48$。
因为矩形的对角线相等且互相平分，所以$AC = BD$，且$AC$、$BD$互相平分于点$O$，即$AO = OC=\frac{1}{2}AC$，$BO = OD=\frac{1}{2}BD$，那么$AO = DO$。
根据勾股定理$a^2+b^2=c^2$（其中$a$、$b$为直角边，$c$为斜边），可得$AC = \sqrt{AB^{2} + BC^{2}} = \sqrt{6^{2} + 8^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10$，所以$AO = DO = \frac{1}{2}AC = 5$。
步骤二：求出$\triangle AOD$的面积
由于矩形的对角线将矩形分成面积相等的四个三角形，所以$\triangle AOD$的面积为矩形$ABCD$面积的$\frac{1}{4}$，即$S_{\triangle AOD}=\frac{1}{4}×48 = 12$。
步骤三：根据三角形面积公式表示出$S_{\triangle AOE}$和$S_{\triangle DOE}$
因为$OE\perp AC$，$EF\perp BD$，根据三角形面积公式$S = \frac{1}{2}×底×高$，可得$S_{\triangle AOE}=\frac{1}{2}AO\cdot OE$，$S_{\triangle DOE}=\frac{1}{2}DO\cdot EF$。
步骤四：根据$S_{\triangle AOD}= S_{\triangle AOE}+S_{\triangle DOE}$求出$OE + EF$的值
将$S_{\triangle AOE}=\frac{1}{2}AO\cdot OE$，$S_{\triangle DOE}=\frac{1}{2}DO\cdot EF$代入$S_{\triangle AOD}= S_{\triangle AOE}+S_{\triangle DOE}$，可得$S_{\triangle AOD}=\frac{1}{2}AO\cdot OE + \frac{1}{2}DO\cdot EF$。
又因为$AO = DO = 5$，$S_{\triangle AOD}= 12$，所以$12 = \frac{1}{2}× 5× OE + \frac{1}{2}× 5× EF$，即$12 = \frac{5}{2}(OE + EF)$。
等式两边同时乘以$\frac{2}{5}$，可得$OE + EF = 12×\frac{2}{5}=\frac{24}{5}= 4.8$。
【答案】：$4.8$

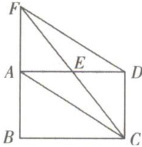
例 6 如图,在矩形 ABCD 中,E 是 AD 的中点,延长 CE,BA 交于点 F,连结 AC,DF.
(1)求证:四边形 ACDF 是平行四边形;
(2)当 CF 平分∠BCD 时,写出 BC 与 CD 的数量关系,并说明理由.

答案：
(1)证明：
∵四边形ABCD是矩形，
∴AB//CD，
∴∠FAE=∠CDE，
∵E是AD的中点，
∴AE=DE，
又
∵∠FEA=∠CED，
∴△FAE≌△CDE(ASA)，
∴CD=FA，
又
∵CD//FA，
∴四边形ACDF是平行四边形；
(2)BC=2CD，理由：
∵CF平分∠BCD，
∴∠DCE=45°，
∵∠CDE=90°，
∴△CDE是等腰直角三角形，
∴CD=DE，
∵E是AD的中点，
∴AD=2DE=2CD，
∵AD=BC，
∴BC=2CD。