《2025年本土假期作业巩固训练八年级数学》

10. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE= CF,连结EF,EF与对角线AC交于点O,且BE= BF,∠BEF= 2∠BAC,FC= √3,则AB的长为(B)
A.2√3
B.3√3
C.4√3
D.6

答案： 解：
∵四边形ABCD是矩形，
∴AB=CD，AB//CD，∠ABC=90°，
∴∠OAE=∠OCF，∠OEA=∠OFC，
∵AE=CF，
∴△AOE≌△COF（AAS），
∴OA=OC，OE=OF，即O为AC、EF中点．
设∠BAC=α，则∠BEF=2α，
∵BE=BF，BO=BO，OE=OF，
∴△BOE≌△BOF（SSS），
∴∠OBE=∠OBF，∠BOE=∠BOF=90°，即BO⊥EF．
在Rt△BOE中，∠BEF=2α，∠BOE=90°，
∴∠OBE=90°-2α，
∵O为AC中点，矩形ABCD中BO=AO=OC，
∴∠OBA=∠BAC=α，
∵∠ABC=∠OBA+∠OBE+∠OBF=90°，∠OBE=∠OBF，
∴α+2(90°-2α)=90°，解得α=30°，即∠BAC=30°．
∵FC=√3，AE=CF=√3，设AB=x，则BE=x-√3，
在Rt△ABC中，∠BAC=30°，BC=AB·tan30°=√3/3 x，
∵AB//CD，
∴∠OFC=∠OEA=∠BEF=2α=60°，
在Rt△BCF中，BF=BE=x-√3，FC=√3，BC=√3/3 x，
由勾股定理：BF²=BC²+FC²，
即(x-√3)²=(√3/3 x)²+(√3)²，
解得x=3√3（x=0舍去），
∴AB=3√3．
答案：B.3√3

11. 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A'处,连结A'C,则∠BA'C= ______。

67.5°

答案： 解：
∵四边形ABCD是正方形，
∴AB=BC，∠CBD=45°，∠BCD=90°。
由折叠性质得：A'B=AB，
∴A'B=BC。
∴△BA'C是等腰三角形，∠BA'C=∠BCA'。
在△BA'C中，∠A'BC=45°，
∠BA'C+∠BCA'+∠A'BC=180°，
∴2∠BA'C+45°=180°，
解得∠BA'C=67.5°。
67.5°

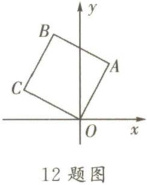
12. 已知正方形OABC在直角坐标系中(如图),若点A的坐标为(1,3),则点C的坐标为(-3,1)。

答案： 解：设点O坐标为$(x,y)$，点C坐标为$(m,n)$。
因为OABC是正方形，所以$\overrightarrow{OA}=(1-x,3-y)$，$\overrightarrow{OC}=(m-x,n-y)$，且$|\overrightarrow{OA}|=|\overrightarrow{OC}|$，$\overrightarrow{OA}\cdot\overrightarrow{OC}=0$。
又因为$\overrightarrow{AB}=\overrightarrow{OC}$，点B坐标为$(m,n)+(1-x,3-y)=(m+1-x,n+3-y)$，同时点B也可表示为$(1,3)+\overrightarrow{BC}$，而$\overrightarrow{BC}=-\overrightarrow{OA}$，所以点B坐标为$(1-(1-x),3-(3-y))=(x,y)$，即点B与点O重合，矛盾。
重新考虑，正方形OABC中，OA与OC垂直且相等，向量$\overrightarrow{OA}=(1,3)$，则向量$\overrightarrow{OC}$可能为$(-3,1)$或$(3,-1)$（因为两垂直向量数量积为0且模长相等）。
当$\overrightarrow{OC}=(-3,1)$时，点C坐标为$(-3,1)$；当$\overrightarrow{OC}=(3,-1)$时，点C坐标为$(3,-1)$。
由于正方形顶点顺序，结合坐标系，点C坐标为$(-3,1)$。
$(-3,1)$

13. 如图,矩形纸片ABCD中,AB= 6cm,BC= 8cm,现将其沿EF对折,使得点C与点A重合,则AF的长为6.25cm。

答案： 解：设AF=x cm，
∵矩形ABCD中，AD=BC=8cm，
∴DF=AD-AF=(8-x)cm。
∵沿EF对折后点C与点A重合，
∴AF=CF=x cm。
在Rt△CDF中，CD=AB=6cm，
由勾股定理得：CF²=CD²+DF²，
即x²=6²+(8-x)²，
x²=36+64-16x+x²，
16x=100，
x=6.25。
故AF的长为6.25 cm。

14. 如图,菱形ABCD的对角线的长分别为2和6,P是对角线AC上任一点(点P不与点A,C重合),且PE//BC,交AB于点E,PF//CD,交AD于点F,则阴影部分的面积是______。

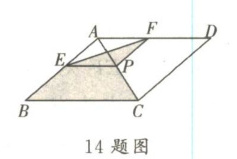
3

答案： 解：
∵菱形ABCD对角线长分别为2和6，
∴菱形面积$S=\frac{1}{2}×2×6=6$。
∵PE//BC，PF//CD，
∴四边形AEPF为平行四边形，
∴阴影部分面积等于$\triangle ABC$面积。
∵菱形对角线互相平分，
∴$\triangle ABC$面积为菱形面积的一半，即$\frac{1}{2}×6=3$。
故阴影部分面积是3。
答案：3

15. 如图,四边形ABCD中,∠ABC= ∠D= 120°,AB= BC= CD= DA,E是边AD上的一点,且∠ABE= 48°,若线段BE上存在点P,使∠CPB= ∠CPD,则∠ADP的度数为______。

30°

答案： 解：
∵AB=BC=CD=DA，
∴四边形ABCD为菱形。
∵∠ABC=120°，
∴∠BAD=60°，△ABD为等边三角形，∠ADB=60°。
∵∠ABE=48°，∠ABD=60°，
∴∠EBD=∠ABD-∠ABE=12°。
∵线段BE上存在点P使∠CPB=∠CPD，
∴CP平分∠BPD，结合BC=CD，易证△CPB≌△CPD（SAS），
∴PB=PD，即P在BD的垂直平分线上。
又
∵菱形ABCD中，AC垂直平分BD，
∴点P为BE与AC的交点。
连接AC交BD于O，易证△ABO≌△ADO（SSS），∠BAO=30°。
在△ABE中，∠AEB=180°-∠BAE-∠ABE=72°。
在△AEP中，∠EAP=∠BAO=30°，∠APE=78°。
∵∠DPO=∠BPO=∠EBD+∠BEP=12°+（180°-72°）=120°，
∴∠PDO=30°，∠ADP=∠ADB-∠PDO=60°-30°=30°。
答案：30°

16. 如图,菱形ABCD的边长为2,∠ABC= 60°,E是AD边的中点,点P是对角线BD上的动点,则AP+PE的最小值是______。

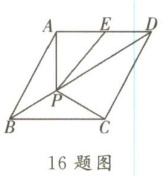
√3

答案： 解：连接AC，CE，CE与BD交于点P。
∵菱形ABCD，
∴点A与点C关于BD对称，
∴AP=CP。
∴AP+PE=CP+PE=CE。
∵菱形边长为2，∠ABC=60°，
∴△ABC为等边三角形，AC=AB=2。
∵E是AD中点，AD=2，
∴AE=1。
∵AD//BC，∠ABC=60°，
∴∠BAD=120°。
在△ACE中，AC=2，AE=1，∠CAE=60°（∠CAD=60°）。
由余弦定理得：CE²=AC²+AE²-2·AC·AE·cos60°=2²+1²-2×2×1×(1/2)=4+1-2=3，
∴CE=√3。
即AP+PE的最小值是√3。
答案：√3

17. 如图,以△ABC的三边为边在BC上方分别作等边△ACD,△ABE,△BCF。且点A在△BCF内部。给出以下结论：①四边形ADFE是平行四边形；②当∠BAC= 150°时,四边形ADFE是矩形；③当AB= AC时,四边形ADFE是菱形；④当AB= AC,且∠BAC= 150°时,四边形ADFE是正方形。其中正确的结论有①②③(填上所有正确结论的序号)。

答案： 【解析】：本题主要考查了平行四边形、矩形、菱形、正方形的判定定理以及等边三角形的性质。
①因为$\triangle ABE$和$\triangle BCF$是等边三角形，所以$BE = AB$，$BF = BC$，$\angle EBA = \angle FBC = 60^\circ$。
则$\angle EBF = \angle ABC$（因为$\angle EBF = \angle EBA + \angle ABF - \angle FBC=\angle ABC+60^\circ-60^\circ=\angle ABC$）。
根据$SAS$判定定理，$\triangle EBF \cong \triangle ABC$，所以$EF = AC$。
又因为$\triangle ACD$是等边三角形，所以$AD = AC$，从而$EF = AD$。
同理，可以证明$\triangle DFC \cong \triangle ABC$，所以$DF = AB$，而$AB=AE$，所以$DF = AE$。
两组对边分别相等的四边形是平行四边形，所以四边形$ADFE$是平行四边形，故①正确。
②当$\angle BAC = 150^\circ$时，因为$\triangle ABE$和$\triangle ACD$是等边三角形，所以$\angle BAE = \angle CAD = 60^\circ$。
则$\angle EAD = 360^\circ - \angle BAE - \angle BAC - \angle CAD = 360^\circ - 60^\circ - 150^\circ - 60^\circ = 90^\circ$。
有一个角是直角的平行四边形是矩形，因为四边形$ADFE$是平行四边形，且$\angle EAD = 90^\circ$，所以四边形$ADFE$是矩形，故②正确。
③当$AB = AC$时，$AE = AB = AC = AD$，因为四边形$ADFE$是平行四边形，邻边相等的平行四边形是菱形，所以四边形$ADFE$是菱形，故③正确。
④当$AB = AC$且$\angle BAC = 150^\circ$时，虽然四边形$ADFE$是平行四边形且是菱形（由③知），但$\angle EAD = 90^\circ$（由②知）只能说明它是矩形，并不能同时满足菱形和矩形的所有条件成为正方形（正方形需要所有边相等且所有角都是直角，这里只是对角相等且有一个直角），故④错误。
【答案】：①②③