2025年本土假期作业巩固训练八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年本土假期作业巩固训练八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
1. 如图,已知四边形 ABCD 的对角线 AC,BD 相交于点 O,则下列能判断它是正方形的条件是 (
A.AB= BC= CD= DA
B.AO= BO= CO= DO,AC⊥BD
C.AO= CO,BO= DO,AC⊥BD
D.AB= BC,CD⊥DA
B
)A.AB= BC= CD= DA
B.AO= BO= CO= DO,AC⊥BD
C.AO= CO,BO= DO,AC⊥BD
D.AB= BC,CD⊥DA
答案:
【解析】:
本题考查正方形判定条件。
A选项:$AB=BC=CD=DA$,只能判定四边形是菱形,不能判定是正方形,因为正方形除了四边相等,还需要四个角都是直角,故A选项错误。
B选项:$AO=BO=CO=DO$,说明四边形的对角线相等且互相平分,根据对角线相等且互相平分的四边形是矩形;又因为$AC\perp BD$,即对角线互相垂直,而有一个角是直角的矩形是正方形,所以该四边形是正方形,故B选项正确。
C选项:$AO=CO$,$BO=DO$,只能判定四边形是平行四边形,$AC\perp BD$只能进一步判定该平行四边形是菱形,不能判定是正方形,故C选项错误。
D选项:$AB=BC$,$CD\perp DA$,只能说明有一组邻边相等且有一个角是直角,不能判定四边形是正方形,故D选项错误。
【答案】:B
本题考查正方形判定条件。
A选项:$AB=BC=CD=DA$,只能判定四边形是菱形,不能判定是正方形,因为正方形除了四边相等,还需要四个角都是直角,故A选项错误。
B选项:$AO=BO=CO=DO$,说明四边形的对角线相等且互相平分,根据对角线相等且互相平分的四边形是矩形;又因为$AC\perp BD$,即对角线互相垂直,而有一个角是直角的矩形是正方形,所以该四边形是正方形,故B选项正确。
C选项:$AO=CO$,$BO=DO$,只能判定四边形是平行四边形,$AC\perp BD$只能进一步判定该平行四边形是菱形,不能判定是正方形,故C选项错误。
D选项:$AB=BC$,$CD\perp DA$,只能说明有一组邻边相等且有一个角是直角,不能判定四边形是正方形,故D选项错误。
【答案】:B
2. 如图,在菱形 ABCD 中,对角线 AC,BD 相交于点 O,添加下列条件,能使菱形 ABCD 成为正方形的是 (
A.AC= BD
B.AC⊥BD
C.AD= AB
D.AC 平分∠DAB
A
)A.AC= BD
B.AC⊥BD
C.AD= AB
D.AC 平分∠DAB
答案:
解:菱形的性质:四条边相等,对角线互相垂直平分。
正方形是特殊的菱形,除具有菱形的性质外,还具有对角线相等的性质。
选项A:AC=BD,即对角线相等的菱形是正方形,符合题意。
选项B:菱形的对角线本身就互相垂直,AC⊥BD不能使菱形成为正方形。
选项C:菱形的四条边都相等,AD=AB是菱形本身具有的性质。
选项D:菱形的对角线平分一组对角,AC平分∠DAB是菱形本身具有的性质。
结论:能使菱形ABCD成为正方形的条件是A。
答案:A
正方形是特殊的菱形,除具有菱形的性质外,还具有对角线相等的性质。
选项A:AC=BD,即对角线相等的菱形是正方形,符合题意。
选项B:菱形的对角线本身就互相垂直,AC⊥BD不能使菱形成为正方形。
选项C:菱形的四条边都相等,AD=AB是菱形本身具有的性质。
选项D:菱形的对角线平分一组对角,AC平分∠DAB是菱形本身具有的性质。
结论:能使菱形ABCD成为正方形的条件是A。
答案:A
3. 如图,在矩形 ABCD 中,对角线 AC 与 BD 相交于点 O,添加下列条件不能判定矩形 ABCD 是正方形的是 (
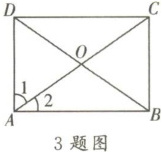
A.AB= BC
B.AC= BD
C.AC⊥BD
D.∠1= ∠2
B
)
A.AB= BC
B.AC= BD
C.AC⊥BD
D.∠1= ∠2
答案:
【解析】:
本题考查正方形的判定定理,需要对每个选项进行逐一的分析和判断。
A项:根据“有一组邻边相等的矩形是正方形”这一判定定理,当$AB=BC$时,矩形$ABCD$是正方形,故A项不符合题意。
B项:矩形的对角线本身就是相等的,即使$AC=BD$,也不能说明矩形$ABCD$是正方形,故B项符合题意。
C项:根据“对角线互相垂直的矩形是正方形”这一判定定理,当$AC\perp BD$时,矩形$ABCD$是正方形,故C项不符合题意。
D项:当$\angle 1=\angle 2$时,可以得出$AD// BC$,$AB=AD$。
根据“有一组邻边相等的矩形是正方形”这一判定定理,矩形$ABCD$是正方形,故D项不符合题意。
综上所述,答案为:B。
【答案】:B
本题考查正方形的判定定理,需要对每个选项进行逐一的分析和判断。
A项:根据“有一组邻边相等的矩形是正方形”这一判定定理,当$AB=BC$时,矩形$ABCD$是正方形,故A项不符合题意。
B项:矩形的对角线本身就是相等的,即使$AC=BD$,也不能说明矩形$ABCD$是正方形,故B项符合题意。
C项:根据“对角线互相垂直的矩形是正方形”这一判定定理,当$AC\perp BD$时,矩形$ABCD$是正方形,故C项不符合题意。
D项:当$\angle 1=\angle 2$时,可以得出$AD// BC$,$AB=AD$。
根据“有一组邻边相等的矩形是正方形”这一判定定理,矩形$ABCD$是正方形,故D项不符合题意。
综上所述,答案为:B。
【答案】:B
4. 如图,E,F,M,N 分别是正方形 ABCD 四条边上的点,AE= BF= CM= DN,则四边形 EFMN 的形状是 (
A.平行四边形
B.矩形
C.菱形
D.正方形
D
)A.平行四边形
B.矩形
C.菱形
D.正方形
答案:
证明:
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
∵AE=BF=CM=DN,设其长度为k,正方形边长为a,
则BE=CF=DM=AN=a-k。
在△AEN、△BFE、△CMF、△DNM中:
∵AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM(SAS)。
∴EN=FE=MF=NM,
∴四边形EFMN是菱形。
∵△AEN≌△BFE,
∴∠ANE=∠BEF。
∵∠A=90°,
∴∠ANE+∠AEN=90°,
∴∠BEF+∠AEN=90°,
∴∠NEF=180°-90°=90°。
∵四边形EFMN是菱形且有一个角为90°,
∴四边形EFMN是正方形。
答案:D
∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°。
∵AE=BF=CM=DN,设其长度为k,正方形边长为a,
则BE=CF=DM=AN=a-k。
在△AEN、△BFE、△CMF、△DNM中:
∵AE=BF=CM=DN,∠A=∠B=∠C=∠D,AN=BE=CF=DM,
∴△AEN≌△BFE≌△CMF≌△DNM(SAS)。
∴EN=FE=MF=NM,
∴四边形EFMN是菱形。
∵△AEN≌△BFE,
∴∠ANE=∠BEF。
∵∠A=90°,
∴∠ANE+∠AEN=90°,
∴∠BEF+∠AEN=90°,
∴∠NEF=180°-90°=90°。
∵四边形EFMN是菱形且有一个角为90°,
∴四边形EFMN是正方形。
答案:D
5. 现有一张边长等于 a(a>16)的正方形纸片,从距离正方形的四个顶点 8 cm 处,沿 45°角画线,将正方形纸片分成 5 部分,则阴影部分是
正方形
(填写图形的形状)(如图),它的一边长是8√2 cm
.
答案:
解:正方形;$8\sqrt{2}$cm
6. 如图,在四边形 ABCD 中,∠A= ∠B= 90°,AB= BC= 4,AD= 3,E 是边 AB 上一点,且∠DCE= 45°,则 DE 的长度是____
29/7
.
答案:
29/7
7. 如图,已知四边形 ABCD 为正方形,AB= √2,点 E 为对角线 AC 上一动点,连结 DE,过点 E 作 EF⊥DE,与 BC 相交于点 F,以 DE,EF 为邻边作矩形 DEFG,连结 CG.
(1)求证:矩形 DEFG 是正方形;
(2)探究:四边形 CEDG 的面积是否为定值? 若是,请求出这个定值;若不是,请说明理由.

(1)求证:矩形 DEFG 是正方形;
(2)探究:四边形 CEDG 的面积是否为定值? 若是,请求出这个定值;若不是,请说明理由.

答案:
(1)证明:过点E作EM⊥AD于M,EN⊥BC于N,EP⊥CD于P。
∵四边形ABCD是正方形,AC是对角线,
∴EM=EP,∠DME=∠EPF=90°,∠ACD=45°,
∴EP=PC,同理EM=MD。
∵EF⊥DE,
∴∠DEM+∠MEF=∠FEP+∠MEF=90°,
∴∠DEM=∠FEP。
在△DME和△EPF中,
∠DME=∠EPF,EM=EP,∠DEM=∠FEP,
∴△DME≌△EPF(ASA),
∴DE=EF。
∵四边形DEFG是矩形,
∴矩形DEFG是正方形。
(2)解:四边形CEDG的面积是定值,定值为1。
∵四边形DEFG是正方形,
∴DE=DG,∠EDG=90°。
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE+∠EDC=∠CDG+∠EDC=90°,
∴∠ADE=∠CDG。
在△ADE和△CDG中,
AD=CD,∠ADE=∠CDG,DE=DG,
∴△ADE≌△CDG(SAS),
∴S△ADE=S△CDG。
∵S四边形CEDG=S△CDE+S△CDG=S△CDE+S△ADE=S△ADC,
∵AB=√2,正方形ABCD中,AC=√2AB=2,AD=CD=√2,
S△ADC=1/2×AD×CD=1/2×√2×√2=1,
∴四边形CEDG的面积为1。
(1)证明:过点E作EM⊥AD于M,EN⊥BC于N,EP⊥CD于P。
∵四边形ABCD是正方形,AC是对角线,
∴EM=EP,∠DME=∠EPF=90°,∠ACD=45°,
∴EP=PC,同理EM=MD。
∵EF⊥DE,
∴∠DEM+∠MEF=∠FEP+∠MEF=90°,
∴∠DEM=∠FEP。
在△DME和△EPF中,
∠DME=∠EPF,EM=EP,∠DEM=∠FEP,
∴△DME≌△EPF(ASA),
∴DE=EF。
∵四边形DEFG是矩形,
∴矩形DEFG是正方形。
(2)解:四边形CEDG的面积是定值,定值为1。
∵四边形DEFG是正方形,
∴DE=DG,∠EDG=90°。
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE+∠EDC=∠CDG+∠EDC=90°,
∴∠ADE=∠CDG。
在△ADE和△CDG中,
AD=CD,∠ADE=∠CDG,DE=DG,
∴△ADE≌△CDG(SAS),
∴S△ADE=S△CDG。
∵S四边形CEDG=S△CDE+S△CDG=S△CDE+S△ADE=S△ADC,
∵AB=√2,正方形ABCD中,AC=√2AB=2,AD=CD=√2,
S△ADC=1/2×AD×CD=1/2×√2×√2=1,
∴四边形CEDG的面积为1。
查看更多完整答案,请扫码查看


