2025年本土假期作业巩固训练八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年本土假期作业巩固训练八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
19. 某校在学生体检结束后,运用简单随机抽样方法抽取了10名学生的身高(单位:cm),记录如下样本数据:145,155,175,165,180,164,166,170,165,165. 请你计算该样本数据的中位数和众数.
答案:
【解析】:
本题主要考察中位数和众数的计算。
中位数:将一组数据从小到大(或从大到小)排列,如果数据量为奇数,则中位数是中间的那个数;
如果数据量为偶数,则中位数是中间两个数的平均值。
众数:一组数据中出现次数最多的数。
首先,我们将给定的样本数据从小到大排列:
$145, 155, 164, 165, 165, 165, 166, 170, 175, 180$,
由于数据量为偶数(10个),所以中位数是第5个和第6个数据的平均值,即:
$(165 + 165) ÷ 2 = 165(cm)$,
接着,我们观察数据,发现$165cm$出现了3次,是出现次数最多的数,所以众数为$165cm$。
【答案】:
中位数为$165cm$,众数为$165cm$。
本题主要考察中位数和众数的计算。
中位数:将一组数据从小到大(或从大到小)排列,如果数据量为奇数,则中位数是中间的那个数;
如果数据量为偶数,则中位数是中间两个数的平均值。
众数:一组数据中出现次数最多的数。
首先,我们将给定的样本数据从小到大排列:
$145, 155, 164, 165, 165, 165, 166, 170, 175, 180$,
由于数据量为偶数(10个),所以中位数是第5个和第6个数据的平均值,即:
$(165 + 165) ÷ 2 = 165(cm)$,
接着,我们观察数据,发现$165cm$出现了3次,是出现次数最多的数,所以众数为$165cm$。
【答案】:
中位数为$165cm$,众数为$165cm$。
20. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分100分). 他们的各项成绩如下表所示:
|候选人|笔试成绩/分|面试成绩分|
|甲|90|88|
|乙|84|92|
|丙|x|90|
|丁|88|86|
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
|候选人|笔试成绩/分|面试成绩分|
|甲|90|88|
|乙|84|92|
|丙|x|90|
|丁|88|86|
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
答案:
(1) 将面试成绩按从小到大排序:86,88,90,92
中位数为 $\frac{88 + 90}{2} = 89$
(2) 解:由题意得 $60\%x + 40\% × 90 = 87.6$
$0.6x + 36 = 87.6$
$0.6x = 51.6$
$x = 86$
(3) 甲的综合成绩:$90 × 60\% + 88 × 40\% = 54 + 35.2 = 89.2$
乙的综合成绩:$84 × 60\% + 92 × 40\% = 50.4 + 36.8 = 87.2$
丁的综合成绩:$88 × 60\% + 86 × 40\% = 52.8 + 34.4 = 87.2$
排序:甲(89.2) > 丙(87.6) > 乙(87.2) = 丁(87.2)
前两名:甲、丙
(1) 将面试成绩按从小到大排序:86,88,90,92
中位数为 $\frac{88 + 90}{2} = 89$
(2) 解:由题意得 $60\%x + 40\% × 90 = 87.6$
$0.6x + 36 = 87.6$
$0.6x = 51.6$
$x = 86$
(3) 甲的综合成绩:$90 × 60\% + 88 × 40\% = 54 + 35.2 = 89.2$
乙的综合成绩:$84 × 60\% + 92 × 40\% = 50.4 + 36.8 = 87.2$
丁的综合成绩:$88 × 60\% + 86 × 40\% = 52.8 + 34.4 = 87.2$
排序:甲(89.2) > 丙(87.6) > 乙(87.2) = 丁(87.2)
前两名:甲、丙
21. 八(1)班组织了一次食品安全知识竞赛,甲、乙两队各5人的成绩如下表所示(10分制).
|甲|8|10|9|6|9|
|乙|10|8|9|7|8|
(1)甲队成绩的中位数是
(2)乙队成绩的众数是
(3)分别计算甲队、乙队成绩的方差,并判断哪队的成绩更稳定?为什么?
|甲|8|10|9|6|9|
|乙|10|8|9|7|8|
(1)甲队成绩的中位数是
9
分;(2)乙队成绩的众数是
8
分;(3)分别计算甲队、乙队成绩的方差,并判断哪队的成绩更稳定?为什么?
解:甲队平均成绩:$\overline{x}_{甲}=\frac{8+10+9+6+9}{5}=8.4$
甲队方差:$s^{2}_{甲}=\frac{1}{5}[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]$
$=\frac{1}{5}[0.16+2.56+0.36+5.76+0.36]=1.84$
乙队平均成绩:$\overline{x}_{乙}=\frac{10+8+9+7+8}{5}=8.4$
乙队方差:$s^{2}_{乙}=\frac{1}{5}[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]$
$=\frac{1}{5}[2.56+0.16+0.36+1.96+0.16]=1.04$
$\because 1.04<1.84$,$\therefore$乙队成绩更稳定.
甲队方差:$s^{2}_{甲}=\frac{1}{5}[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]$
$=\frac{1}{5}[0.16+2.56+0.36+5.76+0.36]=1.84$
乙队平均成绩:$\overline{x}_{乙}=\frac{10+8+9+7+8}{5}=8.4$
乙队方差:$s^{2}_{乙}=\frac{1}{5}[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]$
$=\frac{1}{5}[2.56+0.16+0.36+1.96+0.16]=1.04$
$\because 1.04<1.84$,$\therefore$乙队成绩更稳定.
答案:
(1)9
(2)8
(3)解:甲队平均成绩:$\overline{x}_{甲}=\frac{8+10+9+6+9}{5}=8.4$
甲队方差:$s^{2}_{甲}=\frac{1}{5}[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]$
$=\frac{1}{5}[0.16+2.56+0.36+5.76+0.36]=1.84$
乙队平均成绩:$\overline{x}_{乙}=\frac{10+8+9+7+8}{5}=8.4$
乙队方差:$s^{2}_{乙}=\frac{1}{5}[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]$
$=\frac{1}{5}[2.56+0.16+0.36+1.96+0.16]=1.04$
$\because 1.04<1.84$,$\therefore$乙队成绩更稳定.
(1)9
(2)8
(3)解:甲队平均成绩:$\overline{x}_{甲}=\frac{8+10+9+6+9}{5}=8.4$
甲队方差:$s^{2}_{甲}=\frac{1}{5}[(8-8.4)^{2}+(10-8.4)^{2}+(9-8.4)^{2}+(6-8.4)^{2}+(9-8.4)^{2}]$
$=\frac{1}{5}[0.16+2.56+0.36+5.76+0.36]=1.84$
乙队平均成绩:$\overline{x}_{乙}=\frac{10+8+9+7+8}{5}=8.4$
乙队方差:$s^{2}_{乙}=\frac{1}{5}[(10-8.4)^{2}+(8-8.4)^{2}+(9-8.4)^{2}+(7-8.4)^{2}+(8-8.4)^{2}]$
$=\frac{1}{5}[2.56+0.16+0.36+1.96+0.16]=1.04$
$\because 1.04<1.84$,$\therefore$乙队成绩更稳定.
22. 某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序是:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试,两个程序的结果统计如下:
| |测试成绩/分|
| |甲|乙|丙|
|笔试|92|90|95|
|面试|85|95|80|
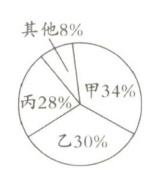
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
| |测试成绩/分|
| |甲|乙|丙|
|笔试|92|90|95|
|面试|85|95|80|

请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
答案:
【解析】:本题可根据扇形统计图中各部分所占百分比来计算甲、乙、丙的得票数,再根据加权平均数的计算公式分别计算甲、乙、丙三人的总成绩,进而确定被推荐的学生。
(1)计算甲、乙、丙的得票数:
已知全年级有$200$名学生,每名学生只能给一名候选人投票,从扇形统计图可知甲、乙、丙得票所占的百分比分别为$34\%$、$30\%$、$28\%$。
根据“部分数量 = 总体数量×部分所占百分比”,分别计算甲、乙、丙的得票数:
甲的得票数:$200×34\% = 200×0.34 = 68$(票);
乙的得票数:$200×30\% = 200×0.3 = 60$(票);
丙的得票数:$200×28\% = 200×0.28 = 56$(票)。
(2)计算甲、乙、丙三人的总成绩并确定被推荐的学生:
已知投票、笔试、面试三项得分按照$2:5:3$的比例计入每名候选人的总成绩,根据加权平均数的计算公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$(其中$\overline{x}$为加权平均数,$x_{i}$为各数据,$f_{i}$为各数据的权数)分别计算甲、乙、丙三人的总成绩。
甲的总成绩:
投票得分:$68×2 = 136$(分);
笔试得分:$92×5 = 460$(分);
面试得分:$85×3 = 255$(分);
总成绩:$\frac{136 + 460 + 255}{2 + 5 + 3}=\frac{851}{10}= 85.1$(分)。
乙的总成绩:
投票得分:$60×2 = 120$(分);
笔试得分:$90×5 = 450$(分);
面试得分:$95×3 = 285$(分);
总成绩:$\frac{120 + 450 + 285}{2 + 5 + 3}=\frac{855}{10}= 85.5$(分)。
丙的总成绩:
投票得分:$56×2 = 112$(分);
笔试得分:$95×5 = 475$(分);
面试得分:$80×3 = 240$(分);
总成绩:$\frac{112 + 475 + 240}{2 + 5 + 3}=\frac{827}{10}= 82.7$(分)。
比较三人的总成绩:$85.5\gt 85.1\gt 82.7$,即乙的总成绩最高。
【答案】:
(1)甲的得票数为$68$票,乙的得票数为$60$票,丙的得票数为$56$票;
(2)乙将被推荐。
(1)计算甲、乙、丙的得票数:
已知全年级有$200$名学生,每名学生只能给一名候选人投票,从扇形统计图可知甲、乙、丙得票所占的百分比分别为$34\%$、$30\%$、$28\%$。
根据“部分数量 = 总体数量×部分所占百分比”,分别计算甲、乙、丙的得票数:
甲的得票数:$200×34\% = 200×0.34 = 68$(票);
乙的得票数:$200×30\% = 200×0.3 = 60$(票);
丙的得票数:$200×28\% = 200×0.28 = 56$(票)。
(2)计算甲、乙、丙三人的总成绩并确定被推荐的学生:
已知投票、笔试、面试三项得分按照$2:5:3$的比例计入每名候选人的总成绩,根据加权平均数的计算公式$\overline{x}=\frac{x_{1}f_{1}+x_{2}f_{2}+\cdots +x_{n}f_{n}}{f_{1}+f_{2}+\cdots +f_{n}}$(其中$\overline{x}$为加权平均数,$x_{i}$为各数据,$f_{i}$为各数据的权数)分别计算甲、乙、丙三人的总成绩。
甲的总成绩:
投票得分:$68×2 = 136$(分);
笔试得分:$92×5 = 460$(分);
面试得分:$85×3 = 255$(分);
总成绩:$\frac{136 + 460 + 255}{2 + 5 + 3}=\frac{851}{10}= 85.1$(分)。
乙的总成绩:
投票得分:$60×2 = 120$(分);
笔试得分:$90×5 = 450$(分);
面试得分:$95×3 = 285$(分);
总成绩:$\frac{120 + 450 + 285}{2 + 5 + 3}=\frac{855}{10}= 85.5$(分)。
丙的总成绩:
投票得分:$56×2 = 112$(分);
笔试得分:$95×5 = 475$(分);
面试得分:$80×3 = 240$(分);
总成绩:$\frac{112 + 475 + 240}{2 + 5 + 3}=\frac{827}{10}= 82.7$(分)。
比较三人的总成绩:$85.5\gt 85.1\gt 82.7$,即乙的总成绩最高。
【答案】:
(1)甲的得票数为$68$票,乙的得票数为$60$票,丙的得票数为$56$票;
(2)乙将被推荐。
查看更多完整答案,请扫码查看


