《2025年本土假期作业巩固训练八年级数学》

1. 下列性质中,矩形不一定具有的是 (A)
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.邻边互相垂直

答案： 【解析】：
本题主要考察矩形的性质。
矩形是一个四边形，其中相对的两边平行且等长，每个角都是直角。
A. 对于矩形的对角线，它们是相等的，但并不一定互相垂直。只有在矩形是正方形的情况下，对角线才互相垂直。因此，A选项是矩形不一定具有的性质。
B. 矩形的对角线是相等的，这是矩形的一个基本性质。
C. 矩形的对角线不仅相等，而且互相平分。这也是矩形的一个基本性质。
D. 矩形的邻边是互相垂直的，因为矩形的每个角都是直角。
综上所述，矩形不一定具有的性质是对角线互相垂直。
【答案】：
A

2. 如图,矩形 ABCD 的对角线 AC= 4,∠BOA= 120°,则 AB 的长是 (C)
A.√3
B.2
C.2√3
D.4

答案： 解：
∵四边形ABCD是矩形，
∴AC=BD=4，OA=OC=AC/2=2，OB=OD=BD/2=2，
∴OA=OB=2，
∵∠BOA=120°，
∴∠OAB=∠OBA=(180°-120°)/2=30°，
过点O作OE⊥AB于点E，
则AE=BE=AB/2，
在Rt△AOE中，∠OAE=30°，OA=2，
∴OE=OA/2=1，
∴AE=√(OA²-OE²)=√(2²-1²)=√3，
∴AB=2AE=2√3。
答案：C

3. 如图,在矩形 ABCD 中,AB= 2,BC= 4,对角线 AC 的垂直平分线分别交 AD,AC 于点 E,O,连结 CE,则 CE= (D)

A.3
B.3.5
C.2.8
D.2.5

答案： 【解析】：
本题主要考查了矩形的性质以及线段垂直平分线的性质。
首先，由于ABCD是矩形，所以$AB = CD = 2$，$BC = AD = 4$，且$\angle B = 90^\circ$。
接着，由于EF是AC的垂直平分线，根据垂直平分线的性质，有$AE = CE$。
设$CE = x$，则$AE = x$，$ED = AD - AE = 4 - x$。
在直角三角形CDE中，根据勾股定理，有
$CD^2 + ED^2 = CE^2$
即
$2^2 + (4 - x)^2 = x^2$
$4 + 16 - 8x + x^2 = x^2$
$20 - 8x = 0$
$8x = 20$
$x = 2.5$
所以，$CE = 2.5$。
【答案】：D. $2.5$。

4. 如图,矩形 ABCD 和矩形 BDEF,点 A 在 EF 边上,设矩形 ABCD 和矩形 BDEF 的面积分别为$ S_1,S_2,$则$ S_1 $与$ S_2 $的大小关系为 (A)
A. $ S_1= S_2 $ B. $ S_1＞S_2 $ C. $ S_1＜S_2 $ D. $ 3S_1= 2S_2 $

答案： 解：连接BD。
∵四边形ABCD是矩形，
∴S₁=AB×AD=2S△ABD。
∵四边形BDEF是矩形，点A在EF上，
∴EF//BD，S₂=BD×高（EF与BD间距离）=2S△ABD。
∴S₁=S₂。
A

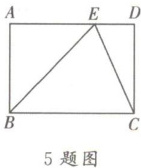
5. 如图,在矩形 ABCD 中,点 E 在 AD 上,且 EC 平分∠BED,AB= 2,∠ABE= 45°,则 DE 的长为$2\sqrt{2} - 2$.

答案： 【解析】：
本题主要考查了矩形的性质、等腰直角三角形的判定与性质以及角平分线的性质。
首先，由于ABCD是矩形，所以$\angle A = 90^\circ$，$AD // BC$。
由于$\angle ABE = 45^\circ$，且$AB = 2$，根据等腰直角三角形的性质，我们可以得出$AE = AB = 2$。
由于$AD // BC$，根据平行线的性质，我们有$\angle DEC = \angle BCE$。
又因为$EC$平分$\angle BED$，所以$\angle BEC = \angle DEC$。
由于$\angle DEC = \angle BCE$且$\angle BEC = \angle DEC$，我们可以得出$\angle BEC = \angle BCE$，从而$BE = BC$。
由于ABCD是矩形，所以$BC = AD$，结合前面的步骤，我们得出$BE = AD$。
设$DE = x$，则$AD = AE + DE = 2 + x$。
由于$BE = BC = AD$，我们可以在直角三角形$ABE$中使用勾股定理来求解$BE$，即$BE = \sqrt{AB^2 + AE^2} = \sqrt{2^2 + 2^2} = 2\sqrt{2}$。
因此，$AD = 2\sqrt{2}$，所以$DE = AD - AE = 2\sqrt{2} - 2$。
【答案】：
$2\sqrt{2} - 2$。

6. 如图,在矩形 ABCD 中,AB= 12,AD= 10,点 P 在 AD 上,点 Q 在 BC 上,且 AP= CQ,连结 CP,QD,则 PC+QD 的最小值为____.

26

答案： 解：在矩形ABCD中，AD=BC=10，AB=CD=12，AD//BC。
设AP=CQ=x，则PD=AD-AP=10-x，BQ=BC-CQ=10-x，所以PD=BQ。
∵PD//BQ，
∴四边形PDQB是平行四边形，
∴QD=PB。
∴PC+QD=PC+PB，即求PC+PB的最小值。
作点C关于AD的对称点C'，则PC=PC'，
∴PC+PB=PC'+PB。
当点P、B、C'三点共线时，PC'+PB最小，最小值为BC'的长。
∵点C与C'关于AD对称，AD⊥CD，
∴CC'=2CD=24，且CC'⊥CD。
在Rt△BCC'中，BC=10，CC'=24，
∴BC'=$\sqrt{BC^2 + CC'^2}=\sqrt{10^2 + 24^2}=\sqrt{100 + 576}=\sqrt{676}=26$。
即PC+QD的最小值为26。
26

7. 如图,在矩形 ABCD 中,对角线 AC,BD 交于点 O,过点 C 作 CE//BD,交 AD 的延长线于点 E.
(1)求证:AC= CE;
(2)若 DE= 9,CD= 12,求△COD 的周长.

答案： 【解析】：
(1)本题可通过证明四边形$BDEC$是平行四边形，得到$BD = CE$，再结合矩形的性质$AC = BD$，进而证明$AC = CE$。
(2)要求$\triangle COD$的周长，需要先求出$OC$、$OD$、$CD$的长度，已知$CD$的长度，可根据矩形的性质得到$BD$与$AC$的关系，再结合$DE$的长度求出$BD$的长度，进而求出$OC$、$OD$的长度。
【答案】：
(1)证明：
∵四边形$ABCD$是矩形，
∴$AD// BC$，$AC = BD$。
∵$CE// BD$，$DE// BC$（$AD$的延长线），
∴四边形$BDEC$是平行四边形（两组对边分别平行的四边形是平行四边形）。
∴$BD = CE$（平行四边形的对边相等）。
∵$AC = BD$，
∴$AC = CE$。
(2)解：
∵四边形$BDEC$是平行四边形，
∴$BD = CE$，$DE = BC$。
∵$DE = 9$，
∴$BC = 9$。
∵四边形$ABCD$是矩形，
∴$AC = BD$，$OA = OC=\frac{1}{2}AC$，$OB = OD=\frac{1}{2}BD$（矩形的对角线相等且互相平分）。
∴$OC = OD$。
在$Rt\triangle BCD$中，$BC = 9$，$CD = 12$，根据勾股定理$BD=\sqrt{BC^{2}+CD^{2}}$，可得：
$BD=\sqrt{9^{2}+12^{2}}=\sqrt{81 + 144}=\sqrt{225}=15$。
∴$OC = OD=\frac{1}{2}BD=\frac{15}{2}$。
∴$\triangle COD$的周长为：$OC + OD + CD=\frac{15}{2}+\frac{15}{2}+12 = 15 + 12 = 27$。
综上，$\triangle COD$的周长为$27$。