《2025年本土假期作业巩固训练八年级数学》

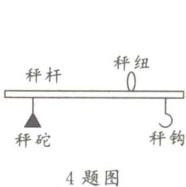
4. 秤是我国传统的计重工具。如图,可以用秤砣到秤纽的水平距离,来得出秤钩上所挂物体的重量。称重时,秤钩所挂物重为$y$(斤)是秤杆上秤砣到秤纽的水平距离$x$(厘米)的一次函数。下表中为若干次称重时所记录的一些数据：
|$x$(厘米)|$1$|$3$|$4$|$6$|$11$|$12$|
|$y$(斤)|$0.75$|$1.25$|$1.50$|$2.25$|$3.25$|$3.50$|
其中有一个$y$值记录错误,请排除后,利用正确数据确定当$x = 24$厘米时,对应的$y$为____斤。

6.5

答案： 解：设一次函数解析式为$y = kx + b$。
选取$x=1$，$y=0.75$和$x=3$，$y=1.25$代入得：
$\begin{cases}0.75 = k + b \\1.25 = 3k + b\end{cases}$
解得$k=0.25$，$b=0.5$，函数解析式为$y=0.25x + 0.5$。
检验其他数据：
当$x=4$时，$y=0.25×4 + 0.5=1.50$，正确；
当$x=6$时，$y=0.25×6 + 0.5=2.00≠2.25$，错误；
当$x=11$时，$y=0.25×11 + 0.5=3.25$，正确；
当$x=12$时，$y=0.25×12 + 0.5=3.50$，正确。
当$x=24$时，$y=0.25×24 + 0.5=6.5$。
6.5

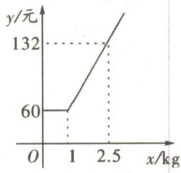
5. 春暖花开,正是踏青采摘的好时节,小远周末和家人一起去秦岭脚下采摘园采摘草莓。现有甲、乙两家草莓采摘园,两家草莓的品种品质相同,售价均为 60 元/kg。两家分别推出了不同的优惠方案：甲采摘园：9 折优惠；乙采摘园的采摘重量$x$(kg)和价格$y$(元)之间的关系如图所示。
设小远和家人采摘草莓$x$ kg,在甲、乙采摘园采摘所需费用分别是$y_{甲}和y_{乙}$。
(1)请你分别写出$y_{甲}和y_{乙}与x$的函数关系式；
(2)请你帮助小远分析,去哪一家采摘园采摘草莓更合算。

答案： 【解析】：
(1)这一问主要考查根据题目条件列出函数关系式。对于甲采摘园，已知售价为$60$元$/kg$，且有$9$折优惠，那么每千克草莓的实际价格就是$60×0.9 = 54$元，所以$y_{甲}$与$x$的函数关系式为$y_{甲}=54x$。
对于乙采摘园，需要根据图象来分析。当$0\lt x\leq1$时，从图象可以看出价格$y_{乙}$恒定为$60$元，所以$y_{乙}=60x$（此时$x$的系数就是单价）；当$x\gt1$时，设$y_{乙}=kx+b$（$k\neq0$），利用图象上的两个点$(1, 60)$和$(2.5, 132)$来求解$k$和$b$。将点代入$y_{乙}=kx+b$得到方程组$\begin{cases}k + b = 60\\2.5k + b = 132\end{cases}$，用第二个方程减去第一个方程消去$b$可得：$2.5k + b -(k + b)=132 - 60$，即$1.5k = 72$，解得$k = 48$，再将$k = 48$代入$k + b = 60$，可得$48 + b = 60$，解得$b = 12$，所以当$x\gt1$时，$y_{乙}=48x + 12$。
(2)这一问主要考查通过比较两个函数的大小来解决实际问题。需要分三种情况讨论：
当$y_{甲}\lt y_{乙}$时，即$54x\lt48x + 12$，解这个不等式：$54x - 48x\lt12$，$6x\lt12$，得到$x\lt2$，结合$x$的取值范围$x\gt0$以及乙采摘园分段函数的情况，此时$0\lt x\lt2$。
当$y_{甲}=y_{乙}$时，即$54x = 48x + 12$，解方程：$54x - 48x = 12$，$6x = 12$，得到$x = 2$。
当$y_{甲}\gt y_{乙}$时，即$54x\gt48x + 12$，解不等式：$54x - 48x\gt12$，$6x\gt12$，得到$x\gt2$。
【答案】：
(1)$y_{甲}=54x$；当$0\lt x\leq1$时，$y_{乙}=60x$，当$x\gt1$时，$y_{乙}=48x + 12$。
(2)当$0\lt x\lt2$时，去甲采摘园更合算；当$x = 2$时，去甲、乙两家采摘园一样；当$x\gt2$时，去乙采摘园更合算。

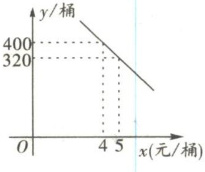
6. 某校八年级(1)班共有学生 50 人,据统计,原来每人每年用于购买饮料的平均支出是$a$元。经测算和市场调查,若该班学生集体改饮某品牌的桶装纯净水,则年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用 780 元,其中,纯净水的销售价$x$(元/桶)与年购买总量$y$(桶)之间满足如图所示关系。
(1)求$y与x$的函数关系式；
(2)若该班每年需要纯净水 380 桶,且$a$为 120 时,请你根据提供的信息分析一下：该班学生集体改饮桶装纯净水与个人买饮料,哪一种花钱更少？
(3)求该班每年购买纯净水费用的最大值,并指出当$a$至少为多少时,该班学生集体改饮桶装纯净水更合算。

答案：
(1)设$y$与$x$的函数关系式为$y=kx+b$，由图可知函数过点$(4,400)$和$(5,320)$，则$\begin{cases}4k+b=400\\5k+b=320\end{cases}$，解得$\begin{cases}k=-80\\b=720\end{cases}$，所以$y=-80x+720$。
(2)当$y=380$时，$380=-80x+720$，解得$x=4.25$，年总费用为$380×4.25 + 780 = 1615 + 780 = 2395$元。个人买饮料总费用为$50×120 = 6000$元，因为$2395＜6000$，所以集体改饮桶装纯净水花钱更少。
(3)购买纯净水费用$W=xy=x(-80x + 720)=-80x^2 + 720x=-80(x - 4.5)^2 + 1620$，当$x=4.5$时，$W$最大值为$1620$元。要集体改饮更合算，则$-80x^2 + 720x + 780 ＜ 50a$，由$W$最大值$1620$，得$1620 + 780 ＜ 50a$，即$2400 ＜ 50a$，解得$a ＞ 48$，所以$a$至少为$49$时更合算。
(1)函数关系式为$y=-80x+720$；
(2)集体改饮桶装纯净水花钱更少；
(3)最大值为$1620$元，$a$至少为$49$。