2025年本土假期作业巩固训练八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年本土假期作业巩固训练八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
10. 甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠。乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售。活动期间,某顾客的草莓采摘量为$x$千克,若在甲园采摘需总费用$y_{1}$元,若在乙园采摘需总费用$y_{2}$元。$y_{1}$,$y_{2}与x$之间的函数图象如图所示,则下列说法中错误的是( )
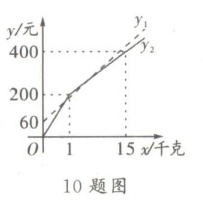
A.甲园的门票费用是 60 元
B.草莓优惠前的销售价格是 40 元/千克
C.乙园超过 5 千克后,超过的部分价格优惠是打五折
D.若顾客采摘 15 千克草莓,那么到甲园比到乙园采摘更实惠
C

A.甲园的门票费用是 60 元
B.草莓优惠前的销售价格是 40 元/千克
C.乙园超过 5 千克后,超过的部分价格优惠是打五折
D.若顾客采摘 15 千克草莓,那么到甲园比到乙园采摘更实惠
答案:
解:A. 当x=0时,y₁=60,故甲园门票60元,A正确。
B. 设草莓原价为m元/千克,甲园y₁=0.6mx+60。由图知x=5时,y₁=180,代入得180=0.6m×5+60,解得m=40,B正确。
C. 乙园:0≤x≤5时,y₂=40x;x=5时,y₂=200。设超过5千克后,y₂=kx+b,由图知x=10时,y₂=380,代入得{200=5k+b,380=10k+b},解得k=36,b=20。超过部分单价36元,36÷40=0.9,即九折,C错误。
D. 甲园:y₁=0.6×40×15+60=420元。乙园:y₂=36×15+20=560元。420<560,D正确。
答案:C
B. 设草莓原价为m元/千克,甲园y₁=0.6mx+60。由图知x=5时,y₁=180,代入得180=0.6m×5+60,解得m=40,B正确。
C. 乙园:0≤x≤5时,y₂=40x;x=5时,y₂=200。设超过5千克后,y₂=kx+b,由图知x=10时,y₂=380,代入得{200=5k+b,380=10k+b},解得k=36,b=20。超过部分单价36元,36÷40=0.9,即九折,C错误。
D. 甲园:y₁=0.6×40×15+60=420元。乙园:y₂=36×15+20=560元。420<560,D正确。
答案:C
11. 在函数$y = \frac{\sqrt{1 - x}}{x + 2}$中,自变量$x$的取值范围是
$x \leq 1$ 且 $x \neq -2$
。
答案:
【解析】:
本题主要考查了函数自变量的取值范围问题。
对于二次根式,被开方数必须大于等于0;
对于分式,分母不能为0。
因此,我们需要满足以下两个条件:
$1 - x \geq 0$ ,以确保二次根式内的表达式非负。
$x + 2 \neq 0$,以确保分母不为0。
解第一个不等式 $1 - x \geq 0$,得到 $x \leq 1$。
解第二个不等式 $x + 2 \neq 0$,得到 $x \neq -2$。
综合以上两个条件,我们得到自变量 $x$ 的取值范围是 $x \leq 1$ 且 $x \neq -2$。
【答案】:
$x \leq 1$ 且 $x \neq -2$。
本题主要考查了函数自变量的取值范围问题。
对于二次根式,被开方数必须大于等于0;
对于分式,分母不能为0。
因此,我们需要满足以下两个条件:
$1 - x \geq 0$ ,以确保二次根式内的表达式非负。
$x + 2 \neq 0$,以确保分母不为0。
解第一个不等式 $1 - x \geq 0$,得到 $x \leq 1$。
解第二个不等式 $x + 2 \neq 0$,得到 $x \neq -2$。
综合以上两个条件,我们得到自变量 $x$ 的取值范围是 $x \leq 1$ 且 $x \neq -2$。
【答案】:
$x \leq 1$ 且 $x \neq -2$。
12. 已知$M(x_{1},y_{1})$,$N(x_{2},y_{2})$两点都在反比例函数$y = \frac{-5}{x}$的图象上,且$x_{1} > 0 > x_{2}$,则$y_{1}$
<
$y_{2}$。(选填“>”“<”或“=”)
答案:
【解析】:
本题主要考察反比例函数$y = \frac{-5}{x}$的性质。
反比例函数$y = \frac{-5}{x}$中,因为系数$k = -5 < 0$,所以该函数的图像位于第二,四象限。
根据题目条件,$x_1 > 0$,所以点$M(x_1, y_1)$位于第四象限,因此$y_1 < 0$;
同样,$x_2 < 0$,所以点$N(x_2, y_2)$位于第二象限,因此$y_2 > 0$。
由于$y_1 < 0$且$y_2 > 0$,可以得出$y_1 < y_2$。
【答案】:
$<$
本题主要考察反比例函数$y = \frac{-5}{x}$的性质。
反比例函数$y = \frac{-5}{x}$中,因为系数$k = -5 < 0$,所以该函数的图像位于第二,四象限。
根据题目条件,$x_1 > 0$,所以点$M(x_1, y_1)$位于第四象限,因此$y_1 < 0$;
同样,$x_2 < 0$,所以点$N(x_2, y_2)$位于第二象限,因此$y_2 > 0$。
由于$y_1 < 0$且$y_2 > 0$,可以得出$y_1 < y_2$。
【答案】:
$<$
13. 已知正比例函数$y = ax与反比例函数y = \frac{b}{x}的图象交于点A(m,n)$,则这两个函数图象的另一个交点为
$(-m,-n)$
。
答案:
【解析】:
本题主要考查正比例函数和反比例函数交点的性质,即它们的交点关于原点对称。
由于正比例函数$y=ax$和反比例函数$y=\frac{b}{x}$的图像都关于原点对称,
因此,如果$(m,n)$是它们的一个交点,
那么关于原点对称的点$(-m,-n)$也必然是它们的一个交点。
我们可以根据两个函数在点A处的函数值相等来验证这一点。
对于正比例函数,有$n=am$,
对于反比例函数,有$n=\frac{b}{m}$,
由于两个函数在点A处的函数值相等,我们可以得到:
$am=\frac{b}{m}$
即$b=am^2$
这是两个函数在点A处相交的条件。
现在,我们考虑另一个交点$(-m,-n)$,
对于正比例函数,有$-n=a(-m)$,即$n=am$,满足正比例函数的定义。
对于反比例函数,有$-n=\frac{b}{-m}$,即$n=\frac{b}{m}$,满足反比例函数的定义。
由于$b=am^2$,我们可以验证在点$(-m,-n)$处,两个函数的函数值仍然相等,
因此,点$(-m,-n)$是正比例函数和反比例函数的另一个交点。
【答案】:$(-m,-n)$
本题主要考查正比例函数和反比例函数交点的性质,即它们的交点关于原点对称。
由于正比例函数$y=ax$和反比例函数$y=\frac{b}{x}$的图像都关于原点对称,
因此,如果$(m,n)$是它们的一个交点,
那么关于原点对称的点$(-m,-n)$也必然是它们的一个交点。
我们可以根据两个函数在点A处的函数值相等来验证这一点。
对于正比例函数,有$n=am$,
对于反比例函数,有$n=\frac{b}{m}$,
由于两个函数在点A处的函数值相等,我们可以得到:
$am=\frac{b}{m}$
即$b=am^2$
这是两个函数在点A处相交的条件。
现在,我们考虑另一个交点$(-m,-n)$,
对于正比例函数,有$-n=a(-m)$,即$n=am$,满足正比例函数的定义。
对于反比例函数,有$-n=\frac{b}{-m}$,即$n=\frac{b}{m}$,满足反比例函数的定义。
由于$b=am^2$,我们可以验证在点$(-m,-n)$处,两个函数的函数值仍然相等,
因此,点$(-m,-n)$是正比例函数和反比例函数的另一个交点。
【答案】:$(-m,-n)$
14. 如图,一直线与两坐标轴的正半轴分别交于$A$,$B$两点,$P是线段AB$上任意一点(不包括端点),过$P$分别作两坐标轴的垂线,与两坐标轴围成的矩形的周长为 10,则该直线的函数表达式是______。
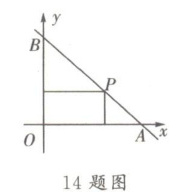

$y = -x + 5$
答案:
【解析】:
本题主要考查了一次函数的应用以及矩形的性质。
设点$P$的坐标为$(x, y)$,由于$P$在线段$AB$上,且$A$,$B$分别为直线与两坐标轴的正半轴的交点,所以$x \gt 0$,$y \gt 0$。
过点$P$分别作两坐标轴的垂线,与两坐标轴围成的矩形,其长为$x$,宽为$y$。
根据矩形的性质,其周长为$2(x + y)$。
由题意知,这个矩形的周长为10,所以有:
$2(x + y) = 10$,
即:
$x + y = 5$,
由于点$P(x, y)$在直线上,且直线过两坐标轴的正半轴交点$A$,$B$,可以设直线的函数表达式为:
$y = kx + b \quad (k \neq 0)$,
由于直线过点$(5,0)$和$(0,5)$(因为当$x=5$时,$y=0$;当$y=5$时,$x=0$,由$x+y=5$得出),可以将这两点的坐标代入直线方程中求解$k$和$b$。
代入点$(5,0)$得:
$0 = 5k + b$,
代入点$(0,5)$得:
$5 = b$,
解这两个方程,得到:
$k = -1$,
$b = 5$,
所以,该直线的函数表达式为:
$y = -x + 5$。
【答案】:
$y = -x + 5$。
本题主要考查了一次函数的应用以及矩形的性质。
设点$P$的坐标为$(x, y)$,由于$P$在线段$AB$上,且$A$,$B$分别为直线与两坐标轴的正半轴的交点,所以$x \gt 0$,$y \gt 0$。
过点$P$分别作两坐标轴的垂线,与两坐标轴围成的矩形,其长为$x$,宽为$y$。
根据矩形的性质,其周长为$2(x + y)$。
由题意知,这个矩形的周长为10,所以有:
$2(x + y) = 10$,
即:
$x + y = 5$,
由于点$P(x, y)$在直线上,且直线过两坐标轴的正半轴交点$A$,$B$,可以设直线的函数表达式为:
$y = kx + b \quad (k \neq 0)$,
由于直线过点$(5,0)$和$(0,5)$(因为当$x=5$时,$y=0$;当$y=5$时,$x=0$,由$x+y=5$得出),可以将这两点的坐标代入直线方程中求解$k$和$b$。
代入点$(5,0)$得:
$0 = 5k + b$,
代入点$(0,5)$得:
$5 = b$,
解这两个方程,得到:
$k = -1$,
$b = 5$,
所以,该直线的函数表达式为:
$y = -x + 5$。
【答案】:
$y = -x + 5$。
15. 若点$M(a + 3,a - 1)$在平面直角坐标系的y轴上,则$a = $
-3
;若点$P(m,n)$的坐标满足$m + n = mn$,则称点$P$为“和谐点”,请写出一个“和谐点”的坐标(2,2)
。
答案:
【解析】:
本题主要考查平面直角坐标系中点的坐标特性及代数方程的求解。
对于点$M(a + 3, a - 1)$在$y$轴上的情况,由于$y$轴上点的横坐标都为0,因此有$a + 3 = 0$,解这个方程即可求出$a$的值。
对于“和谐点”$P(m, n)$,需要满足条件$m + n = mn$。这是一个关于$m$和$n$的二元一次方程,可以通过代数方法求解出满足条件的$m$和$n$的值,从而得到一个“和谐点”的坐标。
【答案】:
解:
由于点$M(a + 3, a - 1)$在$y$轴上,根据$y$轴的性质,其横坐标必须为0,即:
$a + 3 = 0$
解得:
$a = -3$
对于“和谐点”$P(m, n)$,需要满足:
$m + n = mn$
取$m = 2$,代入上式得:
$2 + n = 2n$
解得:
$n = 2$
所以,一个“和谐点”的坐标为$(2, 2)$。(答案不唯一)
故答案为:$a = -3$;一个“和谐点”的坐标为$(2, 2)$(答案不唯一)。
本题主要考查平面直角坐标系中点的坐标特性及代数方程的求解。
对于点$M(a + 3, a - 1)$在$y$轴上的情况,由于$y$轴上点的横坐标都为0,因此有$a + 3 = 0$,解这个方程即可求出$a$的值。
对于“和谐点”$P(m, n)$,需要满足条件$m + n = mn$。这是一个关于$m$和$n$的二元一次方程,可以通过代数方法求解出满足条件的$m$和$n$的值,从而得到一个“和谐点”的坐标。
【答案】:
解:
由于点$M(a + 3, a - 1)$在$y$轴上,根据$y$轴的性质,其横坐标必须为0,即:
$a + 3 = 0$
解得:
$a = -3$
对于“和谐点”$P(m, n)$,需要满足:
$m + n = mn$
取$m = 2$,代入上式得:
$2 + n = 2n$
解得:
$n = 2$
所以,一个“和谐点”的坐标为$(2, 2)$。(答案不唯一)
故答案为:$a = -3$;一个“和谐点”的坐标为$(2, 2)$(答案不唯一)。
16. 星期天,小明上午$8:00$从家里出发,骑车到图书馆去借书,再骑车回到家。他离家的距离$y$(千米)与时间$t$(分钟)的关系如图所示,则上午$8:45$小明离家的距离是
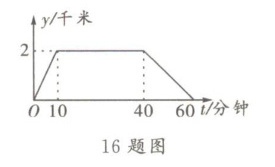
1
千米。
答案:
解:由图可知,小明从家出发到图书馆的过程中,8:00出发,8:30到达图书馆,此时离家距离为4千米,之后开始返回,8:50到家。
上午8:45处于返回阶段,即30分钟到50分钟之间。设返回时距离y与时间t的函数关系式为$y = kt + b$($k \neq 0$)。
当$t = 30$时,$y = 4$;当$t = 50$时,$y = 0$。代入可得:
$\begin{cases}30k + b = 4 \\50k + b = 0\end{cases}$
解得:$k = -\frac{1}{5}$,$b = 10$,所以函数关系式为$y = -\frac{1}{5}t + 10$。
当$t = 45$时,$y = -\frac{1}{5} × 45 + 10 = -9 + 10 = 1$。
1
17. 1896 年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈,这就是有趣的“瞎转圈”现象,经研究,某人蒙上眼睛走出的大圆圈的半径$y$(米)是其两腿迈出的步长之差$x$(厘米)$(x > 0)$的反比例函数,其图象如图所示。若此人蒙上眼睛走出的大圆圈的半径不小于 35 米,则其两腿迈出的步长之差最多是______厘米。
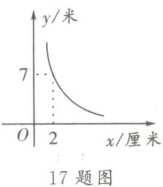

0.4
答案:
【解析】:本题可先根据反比例函数的图象过点$(2,7)$求出反比例函数的表达式,再结合此人蒙上眼睛走出的大圆圈的半径不小于$35$米这一条件,求出两腿迈出的步长之差的最大值。
步骤一:求反比例函数的表达式
设反比例函数的表达式为$y = \frac{k}{x}(k\neq 0)$,因为函数图象过点$(2,7)$,将$x = 2$,$y = 7$代入到$y = \frac{k}{x}$中,可得$7 = \frac{k}{2}$,解得$k = 14$,所以反比例函数的表达式为$y = \frac{14}{x}$。
步骤二:根据条件列不等式并求解
已知此人蒙上眼睛走出的大圆圈的半径不小于$35$米,即$y\geq35$,将$y = \frac{14}{x}$代入$y\geq35$中,得到$\frac{14}{x}\geq35$。
因为$x\gt0$,不等式两边同时乘以$x$,不等号方向不变,可得$14\geq35x$,再两边同时除以$35$,解得$x\leq\frac{14}{35} = 0.4$。
【答案】:$0.4$
步骤一:求反比例函数的表达式
设反比例函数的表达式为$y = \frac{k}{x}(k\neq 0)$,因为函数图象过点$(2,7)$,将$x = 2$,$y = 7$代入到$y = \frac{k}{x}$中,可得$7 = \frac{k}{2}$,解得$k = 14$,所以反比例函数的表达式为$y = \frac{14}{x}$。
步骤二:根据条件列不等式并求解
已知此人蒙上眼睛走出的大圆圈的半径不小于$35$米,即$y\geq35$,将$y = \frac{14}{x}$代入$y\geq35$中,得到$\frac{14}{x}\geq35$。
因为$x\gt0$,不等式两边同时乘以$x$,不等号方向不变,可得$14\geq35x$,再两边同时除以$35$,解得$x\leq\frac{14}{35} = 0.4$。
【答案】:$0.4$
18. 如图,函数$y = \frac{1}{x}(x > 0)和y = \frac{4}{x}的图象分别是l_{1}和l_{2}$,设点$P在l_{2}$上,$PA // y轴交于点A$,$PB // x轴交l_{1}于点B$,$\triangle PAB$的面积为______。


$\frac{9}{8}$
答案:
解:设点P的坐标为$(a,\frac{4}{a})$,其中$a>0$。
因为$PA// y$轴交$l_1$于点A,所以点A的横坐标为$a$。又因为点A在$y=\frac{1}{x}(x>0)$上,所以点A的坐标为$(a,\frac{1}{a})$。
因为$PB// x$轴交$l_1$于点B,所以点B的纵坐标为$\frac{4}{a}$。又因为点B在$y=\frac{1}{x}(x>0)$上,所以$\frac{4}{a}=\frac{1}{x}$,解得$x=\frac{a}{4}$,即点B的坐标为$(\frac{a}{4},\frac{4}{a})$。
则$PA=\vert\frac{4}{a}-\frac{1}{a}\vert=\frac{3}{a}$,$PB=\vert a-\frac{a}{4}\vert=\frac{3a}{4}$。
因为$PA// y$轴,$PB// x$轴,所以$\angle APB=90^\circ$,即$\triangle PAB$是直角三角形。
所以$\triangle PAB$的面积为$\frac{1}{2}× PA× PB=\frac{1}{2}×\frac{3}{a}×\frac{3a}{4}=\frac{9}{8}$。
答案:$\frac{9}{8}$
因为$PA// y$轴交$l_1$于点A,所以点A的横坐标为$a$。又因为点A在$y=\frac{1}{x}(x>0)$上,所以点A的坐标为$(a,\frac{1}{a})$。
因为$PB// x$轴交$l_1$于点B,所以点B的纵坐标为$\frac{4}{a}$。又因为点B在$y=\frac{1}{x}(x>0)$上,所以$\frac{4}{a}=\frac{1}{x}$,解得$x=\frac{a}{4}$,即点B的坐标为$(\frac{a}{4},\frac{4}{a})$。
则$PA=\vert\frac{4}{a}-\frac{1}{a}\vert=\frac{3}{a}$,$PB=\vert a-\frac{a}{4}\vert=\frac{3a}{4}$。
因为$PA// y$轴,$PB// x$轴,所以$\angle APB=90^\circ$,即$\triangle PAB$是直角三角形。
所以$\triangle PAB$的面积为$\frac{1}{2}× PA× PB=\frac{1}{2}×\frac{3}{a}×\frac{3a}{4}=\frac{9}{8}$。
答案:$\frac{9}{8}$
查看更多完整答案,请扫码查看


