《2025年本土假期作业巩固训练八年级数学》

1. 小明在梳理矩形、菱形、正方形的性质时,发现它们的对角线都具有一个共同的性质,这条性质是对角线(A)
A.互相平分
B.相等
C.互相垂直
D.平分一组对角

答案： 【解析】：
本题主要考察矩形、菱形、正方形的性质。
矩形、菱形、正方形都是特殊的平行四边形，因此它们具有平行四边形的所有性质。在平行四边形中，对角线互相平分是一个基本性质。
A. 互相平分：这是平行四边形（包括矩形、菱形、正方形）对角线的一个基本性质。
B. 相等：在矩形和正方形中，对角线相等，但在菱形中，对角线不一定相等。
C. 互相垂直：在菱形和正方形中，对角线互相垂直，但在矩形中，对角线不一定垂直。
D. 平分一组对角：在菱形和正方形中，对角线可以平分一组对角，但在矩形中，这不一定成立。
综上所述，只有“互相平分”是矩形、菱形、正方形对角线都具有的共同性质。
【答案】：
A

2. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离。若AE间的距离调节60cm,菱形的边长AB= 20cm,则∠DAB的度数是(C)
A.90°
B.100°
C.120°
D.150°

答案： 解：连接AE，由三个全等菱形构成，AE间距离为60cm，可得每个菱形在AE方向的对角线长为60÷3=20cm。
菱形ABCD中，AB=20cm，设对角线AC=20cm（沿AE方向）。
菱形对角线互相平分，
∴AO=10cm（O为AC、BD交点）。
在Rt△AOB中，AB=20cm，AO=10cm，
cos∠OAB=AO/AB=10/20=1/2，
∴∠OAB=60°，
则∠DAB=2∠OAB=120°。
答案：C

3. 如图,在平面直角出标系中,正方形OABC的顶点O,B的坐标分边是(0,0),(2,0),则顶点C的坐标是(C)
A.(1,1)
B.(-1,1)
C.(1,-1)
D.(-1,-1)

答案： 1. 首先，设正方形$OABC$的边长为$a$：
已知$O(0,0)$，$B(2,0)$，根据正方形的性质，$OB$是正方形的对角线，由正方形对角线公式$l = \sqrt{2}s$（$l$为对角线长度，$s$为边长），可得$\vert OB\vert=\sqrt{(2 - 0)^2+(0 - 0)^2}=2$，又$\vert OB\vert=\sqrt{2}a$，则$\sqrt{2}a = 2$，解得$a=\sqrt{2}$。
另一种方法：因为正方形$OABC$，设$C(x,y)$，根据正方形的性质，$OC = BC$，且$\angle BOC = 45^{\circ}$。
由$O(0,0)$，$B(2,0)$，根据两点间距离公式$d=\sqrt{(x_2 - x_1)^2+(y_2 - y_1)^2}$，$\vert OC\vert=\sqrt{x^{2}+y^{2}}$，$\vert BC\vert=\sqrt{(x - 2)^2+y^{2}}$，又因为$\vert OC\vert=\vert BC\vert$，所以$\sqrt{x^{2}+y^{2}}=\sqrt{(x - 2)^2+y^{2}}$。
两边平方得$x^{2}+y^{2}=(x - 2)^2+y^{2}$，展开$(x - 2)^2$：$x^{2}+y^{2}=x^{2}-4x + 4+y^{2}$，消去$x^{2}$和$y^{2}$，可得$-4x+4 = 0$，解得$x = 1$。
再根据正方形的性质，$OC$与$x$轴、$y$轴的夹角为$45^{\circ}$，直线$OC$的斜率$k=\tan135^{\circ}=-1$（因为$C$在第四象限），直线$OC$的方程为$y=-x$（过原点$(0,0)$，斜率$k=-1$，根据直线的点 - 斜式方程$y - y_0=k(x - x_0)$，这里$x_0 = 0$，$y_0 = 0$）。
把$x = 1$代入$y=-x$，得$y=-1$。
所以顶点$C$的坐标是$(1,-1)$，答案是C。

4. 如图,矩形ABCD沿AE折叠,使D点落在BC边上的点F处,如果∠BFA= 30°,那么∠CEF的度数是(B)
A.20°
B.30°
C.45°
D.60°

答案： 解：
∵四边形ABCD是矩形，
∴∠B=∠C=∠D=90°，AD=BC，AB=CD。
由折叠性质得：AF=AD，∠AFE=∠D=90°，∠DAE=∠FAE。
在Rt△ABF中，∠BFA=30°，
∴∠BAF=60°，AF=2AB。
∵AD=AF，
∴AD=2AB。
∵∠BAD=90°，∠BAF=60°，
∴∠DAF=∠BAD-∠BAF=30°，
∴∠DAE=∠FAE=15°，∠AEF=90°-∠FAE=75°。
∵∠DEC=180°，
∴∠CEF=180°-∠AEF-∠AED=180°-75°-75°=30°。
答案：B

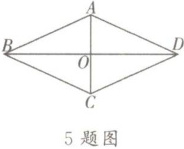
5. 求证：菱形的两条对角线互相垂直。
已知：如图,四边形ABCD是菱形,对角线AC,BD交于点O。
求证：AC⊥BD。
以下是排乱的证明过程：①又BO= DO,②所以AO⊥BD,即AC⊥BD,③因为四边形ABCD是菱形,④所以AB= AD。
证明步骤正确的顺序是(B)

A.③→②→①→④
B.③→④→①→②
C.①→②→④→③
D.①→④→③→②

答案： 【解析】：
首先，我们需要明确题目给出的已知条件和求证目标。
已知条件是四边形ABCD是菱形，对角线AC,BD交于点O。
求证目标是AC⊥BD。
接下来，我们按照逻辑顺序，利用菱形的性质进行推导：
1. 因为四边形ABCD是菱形（根据题目已知条件），所以我们可以得到AB = AD（菱形的四条边相等）。
2. 又因为菱形的对角线互相平分（菱形的性质），所以我们可以得到BO = DO。
3. 接下来，我们连接AB，由于AB = AD，且BO = DO，根据等腰三角形的三线合一性质，我们可以推导出AO是BD的中垂线，即AO⊥BD。
4. 由于AO是AC的一部分，所以我们可以得到AC⊥BD。
因此，我们可以确定证明步骤的正确顺序是：先根据菱形性质得到AB = AD，再根据菱形对角线性质得到BO = DO，然后利用等腰三角形的三线合一性质得到AO⊥BD，最后得出AC⊥BD。
【答案】：
B

6. 如图,在△ABC中,AC= BC,D,E分别是边AB,AC的中点,△ADE≌△CFE,则四边形ADCF一定是(B)
A.菱形
B.矩形
C.正方形

D.无法确定

答案： 解：
∵△ADE≌△CFE，
∴AD=CF，∠A=∠ECF，
∴AD//CF，
∴四边形ADCF是平行四边形.
∵AC=BC，D是AB中点，
∴CD⊥AB（等腰三角形三线合一），
∴∠ADC=90°，
∴平行四边形ADCF是矩形.
答案：B

7. 如图,在□ABCD中,E,F分别为边AD,BC的中点,点G,H在AC上,且AH= CG,若添加一个条件使四边形EGFH是菱形,则下列可以添加的条件是(B)

A.AB= AD
B.AB⊥AD
C.AB= AC
D.AB⊥AC

答案： 解：
∵四边形ABCD是平行四边形，
∴AD=BC，AD//BC，∠EAG=∠FCH。
∵E，F分别为AD，BC中点，
∴AE=CF。
∵AH=CG，AC=CA，
∴AG=CH。
在△AEG和△CFH中，
AE=CF，∠EAG=∠FCH，AG=CH，
∴△AEG≌△CFH（SAS），
∴EG=FH，∠AGE=∠CHF，
∴∠EGH=∠FHG，
∴EG//FH，
∴四边形EGFH是平行四边形。
要使四边形EGFH是菱形，需添加条件使邻边相等或对角线垂直。
选项B：AB⊥AD，
∵AB⊥AD，四边形ABCD是平行四边形，
∴□ABCD是矩形，
∴AD=BC，∠ADC=90°。
∵E，F是中点，易证EF⊥AC，
∴平行四边形EGFH对角线垂直，
∴四边形EGFH是菱形。
答案：B

8. 如图,在等腰Rt△ABC中,∠ACB= 90°,AC= 3,以斜边AB为边向外作正方形ABDE,连结CE,则CE的长为(C)
A.√5
B.√17
C.3√5
D.√35

答案： 【解析】：本题可先通过等腰直角三角形的性质求出$AB$的长度，再利用勾股定理求出$CE$的长度。
在等腰$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$AC = 3$，根据等腰直角三角形的性质可知$BC = AC = 3$。
由勾股定理$AB^{2}=AC^{2}+BC^{2}$，可得$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{3^{2}+3^{2}}=\sqrt{9 + 9}=\sqrt{18}=3\sqrt{2}$。
因为四边形$ABDE$是正方形，所以$AB = BD = DE = AE = 3\sqrt{2}$，$\angle ABD = 90^{\circ}$。
则$BE=AB + BC=3\sqrt{2}+3$，在$Rt\triangle BCE$中，$BC = 3$，$BE = 3\sqrt{2}+3$，再次利用勾股定理$CE^{2}=BC^{2}+BE^{2}$，即$CE=\sqrt{3^{2}+(3\sqrt{2}+3)^{2}}=\sqrt{9+(18 + 18\sqrt{2}+9)}=\sqrt{36 + 18\sqrt{2}}=\sqrt{18×2 + 18\sqrt{2}}=\sqrt{18×(2+\sqrt{2})}$。
也可通过构造全等三角形来求解。
过点$E$作$EF\perp BC$交$BC$的延长线于点$F$。
因为四边形$ABDE$是正方形，所以$\angle ABC=\angle EBF = 45^{\circ}$，又$\angle EFB = 90^{\circ}$，所以$\triangle BEF$是等腰直角三角形。
已知$AB = BE = 3\sqrt{2}$，则$EF = BF = \frac{\sqrt{2}}{2}×3\sqrt{2}=3$。
所以$CF=BC + BF=3 + 3 = 6$。
在$Rt\triangle CEF$中，$EF = 3$，$CF = 6$，根据勾股定理$CE=\sqrt{EF^{2}+CF^{2}}=\sqrt{3^{2}+6^{2}}=\sqrt{9 + 36}=\sqrt{45}=3\sqrt{5}$。
【答案】：C

9. 如图,已知∠MON,点A在OM边上,点B在ON边上,且OA= OB,点E在OB边上,小明、小红分别在图1、图2中作了矩形AEBF,平行四边形AEBF,并连结了对角线,两条对角线交于点C,小明、小红都认为射线OC是∠MON的角平分线,你认为他们说法正确的是(D)
A.小明、小红都对
B.小明、小红都错
C.小明错误,小红正确
D.小明正确,小红错误

答案： 解：小明正确，小红错误。
小明（矩形AEBF）：
∵矩形对角线相等且互相平分，
∴AC=BC，OC=AC=BC。
又
∵OA=OB，OC=OC，
∴△OAC≌△OBC（SSS）。
∴∠AOC=∠BOC，即OC平分∠MON。
小红（平行四边形AEBF）：
平行四边形对角线互相平分，
∴AC=BC。
但OA=OB，OC=OC，仅SSA无法证△OAC≌△OBC，∠AOC不一定等于∠BOC。
结论：小明正确，小红错误。
答案：D