2025年本土假期作业巩固训练八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年本土假期作业巩固训练八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第55页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
专题 3 方差
知识清单
1. 方差用来衡量一组数据的离散程度(即这组数据偏离
2. 方差:样本 $ x_1,x_2,x_3,x_4,\cdots,x_n $ 的平均数是 $ \overline{x} $,则样本的方差为
3. 方差越大,数据的波动
知识清单
1. 方差用来衡量一组数据的离散程度(即这组数据偏离
平均数
的大小)。2. 方差:样本 $ x_1,x_2,x_3,x_4,\cdots,x_n $ 的平均数是 $ \overline{x} $,则样本的方差为
$s^2 = \frac{1}{n}[(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \ldots + (x_n - \overline{x})^2]$
。3. 方差越大,数据的波动
越大
,数据越不稳定
;方差越小,数据的波动越小
,数据越稳定
。
答案:
【解析】:
本题主要考查了方差的概念、计算以及方差与数据波动的关系。
1. 方差是用来衡量一组数据偏离其平均数的大小,即数据的离散程度。
2. 方差的计算公式是基于每个数据与平均数的差的平方的平均值。对于样本$x_1, x_2, x_3, \ldots, x_n$,其平均数为$\overline{x}$,则方差$s^2$的计算公式为:
$s^2 = \frac{1}{n}[(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \ldots + (x_n - \overline{x})^2]$
3. 方差与数据的波动有直接关系。方差越大,说明数据偏离平均数的程度越大,即数据的波动越大,数据越不稳定;反之,方差越小,数据的波动越小,数据越稳定。
【答案】:
1. 平均数
2. $s^2 = \frac{1}{n}[(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \ldots + (x_n - \overline{x})^2]$
3. 越大;不稳定;越小;稳定
本题主要考查了方差的概念、计算以及方差与数据波动的关系。
1. 方差是用来衡量一组数据偏离其平均数的大小,即数据的离散程度。
2. 方差的计算公式是基于每个数据与平均数的差的平方的平均值。对于样本$x_1, x_2, x_3, \ldots, x_n$,其平均数为$\overline{x}$,则方差$s^2$的计算公式为:
$s^2 = \frac{1}{n}[(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \ldots + (x_n - \overline{x})^2]$
3. 方差与数据的波动有直接关系。方差越大,说明数据偏离平均数的程度越大,即数据的波动越大,数据越不稳定;反之,方差越小,数据的波动越小,数据越稳定。
【答案】:
1. 平均数
2. $s^2 = \frac{1}{n}[(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + \ldots + (x_n - \overline{x})^2]$
3. 越大;不稳定;越小;稳定
例 1 如果一组数据 6,7,$ x $,9,5 的平均数是 $ 2x $,那么这组数据的方差为()
A.4
B.3
C.2
D.1
A.4
B.3
C.2
D.1
答案:
【解析】:
首先,根据平均数的定义,我们有:
$\frac{6 + 7 + x + 9 + 5}{5} = 2x$
解这个方程,我们得到:
$6 + 7 + x + 9 + 5 = 10x$
$27 + x = 10x$
$9x = 27$
$x = 3$
得到 $x = 3$ 后,我们可以计算这组数据的方差。
方差 $s^2$ 的定义为:
$s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$
其中 $n$ 是数据的数量,$x_i$ 是每一个数据,$\bar{x}$ 是平均数。
将 $x = 3$ 代入原数据,得到数据组为 $6, 7, 3, 9, 5$,其平均数为 $2 × 3 = 6$。
计算方差:
$s^2 = \frac{1}{5} \left[ (6 - 6)^2 + (7 - 6)^2 + (3 - 6)^2 + (9 - 6)^2 + (5 - 6)^2 \right]$
$s^2 = \frac{1}{5} \left[ 0 + 1 + 9 + 9 + 1 \right]$
$s^2 = \frac{1}{5} × 20$
$s^2 = 4$
【答案】:
A. $4$
首先,根据平均数的定义,我们有:
$\frac{6 + 7 + x + 9 + 5}{5} = 2x$
解这个方程,我们得到:
$6 + 7 + x + 9 + 5 = 10x$
$27 + x = 10x$
$9x = 27$
$x = 3$
得到 $x = 3$ 后,我们可以计算这组数据的方差。
方差 $s^2$ 的定义为:
$s^2 = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2$
其中 $n$ 是数据的数量,$x_i$ 是每一个数据,$\bar{x}$ 是平均数。
将 $x = 3$ 代入原数据,得到数据组为 $6, 7, 3, 9, 5$,其平均数为 $2 × 3 = 6$。
计算方差:
$s^2 = \frac{1}{5} \left[ (6 - 6)^2 + (7 - 6)^2 + (3 - 6)^2 + (9 - 6)^2 + (5 - 6)^2 \right]$
$s^2 = \frac{1}{5} \left[ 0 + 1 + 9 + 9 + 1 \right]$
$s^2 = \frac{1}{5} × 20$
$s^2 = 4$
【答案】:
A. $4$
例 2 甲、乙两人进行飞镖比赛,每人投 5 次,所得平均环数相等,其中甲所得环数的方差为 5,乙所得环数如下:2,3,5,7,8,那么成绩较稳定的是________。(选填“甲”或“乙”)
答案:
【解析】:
本题考查了方差的定义和性质。方差是衡量数据波动大小的一个指标,方差越小,表示数据越稳定,波动越小。
首先,我们需要计算乙所得环数的方差。
乙的平均环数为:
$\overset{―}{x} = \frac{1}{5}(2 + 3 + 5 + 7 + 8) = 5$
接下来,我们计算乙的方差 $s^{2}$:
$s^{2} = \frac{1}{5}\lbrack(2 - 5)^{2} + (3 - 5)^{2} + (5 - 5)^{2} + (7 - 5)^{2} + (8 - 5)^{2}\rbrack$
$= \frac{1}{5}×(9 + 4 + 0 + 4 + 9)$
$= \frac{1}{5} × 26$
$= 5.2$
已知甲的方差为5,比较甲、乙两人的方差,我们有 $s_{甲}^{2} = 5 < s_{乙}^{2} = 5.2$。
由于方差越小,数据越稳定,所以甲的成绩更稳定。
【答案】:甲
本题考查了方差的定义和性质。方差是衡量数据波动大小的一个指标,方差越小,表示数据越稳定,波动越小。
首先,我们需要计算乙所得环数的方差。
乙的平均环数为:
$\overset{―}{x} = \frac{1}{5}(2 + 3 + 5 + 7 + 8) = 5$
接下来,我们计算乙的方差 $s^{2}$:
$s^{2} = \frac{1}{5}\lbrack(2 - 5)^{2} + (3 - 5)^{2} + (5 - 5)^{2} + (7 - 5)^{2} + (8 - 5)^{2}\rbrack$
$= \frac{1}{5}×(9 + 4 + 0 + 4 + 9)$
$= \frac{1}{5} × 26$
$= 5.2$
已知甲的方差为5,比较甲、乙两人的方差,我们有 $s_{甲}^{2} = 5 < s_{乙}^{2} = 5.2$。
由于方差越小,数据越稳定,所以甲的成绩更稳定。
【答案】:甲
例 3 甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
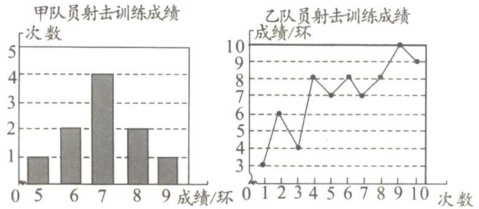
根据以上信息,整理分析数据如下:
| |平均成绩/环|中位数/环|众数/环|方差/环|
|----|----|----|----|----|
|甲|$ a $|7|7|1.2|
|乙|7|$ b $|8|$ c $|
(1)写出表格中 $ a,b,c $ 的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩。若选派其中一名参赛,你认为应选哪名队员?

根据以上信息,整理分析数据如下:
| |平均成绩/环|中位数/环|众数/环|方差/环|
|----|----|----|----|----|
|甲|$ a $|7|7|1.2|
|乙|7|$ b $|8|$ c $|
(1)写出表格中 $ a,b,c $ 的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩。若选派其中一名参赛,你认为应选哪名队员?
答案:
【解析】:(1)本题考查利用平均数的计算公式计算平均成绩,利用中位数的定义求中位数,利用方差公式计算方差。
甲的平均成绩计算:
根据平均数的定义,平均成绩是所有成绩之和除以成绩的数量。
甲的成绩分布为:5环1次,6环2次,7环4次,8环2次,9环1次。
因此,甲的平均成绩 $a = \frac{(5 × 1 + 6 × 2 + 7 × 4 + 8 × 2 + 9 × 1)}{(1 + 2 + 4 + 2 + 1)} = 7$(环)。
乙的中位数计算:
将乙的成绩从小到大排列:3,4,6,7,7,8,8,8,9,10。
由于成绩数量是偶数,中位数是中间两个数的平均值,即 $b = \frac{(7 + 8)}{2} = 7.5$(环)。
乙的方差计算:
方差是每个数据与平均数的差的平方的平均值。
乙的平均成绩也是7环。
因此,乙的方差 $c = \frac{1}{10} × [(3 - 7)^{2} + (4 - 7)^{2} + (6 - 7)^{2} + 2 × (7 - 7)^{2} + 3 × (8 - 7)^{2} + (9 - 7)^{2} + (10 - 7)^{2}] = \frac{1}{10} × (16 + 9 + 1 + 3 + 4 + 9)= 4.2$。
(2)本题考查平均数、中位数、众数和方差在数据分析中的应用。
平均数分析:
甲和乙的平均成绩都是7环,说明两人的总体水平相当。
中位数分析:
甲的中位数是7环,乙的中位数是7.5环。
这意味着乙在射击中更频繁地获得高于7环的成绩。
众数分析:
甲的众数是7环,乙的众数是8环。
这表明甲更常射中7环,而乙更常射中8环。
方差分析:
甲的方差较小(1.2),说明甲的成绩更稳定,波动较小;乙的方差较大(4.2),说明乙的成绩波动较大,但获得高分的可能性也更大。
综合以上分析,虽然甲的成绩更稳定,但乙获得高分的可能性更大。
因此,如果目标是选派一名可能获得更高分的队员,应选择乙。
【答案】:
(1)$a=7$,$b=7.5$,$c=4.2$。
(2)乙。
甲的平均成绩计算:
根据平均数的定义,平均成绩是所有成绩之和除以成绩的数量。
甲的成绩分布为:5环1次,6环2次,7环4次,8环2次,9环1次。
因此,甲的平均成绩 $a = \frac{(5 × 1 + 6 × 2 + 7 × 4 + 8 × 2 + 9 × 1)}{(1 + 2 + 4 + 2 + 1)} = 7$(环)。
乙的中位数计算:
将乙的成绩从小到大排列:3,4,6,7,7,8,8,8,9,10。
由于成绩数量是偶数,中位数是中间两个数的平均值,即 $b = \frac{(7 + 8)}{2} = 7.5$(环)。
乙的方差计算:
方差是每个数据与平均数的差的平方的平均值。
乙的平均成绩也是7环。
因此,乙的方差 $c = \frac{1}{10} × [(3 - 7)^{2} + (4 - 7)^{2} + (6 - 7)^{2} + 2 × (7 - 7)^{2} + 3 × (8 - 7)^{2} + (9 - 7)^{2} + (10 - 7)^{2}] = \frac{1}{10} × (16 + 9 + 1 + 3 + 4 + 9)= 4.2$。
(2)本题考查平均数、中位数、众数和方差在数据分析中的应用。
平均数分析:
甲和乙的平均成绩都是7环,说明两人的总体水平相当。
中位数分析:
甲的中位数是7环,乙的中位数是7.5环。
这意味着乙在射击中更频繁地获得高于7环的成绩。
众数分析:
甲的众数是7环,乙的众数是8环。
这表明甲更常射中7环,而乙更常射中8环。
方差分析:
甲的方差较小(1.2),说明甲的成绩更稳定,波动较小;乙的方差较大(4.2),说明乙的成绩波动较大,但获得高分的可能性也更大。
综合以上分析,虽然甲的成绩更稳定,但乙获得高分的可能性更大。
因此,如果目标是选派一名可能获得更高分的队员,应选择乙。
【答案】:
(1)$a=7$,$b=7.5$,$c=4.2$。
(2)乙。
1. 某地统计最近五年报名参加中考人数增长率分别为:3.9%,4.3%,3.7%,4.3%,4.7%,业内人士评论说:“这五年中考人数增长率相当平稳”,从统计角度看,“增长率相当平稳”说明这组数据________比较小(
A.方差
B.平均数
C.众数
D.中位数
A
)A.方差
B.平均数
C.众数
D.中位数
答案:
【解析】:
本题考察的是对统计数据的理解以及方差、平均数、众数、中位数概念的应用。题目中提到了“增长率相当平稳”,这通常意味着数据之间的波动较小。在统计学中,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
平均数表示一组数据的平均水平;众数是一组数据中出现次数最多的数值;中位数是将一组数据从小到大排序后,位于中间位置的数值。这三个统计量都不能直接反映数据的波动情况。
因此,从统计角度看,“增长率相当平稳”说明这组数据的方差比较小。
【答案】:
A.方差
本题考察的是对统计数据的理解以及方差、平均数、众数、中位数概念的应用。题目中提到了“增长率相当平稳”,这通常意味着数据之间的波动较小。在统计学中,方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
平均数表示一组数据的平均水平;众数是一组数据中出现次数最多的数值;中位数是将一组数据从小到大排序后,位于中间位置的数值。这三个统计量都不能直接反映数据的波动情况。
因此,从统计角度看,“增长率相当平稳”说明这组数据的方差比较小。
【答案】:
A.方差
2. 某校举行健美操比赛,甲、乙两个班各选 10 名学生参加比赛,两个班参赛学生的平均身高都是 1.65 米,其方差分别是 $ s_{甲}^2 = 1.9 $,$ s_{乙}^2 = 2.4 $,则参赛学生身高比较整齐的班级是(
A.甲班
B.乙班
C.同样整齐
D.无法确定
A
)A.甲班
B.乙班
C.同样整齐
D.无法确定
答案:
【解析】:
本题考查方差的意义。方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
题目中给出了甲、乙两个班级学生的身高方差,分别是 $s_{甲}^2 = 1.9$ 和 $s_{乙}^2 = 2.4$。
根据方差的意义,我们可以判断,由于 $s_{甲}^2 < s_{乙}^2$,甲班的学生身高数据波动较小,因此甲班的学生身高更加整齐。
【答案】:
A.甲班
本题考查方差的意义。方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定。
题目中给出了甲、乙两个班级学生的身高方差,分别是 $s_{甲}^2 = 1.9$ 和 $s_{乙}^2 = 2.4$。
根据方差的意义,我们可以判断,由于 $s_{甲}^2 < s_{乙}^2$,甲班的学生身高数据波动较小,因此甲班的学生身高更加整齐。
【答案】:
A.甲班
查看更多完整答案,请扫码查看


