《2025年本土假期作业巩固训练八年级数学》

专题 6 正方形的判定
知识清单
正方形的判定
(1)有一个角是直角的菱形是正方形;
(2)对角线相等的菱形是正方形;
(3)一组邻边相等的矩形是正方形;
(4)对角线互相垂直的矩形是正方形.

答案： 【解析】：
本题考查正方形的判定方法，涉及到菱形和矩形的性质。
正方形的定义是四条边相等且每个角都是直角的四边形。
因此，我们需要找出哪些条件的菱形或矩形可以满足正方形的定义。
对于菱形，由于它本身四边相等，所以只需要满足每个角都是直角或者对角线相等，就可以判定为正方形。
对于矩形，由于它本身每个角都是直角，所以只需要满足一组邻边相等或者对角线互相垂直，就可以判定为正方形。
【答案】：
(1)有一个角是直角的菱形是正方形；
(2)对角线相等的菱形是正方形；
(3)一组邻边相等的矩形是正方形；
(4)对角线互相垂直的矩形是正方形。

例 1 一个四边形顺次添加下列条件中的三个条件便得到正方形:
a. 两组对边分别相等
b. 一组对边平行且相等
c. 一组邻边相等
d. 一个角是直角
顺次添加的条件:①a→c→d;②b→d→c;③a→b→c.
则正确的是 (C)

A.仅①
B.仅③
C.①②
D.②③

答案： 【解析】：
首先，我们分析每一组条件：
①$a\rightarrow c\rightarrow d$：
条件$a$：两组对边分别相等，得到四边形是平行四边形。
条件$c$：一组邻边相等，在平行四边形的基础上，得到平行四边形是菱形。
条件$d$：一个角是直角，在菱形的基础上，得到菱形是正方形。
所以，选项①是正确的。
②$b\rightarrow d\rightarrow c$：
条件$b$：一组对边平行且相等，得到四边形是平行四边形。
条件$d$：一个角是直角，在平行四边形的基础上，得到平行四边形是矩形。
条件$c$：一组邻边相等，在矩形的基础上，得到矩形是正方形。
所以，选项②是正确的。
③$a\rightarrow b\rightarrow c$：
条件$a$和$b$都得到四边形是平行四边形，但添加条件$c$只能得到平行四边形是菱形，并不能得到正方形。
所以，选项③是不正确的。
综上所述，只有选项①和②是正确的。
【答案】：C

例 2 如图,在矩形 ABCD 中,对角线 AC,BD 相交于点 O,在不添加任何辅助线的情况下,请你添加一个条件____,使矩形 ABCD 是正方形.

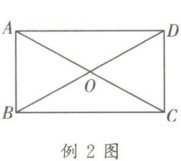
答案： 【解析】：
四边形$ABCD$是矩形，根据矩形的性质，其对角线相等，即$AC=BD$，且对边相等，即$AB=CD$，$AD=BC$。
为了使矩形$ABCD$成为正方形，需要满足正方形的定义，即所有边相等且每个角都是直角。
由于矩形已经满足了每个角都是直角的条件，只需要再满足所有边相等即可。
观察矩形$ABCD$，可以发现如果$AB=AD$，那么由于$AB=CD$和$AD=BC$，就可以推出$AB=BC=CD=AD$，从而满足正方形的定义。
另一种方法是利用正方形的对角线性质，即正方形的对角线互相垂直。
因此，如果$AC\perp BD$，结合矩形的对角线相等且平分的性质，也可以推出矩形$ABCD$是正方形。
【答案】：
$AB = AD$（或 $AC\perp BD$ 答案不唯一）。

例 3 如图,在等腰直角△ABC 中,∠BAC= 90°,D,E 是 BC 上的两点,且 BD= CE,过 D,E 作 DM,EN 分别垂直 AB,AC,垂足为 M,N,延长 MD,NE,交于点 F,连结 AD,AE.其中:①四边形 AMFN 是正方形;②△ABE≌△ACD;③当∠DAE= 45°时$,CE^2 + BD^2= DE^2.$正确的结论有____(填序号).

答案： 解：①
∵△ABC是等腰直角三角形，∠BAC=90°，
∴∠B=∠C=45°，AB=AC.
∵DM⊥AB，EN⊥AC，∠BAC=90°，
∴∠FMA=∠FNA=∠BAC=90°，
∴四边形AMFN是矩形.
∵∠B=45°，DM⊥AB，
∴△BDM是等腰直角三角形，BM=DM.
同理，CN=EN.
∵BD=CE，
∴BM=CN.
∵AB=AC，
∴AB-BM=AC-CN，即AM=AN.
∵四边形AMFN是矩形且AM=AN，
∴四边形AMFN是正方形.
②
∵AB=AC，∠B=∠C，BD=CE，
∴BE=BC-CE，CD=BC-BD，
∵BD=CE，
∴BE=CD.
在△ABE和△ACD中，
AB=AC，∠B=∠C，BE=CD，
∴△ABE≌△ACD(SAS).
③
将△ACE绕点A顺时针旋转90°，得到△ABD'，
则AD'=AE，BD'=CE，∠BAD'=∠CAE，∠ABD'=∠C=45°.
∵∠DAE=45°，∠BAC=90°，
∴∠BAD+∠CAE=45°，
∴∠BAD+∠BAD'=45°，即∠DAD'=45°.
在△DAD'和△DAE中，
AD=AD，∠DAD'=∠DAE，AD'=AE，
∴△DAD'≌△DAE(SAS)，
∴D'D=DE.
∵∠ABD'=45°，∠ABC=45°，
∴∠DBD'=90°.
在Rt△DBD'中，BD²+BD'²=D'D²，
∵BD'=CE，D'D=DE，
∴BD²+CE²=DE².
正确的结论有①②③.
答案：①②③

例 4 如图所示,在正方形 ABCD 中,DF= AP= BQ= CE.
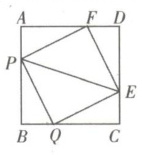
(1)试判断四边形 PQEF 是否是正方形,并证明;
(2)PE 是否总过某一定点,并说明理由.

答案：

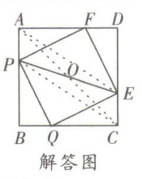
(1)四边形 PQEF 是正方形，证明如下：
∵四边形 ABCD 是正方形，
∴AB=BC=CD=DA，∠BAD=∠B=∠BCD=∠D=90°，
∵DF=AP=BQ=CE，
∴BP=QC=ED=FA，
在△AFP、△BPQ、△CQE、△DEF 中，
$\left\{\begin{array}{l}AF=BP=CQ=DE\\ \angle FAP=\angle PBQ=\angle QCE=\angle EDF\\ AP=BQ=CE=DF\end{array}\right.$，
∴△AFP≌△BPQ≌△CQE≌△DEF(SAS)，
∴FP=PQ=QE=EF，∠APF=∠PQB，
∴四边形 PQEF 是菱形，
∵∠PQB + ∠BPQ=90°，
∴∠APF + ∠BPQ=90°，
∴∠FPQ=180° - (∠APF + ∠BPQ)=90°，
∴四边形 PQEF 是正方形；
(2)PE 总过 AC 的中点，理由如下：
连结 AC，交 PE 于点 O，连结 AE、PC，
∵AP=CE，且 AP//CE，
∴四边形 APCE 是平行四边形，
∵平行四边形对角线互相平分，
∴O 为 AC 的中点，即 PE 总过 AC 的中点。