《2025年本土假期作业巩固训练八年级数学》

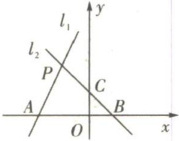
19. 如图,过点$A(-2,0)的直线l_{1}:y = kx + b与直线l_{2}:y = -x + 1交于P(-1,a)$。
(1)求直线$l_{1}$对应的表达式；
(2)直接写出方程组$\begin{cases}y = kx + b,\\y = -x + 1\end{cases} $的解。
(3)求四边形$PAOC$的面积。

答案：
(1)解：因为点$P(-1,a)$在直线$l_{2}:y=-x + 1$上，所以将$x=-1$代入$y=-x + 1$，得$a=-(-1)+1=2$，即$P(-1,2)$。
因为直线$l_{1}:y=kx + b$过点$A(-2,0)$和$P(-1,2)$，所以可得方程组$\begin{cases}-2k + b=0\\-k + b=2\end{cases}$，用第二个方程减去第一个方程得：$(-k + b)-(-2k + b)=2 - 0$，即$k=2$，将$k=2$代入$-2k + b=0$，得$-4 + b=0$，解得$b=4$，所以直线$l_{1}$的表达式为$y=2x + 4$。
(2)$\begin{cases}x=-1\\y=2\end{cases}$
(3)解：对于直线$l_{2}:y=-x + 1$，令$x=0$，得$y=1$，所以$C(0,1)$；对于直线$l_{1}:y=2x + 4$，令$x=0$，得$y=4$，设直线$l_{1}$与$y$轴交于点$D$，则$D(0,4)$。
$S_{\triangle AOD}=\frac{1}{2}× OA× OD=\frac{1}{2}×2×4 = 4$，$S_{\triangle PCD}=\frac{1}{2}× CD×|x_{P}|=\frac{1}{2}×(4 - 1)×1=\frac{3}{2}$，所以$S_{四边形 PAOC}=S_{\triangle AOD}-S_{\triangle PCD}=4-\frac{3}{2}=\frac{5}{2}$。

20. 设一次函数$y = a(x - 2) + 1$($a$是常数,$a \neq 0$)。
(1)若点$(4,3)$在该一次函数图象上,求$a$的值。
(2)当$2 \leq x \leq 3$时,该函数的最大值是 3,求$a$的值。
(3)若点$A(m,n)和点B(m + 1,n + 3)$都在该一次函数图象上,判断反比例函数$y = \frac{a}{x}$的图象所在象限。

答案： 【解析】：
本题主要考察一次函数的定义、性质以及反比例函数图象与系数的关系。
(1)将点$(4,3)$代入函数$y = a(x - 2) + 1$，即可求出$a$的值。
(2)对于$2 \leq x \leq 3$，需要分$a \gt 0$和$a \lt 0$两种情况讨论，根据一次函数的单调性确定最大值，从而求出$a$的值。
(3)将点$A(m,n)$和点$B(m + 1,n + 3)$代入函数$y = a(x - 2) + 1$，得到两个方程，解出$a$的值，再根据$a$的正负判断反比例函数$y = \frac{a}{x}$的图象所在象限。
【答案】：
(1)
解：将点$(4,3)$代入$y = a(x - 2) + 1$，得：
$3 = a(4 - 2) + 1$，
$3 = 2a + 1$，
$2a = 2$，
$a = 1$。
(2)
当$a \gt 0$时，函数$y = a(x - 2) + 1$为增函数，
所以当$x = 3$时，$y$取最大值3，
即$3 = a(3 - 2) + 1$，
$3 = a + 1$，
$a = 2$；
当$a \lt 0$时，函数$y = a(x - 2) + 1$为减函数，
所以当$x = 2$时，$y$取最大值3，
即$3 = a(2 - 2) + 1$，
$3 = 1$（无解），
综上，$a = 2$。
(3)
将点$A(m,n)$代入$y = a(x - 2) + 1$，得：
$n = a(m - 2) + 1$，
即$a(m - 2) = n - 1$ ①，
将点$B(m + 1,n + 3)$代入$y = a(x - 2) + 1$，得：
$n + 3 = a(m + 1 - 2) + 1$，
即$a(m - 1) = n + 2$ ②，
②-①得：
$a = 3$，
因为$a = 3 \gt 0$，
所以反比例函数$y = \frac{a}{x}$的图象在第一、三象限。

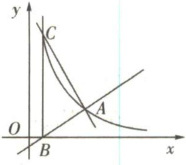
21. 如图,一次函数$y_{1} = \frac{2}{3}x + b与反比例函数y_{2} = \frac{k}{x}(x ＞ 0)的图象交于点A(4,2)$,与$x轴交于点B$。
(1)填空：$k = $______8,$b = $______$-\frac{2}{3}$；
(2)过点$B作BC \perp x$轴,交反比例函数的图象于点$C$,试求直线$AC解析式y_{3}$的表达式；
解：对于$y_{1}=\frac{2}{3}x-\frac{2}{3}$，令$y_{1}=0$，则$\frac{2}{3}x-\frac{2}{3}=0$，解得$x=1$，$\therefore B(1,0)$。
$\because BC\perp x$轴，$\therefore$点$C$的横坐标为1。
将$x=1$代入$y_{2}=\frac{8}{x}$，得$y=8$，$\therefore C(1,8)$。
设直线$AC$的解析式为$y_{3}=mx+n$，
将$A(4,2)$，$C(1,8)$代入，得$\left\{\begin{array}{l}4m+n=2\\m+n=8\end{array}\right.$，
解得$\left\{\begin{array}{l}m=-2\\n=10\end{array}\right.$，$\therefore y_{3}=-2x+10$。
(3)观察图象,直接写出当$x ＞ 0$时,不等式组$\frac{2}{3}x + b ＜ \frac{k}{x} ＜ y_{3}$的解集。$1\lt x\lt4$

答案：
(1)8；$-\frac{2}{3}$
(2)解：对于$y_{1}=\frac{2}{3}x-\frac{2}{3}$，令$y_{1}=0$，则$\frac{2}{3}x-\frac{2}{3}=0$，解得$x=1$，$\therefore B(1,0)$。
$\because BC\perp x$轴，$\therefore$点$C$的横坐标为1。
将$x=1$代入$y_{2}=\frac{8}{x}$，得$y=8$，$\therefore C(1,8)$。
设直线$AC$的解析式为$y_{3}=mx+n$，
将$A(4,2)$，$C(1,8)$代入，得$\left\{\begin{array}{l}4m+n=2\\m+n=8\end{array}\right.$，
解得$\left\{\begin{array}{l}m=-2\\n=10\end{array}\right.$，$\therefore y_{3}=-2x+10$。
(3)$1\lt x\lt4$

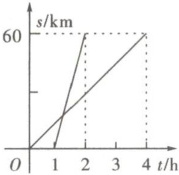
22. $A$,$B$两地相距 60 km,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由$A到达B$地,他们行进中的路程$s(km)与甲出发后的时间t(h)$之间的函数图象如图所示。
(1)乙比甲晚出发几小时？比甲早到几小时？
(2)分别写出甲走的路程$s_{1}(km)$,乙走的路程$s_{2}(km)与时间t(h)$之间的函数关系式；
(3)乙在出发后几小时追上了甲,追上甲的地点离$A$地多远？

答案： 【解析】：本题主要考查了函数图象的应用以及一次函数关系式的求解和追及问题的计算。
（1）从图象中可以直接看出甲出发$1$小时后乙才出发，所以乙比甲晚出发$1$小时；
甲$4$小时到达$B$地，乙$3 - 1 = 2$小时到达$B$地，所以乙比甲早到$4 - 3 = 1$小时。
（2）对于甲：
甲是匀速行驶，路程$s_1$与时间$t$成正比例关系，设$s_1 = k_1t$（$k_1\neq0$）。
已知甲$4$小时行驶$60km$，即当$t = 4$时，$s_1 = 60$，代入$s_1 = k_1t$可得：
$60 = 4k_1$，
解得$k_1 = 15$，
所以甲走的路程$s_1(km)$与时间$t(h)$之间的函数关系式为$s_1 = 15t(0\leq t\leq4)$。
对于乙：
乙的运动过程分为两段，当$0\leq t\leq1$时，$s_2 = 0$；
当$1\lt t\leq3$时，设$s_2 = k_2t + b$（$k_2\neq0$），
因为图象过点$(1,0)$和$(3,60)$，将这两点代入$s_2 = k_2t + b$可得方程组：
$\begin{cases}k_2 + b = 0,\\3k_2 + b = 60.\end{cases}$
用第二个方程减去第一个方程消去$b$可得：
$3k_2 + b - (k_2 + b) = 60 - 0$，
$3k_2 + b - k_2 - b = 60$，
$2k_2 = 60$，
解得$k_2 = 30$，
将$k_2 = 30$代入$k_2 + b = 0$可得：
$30 + b = 0$，
解得$b = - 30$，
所以当$1\lt t\leq3$时，$s_2 = 30t - 30$，
综上，乙走的路程$s_2(km)$与时间$t(h)$之间的函数关系式为$s_2=\begin{cases}0(0\leq t\leq1),\\30t - 30(1\lt t\leq3).\end{cases}$
（3）设乙出发后$x$小时追上甲。
甲的速度为$60÷4 = 15(km/h)$，甲出发$(x + 1)$小时的路程为$15(x + 1)km$；
乙的速度为$60÷(3 - 1)= 30(km/h)$，乙出发$x$小时的路程为$30xkm$。
当乙追上甲时，两人行驶的路程相等，则可列方程：
$15(x + 1) = 30x$，
$15x + 15 = 30x$，
$30x - 15x = 15$，
$15x = 15$，
解得$x = 1$。
此时乙行驶的路程$s_2 = 30×1 = 30(km)$，即追上甲的地点离$A$地$30km$。
【答案】：
(1)乙比甲晚出发$1$小时，比甲早到$1$小时；
(2)$s_1 = 15t(0\leq t\leq4)$，$s_2=\begin{cases}0(0\leq t\leq1),\\30t - 30(1\lt t\leq3);\end{cases}$
(3)乙在出发后$1$小时追上了甲，追上甲的地点离$A$地$30km$。