2025年本土假期作业巩固训练八年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年本土假期作业巩固训练八年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
23. 如图,已知四边形ABCD是长方形,点E在BA的延长线上,AE= AD,EC与BD相交于点G,与AD相交于点F,AF= AB。
(1)求证:BD⊥EC;
(2)连结AG,求证:EG-DG= √2 AG。

(1)求证:BD⊥EC;
(2)连结AG,求证:EG-DG= √2 AG。

答案:
(1)证明:设AB=AF=a,
∵四边形ABCD是长方形,
∴AB=CD=a,AD=BC,∠EAF=∠DAB=90°,
∵AE=AD,设AE=AD=BC=b,
在△EAF和△DAB中,
$\left\{\begin{array}{l} AE=AD \\ ∠EAF=∠DAB \\ AF=AB \end{array}\right.$,
∴△EAF≌△DAB(SAS),
∴∠E=∠ADB,
∵∠E+∠EFA=90°,∠EFA=∠DFG,
∴∠ADB+∠DFG=90°,
∴∠DGF=90°,即BD⊥EC。
(2)证明:在EG上截取EH=DG,连接AH,
由
(1)知△EAF≌△DAB,
∴∠E=∠ADB,AE=AD,
在△AEH和△ADG中,
$\left\{\begin{array}{l} AE=AD \\ ∠E=∠ADG \\ EH=DG \end{array}\right.$,
∴△AEH≌△ADG(SAS),
∴AH=AG,∠EAH=∠DAG,
∵∠DAG+∠GAE=90°,
∴∠EAH+∠GAE=90°,即∠HAG=90°,
∴△AHG是等腰直角三角形,
∴HG=$\sqrt{2}$AG,
∵EG-EH=HG,EH=DG,
∴EG-DG=$\sqrt{2}$AG。
(1)证明:设AB=AF=a,
∵四边形ABCD是长方形,
∴AB=CD=a,AD=BC,∠EAF=∠DAB=90°,
∵AE=AD,设AE=AD=BC=b,
在△EAF和△DAB中,
$\left\{\begin{array}{l} AE=AD \\ ∠EAF=∠DAB \\ AF=AB \end{array}\right.$,
∴△EAF≌△DAB(SAS),
∴∠E=∠ADB,
∵∠E+∠EFA=90°,∠EFA=∠DFG,
∴∠ADB+∠DFG=90°,
∴∠DGF=90°,即BD⊥EC。
(2)证明:在EG上截取EH=DG,连接AH,
由
(1)知△EAF≌△DAB,
∴∠E=∠ADB,AE=AD,
在△AEH和△ADG中,
$\left\{\begin{array}{l} AE=AD \\ ∠E=∠ADG \\ EH=DG \end{array}\right.$,
∴△AEH≌△ADG(SAS),
∴AH=AG,∠EAH=∠DAG,
∵∠DAG+∠GAE=90°,
∴∠EAH+∠GAE=90°,即∠HAG=90°,
∴△AHG是等腰直角三角形,
∴HG=$\sqrt{2}$AG,
∵EG-EH=HG,EH=DG,
∴EG-DG=$\sqrt{2}$AG。
24. 如图,在□ABCD中,各内角的平分线分别相交于点E,F,G,H。
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB= 6,BC= 4,∠DAB= 60°,求四边形EFGH的面积。
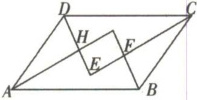
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB= 6,BC= 4,∠DAB= 60°,求四边形EFGH的面积。

答案:
(1)证明:在□ABCD中,AB=CD,∠DAB=∠BCD,∠ABC=∠ADC。
∵AG、CE分别平分∠DAB、∠BCD,
∴∠BAG=∠DAB/2,∠DCE=∠BCD/2,
∴∠BAG=∠DCE。
同理,∠ABG=∠CDE。
在△ABG和△CDE中,
∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,
∴△ABG≌△CDE(ASA)。
(2)四边形EFGH是矩形。
证明:在□ABCD中,AD//BC,
∴∠DAB+∠ABC=180°。
∵AG、BG分别平分∠DAB、∠ABC,
∴∠GAB+∠GBA=(∠DAB+∠ABC)/2=90°,
∴∠AGB=90°。
同理,∠DEC=90°,∠AHD=90°=∠EHG。
∴四边形EFGH有三个直角,故四边形EFGH是矩形。
(3)解:在□ABCD中,AD=BC=4,AB=CD=6,∠DAB=60°。
作GM⊥AB于M,在Rt△AGM中,∠GAM=30°,设GM=x,则AG=2x,AM=√3x。
在Rt△BGM中,∠GBM=60°,BM=GM/tan60°=x/√3,BG=2x/√3。
∵AB=AM+BM=√3x + x/√3=6,解得x= (3√3)/2。
∴AG=2x=3√3,BG=2x/√3=3。
由△ABG≌△CDE,得DE=BG=3,CE=AG=3√3。
∵AD=4,在Rt△ADH中,∠DAH=30°,DH=AD/2=2,AH=AD·cos30°=2√3。
∴EH=AG - AH=3√3 - 2√3=√3,EF=BG - BF=BG - DH=3 - 2=1。
∴S矩形EFGH=EH·EF=√3×1=√3。
答:四边形EFGH的面积为√3。
(1)证明:在□ABCD中,AB=CD,∠DAB=∠BCD,∠ABC=∠ADC。
∵AG、CE分别平分∠DAB、∠BCD,
∴∠BAG=∠DAB/2,∠DCE=∠BCD/2,
∴∠BAG=∠DCE。
同理,∠ABG=∠CDE。
在△ABG和△CDE中,
∠BAG=∠DCE,AB=CD,∠ABG=∠CDE,
∴△ABG≌△CDE(ASA)。
(2)四边形EFGH是矩形。
证明:在□ABCD中,AD//BC,
∴∠DAB+∠ABC=180°。
∵AG、BG分别平分∠DAB、∠ABC,
∴∠GAB+∠GBA=(∠DAB+∠ABC)/2=90°,
∴∠AGB=90°。
同理,∠DEC=90°,∠AHD=90°=∠EHG。
∴四边形EFGH有三个直角,故四边形EFGH是矩形。
(3)解:在□ABCD中,AD=BC=4,AB=CD=6,∠DAB=60°。
作GM⊥AB于M,在Rt△AGM中,∠GAM=30°,设GM=x,则AG=2x,AM=√3x。
在Rt△BGM中,∠GBM=60°,BM=GM/tan60°=x/√3,BG=2x/√3。
∵AB=AM+BM=√3x + x/√3=6,解得x= (3√3)/2。
∴AG=2x=3√3,BG=2x/√3=3。
由△ABG≌△CDE,得DE=BG=3,CE=AG=3√3。
∵AD=4,在Rt△ADH中,∠DAH=30°,DH=AD/2=2,AH=AD·cos30°=2√3。
∴EH=AG - AH=3√3 - 2√3=√3,EF=BG - BF=BG - DH=3 - 2=1。
∴S矩形EFGH=EH·EF=√3×1=√3。
答:四边形EFGH的面积为√3。
25. 如图1,对角线互相垂直的四边形叫做垂美四边形。
(1)概念理解:如图2,在四边形ABCD中,AB= AD,CB= CD,问:四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,AC⊥BD。试证明:$AB^2+CD^2= AD^2+BC^2;$
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE。已知AC= 4,AB= 5,求GE的长。

(1)概念理解:如图2,在四边形ABCD中,AB= AD,CB= CD,问:四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC,BD交于点O,AC⊥BD。试证明:$AB^2+CD^2= AD^2+BC^2;$
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE,BG,GE。已知AC= 4,AB= 5,求GE的长。

答案:
【解析】:
(1)概念理解部分,本题考查了垂直平分线的性质,通过证明三角形全等,得出两条对角线互相垂直,进而判断四边形ABCD是否为垂美四边形。
(2)性质探究部分,本题考查了勾股定理的应用。利用勾股定理,在四个直角三角形中表示出$AB^2$,$CD^2$,$AD^2$,$BC^2$,然后通过等量代换得出结论。
(3)解决问题部分,本题考查了垂美四边形的性质和勾股定理的应用。首先根据给出的条件证明四边形$CGEB$是垂美四边形,然后利用垂美四边形的性质和勾股定理求出$GE$的长。
【答案】:
(1)四边形ABCD是垂美四边形。理由如下:
连接$AC$,$BD$,
∵$AB=AD$,
∴点$A$在线段$BD$的垂直平分线上。
∵$CB=CD$,
∴点$C$在线段$BD$的垂直平分线上。
∴直线$AC$是线段$BD$的垂直平分线,
∴$AC⊥BD$,即四边形$ABCD$是垂美四边形。
(2)
∵$AC⊥BD$,
∴$\angle AOD=\angle AOB=\angle BOC=\angle COD=90^\circ$,
由勾股定理得,$AB^2+CD^2=AO^2+BO^2+CO^2+DO^2$,$AD^2+BC^2=AO^2+DO^2+BO^2+CO^2$,
∴$AB^2+CD^2=AD^2+BC^2$。
(3)连接$CG$,$BE$,
∵$\angle CAG=\angle BAE=90^\circ$,
∴$\angle CAG+\angle BAC=\angle BAE+\angle BAC$,即$\angle GAB=\angle CAE$,
在$\bigtriangleup GAB$和$\bigtriangleup CAE$中,
$\begin{cases}AG=AC,\\\angle GAB=\angle CAE,\\AB=AE.\end{cases}$
∴$\bigtriangleup GAB\cong\bigtriangleup CAE(SAS)$,
∴$\angle ABG=\angle AEC$,
延长$CE$交$BG$于点$O$,交$AB$于点$F$,
设$AB$与$CE$相交于点$F$,
∵$\angle AEC+\angle AFE=90^\circ$,$\angle AFE=\angle BFO$,
∴$\angle ABG+\angle BFO=90^\circ$,
∴$\angle BOC=90^\circ$,即$CE⊥BG$,
∴四边形$CGEB$是垂美四边形,
由
(2)得,$CG^2+BE^2=CB^2+GE^2$,
∵$AC=4$,$AB=5$,
∴$BC=\sqrt{AB^2-AC^2}=3$,$CG^2=AC^2+AG^2=32$,$BE^2=AB^2+AE^2=50$,
∴$GE^2=CG^2+BE^2-CB^2=73$,
∴$GE=\sqrt{73}$。
(1)概念理解部分,本题考查了垂直平分线的性质,通过证明三角形全等,得出两条对角线互相垂直,进而判断四边形ABCD是否为垂美四边形。
(2)性质探究部分,本题考查了勾股定理的应用。利用勾股定理,在四个直角三角形中表示出$AB^2$,$CD^2$,$AD^2$,$BC^2$,然后通过等量代换得出结论。
(3)解决问题部分,本题考查了垂美四边形的性质和勾股定理的应用。首先根据给出的条件证明四边形$CGEB$是垂美四边形,然后利用垂美四边形的性质和勾股定理求出$GE$的长。
【答案】:
(1)四边形ABCD是垂美四边形。理由如下:
连接$AC$,$BD$,
∵$AB=AD$,
∴点$A$在线段$BD$的垂直平分线上。
∵$CB=CD$,
∴点$C$在线段$BD$的垂直平分线上。
∴直线$AC$是线段$BD$的垂直平分线,
∴$AC⊥BD$,即四边形$ABCD$是垂美四边形。
(2)
∵$AC⊥BD$,
∴$\angle AOD=\angle AOB=\angle BOC=\angle COD=90^\circ$,
由勾股定理得,$AB^2+CD^2=AO^2+BO^2+CO^2+DO^2$,$AD^2+BC^2=AO^2+DO^2+BO^2+CO^2$,
∴$AB^2+CD^2=AD^2+BC^2$。
(3)连接$CG$,$BE$,
∵$\angle CAG=\angle BAE=90^\circ$,
∴$\angle CAG+\angle BAC=\angle BAE+\angle BAC$,即$\angle GAB=\angle CAE$,
在$\bigtriangleup GAB$和$\bigtriangleup CAE$中,
$\begin{cases}AG=AC,\\\angle GAB=\angle CAE,\\AB=AE.\end{cases}$
∴$\bigtriangleup GAB\cong\bigtriangleup CAE(SAS)$,
∴$\angle ABG=\angle AEC$,
延长$CE$交$BG$于点$O$,交$AB$于点$F$,
设$AB$与$CE$相交于点$F$,
∵$\angle AEC+\angle AFE=90^\circ$,$\angle AFE=\angle BFO$,
∴$\angle ABG+\angle BFO=90^\circ$,
∴$\angle BOC=90^\circ$,即$CE⊥BG$,
∴四边形$CGEB$是垂美四边形,
由
(2)得,$CG^2+BE^2=CB^2+GE^2$,
∵$AC=4$,$AB=5$,
∴$BC=\sqrt{AB^2-AC^2}=3$,$CG^2=AC^2+AG^2=32$,$BE^2=AB^2+AE^2=50$,
∴$GE^2=CG^2+BE^2-CB^2=73$,
∴$GE=\sqrt{73}$。
查看更多完整答案,请扫码查看


