《2025年开心假期暑假作业武汉出版社六年级数学》

六、开动脑筋。
在$\frac{15}{x}$里,$x$是什么数时,分数值小于 1？$x$是什么数时,分数值大于 1？$x$能不能是 0 呢？

答案： 【解析】：
首先，我们考虑分数值小于1的情况。
对于分数$\frac{15}{x}$，如果其值小于1，那么可以得出不等式：
$\frac{15}{x} \lt 1$
解这个不等式，我们得到：
$x \gt 15$
接着，我们考虑分数值大于1的情况。
对于分数$\frac{15}{x}$，如果其值大于1，那么可以得出不等式：
$\frac{15}{x} \gt 1$
解这个不等式，我们得到：
$x \lt 15$
但由于分数的分母不能为0，所以$x$必须大于0，即：
$0 \lt x \lt 15$
最后，我们考虑$x$能否为0的情况。
在分数中，分母不能为0，因为这将使得分数无意义。所以，$x$不能为0。
【答案】：
当$x$大于15时，分数值小于1；
当$x$大于0且小于15时，分数值大于1；
$x$不能为0。

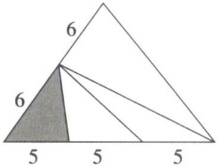
1. 下图阴影部分面积是整个图形面积的几分之几？

答案： 【解析】：观察图形可知，整个图形是一个大三角形，其底边由3段长度均为5的线段组成，所以大三角形的底边长为$5 + 5 + 5=15$，大三角形的左侧腰长为6，右侧腰长也为6，由此可判断这是一个等腰三角形（两腰相等）。
设大三角形的高为$h$，根据三角形面积公式$S=\frac{1}{2}×底×高$，大三角形的面积为$\frac{1}{2}×15× h$。
阴影部分是一个小三角形，它的底边长为5（最左侧的一段底边），且这个小三角形与大三角形共享同一个顶点（顶部顶点），所以它们的高是相同的，均为$h$。那么阴影部分小三角形的面积为$\frac{1}{2}×5× h$。
则阴影部分面积与整个图形面积的比为：$\frac{\frac{1}{2}×5× h}{\frac{1}{2}×15× h}=\frac{5}{15}=\frac{1}{3}$。
【答案】：$\frac{1}{3}$

2. 有一件工程,甲队独做 20 天可以完成它的$\frac{1}{9}$,乙队独做 9 天可以完成它的$\frac{1}{10}$。甲、乙两队合做,需要多少天完成这件工程的一半？

答案： 【解析】：首先，计算甲队的工作效率。甲队独做20天完成工程的$\frac{1}{9}$，则甲队每天完成$\frac{1}{9} ÷ 20 = \frac{1}{180}$。
接着，计算乙队的工作效率。乙队独做9天完成工程的$\frac{1}{10}$，则乙队每天完成$\frac{1}{10} ÷ 9 = \frac{1}{90}$。
然后，求出甲、乙两队合作的工作效率之和：$\frac{1}{180} + \frac{1}{90} = \frac{1}{180} + \frac{2}{180} = \frac{3}{180} = \frac{1}{60}$。
最后，计算完成工程一半所需时间。工程的一半为$\frac{1}{2}$，所需时间为$\frac{1}{2} ÷ \frac{1}{60} = 30$（天）。
【答案】：30