2025年开心假期暑假作业武汉出版社六年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年开心假期暑假作业武汉出版社六年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
一、在横线上填上合适的单位。
水杯高1
一枚邮票的面积是4
小英的腰围是6
数学课本的面积是4.8
小强身高128
一块黑板的面积是4
水杯高1
分米
一枚邮票的面积是4
平方厘米
小英的腰围是6
分米
数学课本的面积是4.8
平方分米
小强身高128
厘米
一块黑板的面积是4
平方米
答案:
【解析】:根据生活常识和对长度、面积单位的认识进行填写。水杯高度通常用分米衡量,1分米比较合适;邮票面积较小,用平方厘米,4平方厘米符合实际;腰围一般用分米作单位,6分米合理;数学课本面积用平方分米,4.8平方分米恰当;身高常用厘米,128厘米符合小学生身高;黑板面积较大,用平方米,4平方米正确。
【答案】:分米;平方厘米;分米;平方分米;厘米;平方米
【答案】:分米;平方厘米;分米;平方分米;厘米;平方米
1. 一个三角形的面积是$48cm^2,$与它等底等高的平行四边形面积是(
96
)$cm^2。$
答案:
【解析】:三角形的面积公式是$\frac{1}{2} × \text{底} × \text{高}$,而平行四边形的面积公式是$\text{底} × \text{高}$。
由于平行四边形与三角形等底等高,所以平行四边形的面积是三角形面积的两倍。
给定三角形的面积是$48cm^2$,所以平行四边形的面积为$48cm^2 × 2 = 96cm^2$。
【答案】:96
由于平行四边形与三角形等底等高,所以平行四边形的面积是三角形面积的两倍。
给定三角形的面积是$48cm^2$,所以平行四边形的面积为$48cm^2 × 2 = 96cm^2$。
【答案】:96
2. 用一根长12.56cm的铁丝围成一个尽可能大的正方形,它的面积是(
9.8596
)cm²;如果围成一个尽可能大的圆,它的面积是(12.56
)cm²。
答案:
【解析】:首先,用铁丝围成正方形时,铁丝的长度就是正方形的周长。正方形的周长=边长×4,所以边长=周长÷4,即12.56÷4=3.14cm。正方形的面积=边长×边长,所以面积为3.14×3.14=9.8596cm²。
其次,用铁丝围成圆时,铁丝的长度就是圆的周长。圆的周长公式为C=2πr,所以半径r=C÷(2π)=12.56÷(2×3.14)=2cm。圆的面积公式为S=πr²,所以面积为3.14×2²=12.56cm²。
【答案】:9.8596;12.56
其次,用铁丝围成圆时,铁丝的长度就是圆的周长。圆的周长公式为C=2πr,所以半径r=C÷(2π)=12.56÷(2×3.14)=2cm。圆的面积公式为S=πr²,所以面积为3.14×2²=12.56cm²。
【答案】:9.8596;12.56
3. 如果大圆半径是小圆半径的2倍,那么大圆直径是小圆直径的(
2
)倍,大圆周长是小圆周长的(2
)倍,大圆面积是小圆面积的(4
)倍。
答案:
【解析】:
设小圆的半径为r,则大圆的半径为2r。
1. 对于直径:
小圆的直径 = 2r
大圆的直径 = 2 × 2r = 4r
所以,大圆直径是小圆直径的倍数 = 4r / 2r = 2倍。
2. 对于周长:
小圆的周长 = 2πr
大圆的周长 = 2π × 2r = 4πr
所以,大圆周长是小圆周长的倍数 = 4πr / 2πr = 2倍。
3. 对于面积:
小圆的面积$ = πr^2$
大圆的面积$ = π × (2r)^2 = 4πr^2$
所以,大圆面积是小圆面积的倍数$ = 4πr^2 / πr^2 = 4$倍。
【答案】:
2;2;4
设小圆的半径为r,则大圆的半径为2r。
1. 对于直径:
小圆的直径 = 2r
大圆的直径 = 2 × 2r = 4r
所以,大圆直径是小圆直径的倍数 = 4r / 2r = 2倍。
2. 对于周长:
小圆的周长 = 2πr
大圆的周长 = 2π × 2r = 4πr
所以,大圆周长是小圆周长的倍数 = 4πr / 2πr = 2倍。
3. 对于面积:
小圆的面积$ = πr^2$
大圆的面积$ = π × (2r)^2 = 4πr^2$
所以,大圆面积是小圆面积的倍数$ = 4πr^2 / πr^2 = 4$倍。
【答案】:
2;2;4
4. 如果一个三角形与一个平行四边形面积相等,底边也相等,那么这条相等的底边上三角形的高和平行四边形的高的比是(
2:1
)。
答案:
【解析】:
三角形的面积公式为:面积 = (底 × 高) ÷ 2,
平行四边形的面积公式为:面积 = 底 × 高,
假设三角形和平行四边形的共同底边为 b,三角形的高为 h1,平行四边形的高为 h2。
根据题目,三角形和平行四边形的面积相等,因此:
(b × h1) ÷ 2 = b × h2
两边同时乘以2得到:
b × h1 = 2 × b × h2
由于底边 b 不为零,可以两边同时除以 b,得到:
h1 = 2 × h2
即 h1/h2 = 2/1
所以,三角形的高与平行四边形的高的比是 2:1。
【答案】:2:1
三角形的面积公式为:面积 = (底 × 高) ÷ 2,
平行四边形的面积公式为:面积 = 底 × 高,
假设三角形和平行四边形的共同底边为 b,三角形的高为 h1,平行四边形的高为 h2。
根据题目,三角形和平行四边形的面积相等,因此:
(b × h1) ÷ 2 = b × h2
两边同时乘以2得到:
b × h1 = 2 × b × h2
由于底边 b 不为零,可以两边同时除以 b,得到:
h1 = 2 × h2
即 h1/h2 = 2/1
所以,三角形的高与平行四边形的高的比是 2:1。
【答案】:2:1
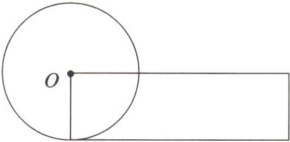
三、如下图,圆的周长是6.28cm,圆的面积和长方形面积相等,求长方形的周长。

答案:
【解析】:已知圆的周长是$6.28\,\text{cm}$,根据圆的周长公式$C = 2\pi r$(其中$C$为周长,$r$为半径,$\pi$取$3.14$),可得圆的半径$r = 6.28÷(2×3.14)=1\,\text{cm}$。
圆的面积公式为$S=\pi r^2$,则圆的面积$S = 3.14×1^2=3.14\,\text{cm}^2$。因为圆的面积和长方形面积相等,所以长方形面积也是$3.14\,\text{cm}^2$。
由图可知,长方形的宽等于圆的半径,即宽为$1\,\text{cm}$。根据长方形面积公式$S = 长×宽$,可得长方形的长为$3.14÷1 = 3.14\,\text{cm}$。
长方形的周长公式为$C=(长 + 宽)×2$,所以长方形的周长为$(3.14 + 1)×2=8.28\,\text{cm}$。
【答案】:8.28
圆的面积公式为$S=\pi r^2$,则圆的面积$S = 3.14×1^2=3.14\,\text{cm}^2$。因为圆的面积和长方形面积相等,所以长方形面积也是$3.14\,\text{cm}^2$。
由图可知,长方形的宽等于圆的半径,即宽为$1\,\text{cm}$。根据长方形面积公式$S = 长×宽$,可得长方形的长为$3.14÷1 = 3.14\,\text{cm}$。
长方形的周长公式为$C=(长 + 宽)×2$,所以长方形的周长为$(3.14 + 1)×2=8.28\,\text{cm}$。
【答案】:8.28
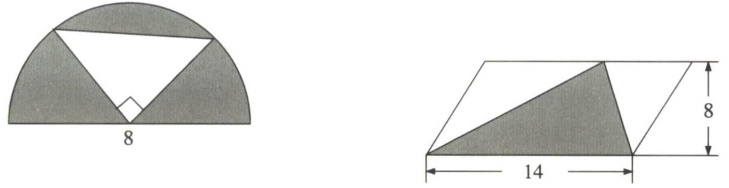
四、求下面图形中阴影部分的面积。(单位:cm)

答案:
【解析】:
左图阴影部分面积:
1. 半圆直径为8cm,半径$r = 8÷2 = 4$cm,半圆面积$S_{半圆}=\frac{1}{2}\pi r^{2}=\frac{1}{2}×3.14×4^{2}=25.12$cm²。
2. 空白三角形为等腰直角三角形,直角边等于半径4cm,面积$S_{三角形}=\frac{1}{2}×4×4 = 8$cm²。
3. 阴影面积$=25.12 - 8=17.12$cm²。
右图阴影部分面积:
1. 平行四边形底14cm,高8cm,面积$S_{平行四边形}=14×8 = 112$cm²。
2. 阴影三角形与平行四边形等底等高,面积$S_{阴影}=\frac{1}{2}×14×8 = 56$cm²。
两阴影部分总面积$17.12 + 56=73.12$cm²。
【答案】:73.12
左图阴影部分面积:
1. 半圆直径为8cm,半径$r = 8÷2 = 4$cm,半圆面积$S_{半圆}=\frac{1}{2}\pi r^{2}=\frac{1}{2}×3.14×4^{2}=25.12$cm²。
2. 空白三角形为等腰直角三角形,直角边等于半径4cm,面积$S_{三角形}=\frac{1}{2}×4×4 = 8$cm²。
3. 阴影面积$=25.12 - 8=17.12$cm²。
右图阴影部分面积:
1. 平行四边形底14cm,高8cm,面积$S_{平行四边形}=14×8 = 112$cm²。
2. 阴影三角形与平行四边形等底等高,面积$S_{阴影}=\frac{1}{2}×14×8 = 56$cm²。
两阴影部分总面积$17.12 + 56=73.12$cm²。
【答案】:73.12
查看更多完整答案,请扫码查看


