2025年开心假期暑假作业武汉出版社六年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年开心假期暑假作业武汉出版社六年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 一个最简真分数,分子与分母的和是 12,这样的分数的个数是(
A.1
B.2
C.3
B
)。A.1
B.2
C.3
答案:
【解析】:
首先,明确最简真分数的定义:分子和分母互质(即最大公因数为1),且分子小于分母。
设这个最简真分数为a/b,其中a为分子,b为分母。
根据题意,a+b=12,且a<b,a和b互质。
那么,可以列举出所有满足a+b=12,且a<b的整数对(a, b):
(1, 11),(2, 10),(3, 9),(4, 8),(5, 7)。
接下来,检查这些整数对中,哪些满足a和b互质的条件:
(1, 11):1和11互质,满足条件。
(2, 10):2和10有公因数2,不满足条件。
(3, 9):3和9有公因数3,不满足条件。
(4, 8):4和8有公因数4,不满足条件。
(5, 7):5和7互质,满足条件。
因此,满足条件的最简真分数有1/11和5/7,共2个。
【答案】:B
首先,明确最简真分数的定义:分子和分母互质(即最大公因数为1),且分子小于分母。
设这个最简真分数为a/b,其中a为分子,b为分母。
根据题意,a+b=12,且a<b,a和b互质。
那么,可以列举出所有满足a+b=12,且a<b的整数对(a, b):
(1, 11),(2, 10),(3, 9),(4, 8),(5, 7)。
接下来,检查这些整数对中,哪些满足a和b互质的条件:
(1, 11):1和11互质,满足条件。
(2, 10):2和10有公因数2,不满足条件。
(3, 9):3和9有公因数3,不满足条件。
(4, 8):4和8有公因数4,不满足条件。
(5, 7):5和7互质,满足条件。
因此,满足条件的最简真分数有1/11和5/7,共2个。
【答案】:B
3. 一个数的倒数是 2.4,另一个数的倒数是$1\frac{3}{5}$,这两个数的和是(
A.4
B.$1\frac{1}{24}$
C.$\frac{1}{4}$
$1\frac{1}{24}$
)。A.4
B.$1\frac{1}{24}$
C.$\frac{1}{4}$
答案:
【解析】:
首先,一个数的倒数是2.4,即这个数为$\frac{1}{2.4}$。为了方便计算,将2.4转换为分数形式,即$2.4 = \frac{12}{5}$。
所以,这个数为$\frac{1}{\frac{12}{5}} = \frac{5}{12}$。
接着,另一个数的倒数是$1\frac{3}{5}$,转换为假分数为$\frac{8}{5}$。
所以,另一个数为$\frac{1}{\frac{8}{5}} = \frac{5}{8}$。
最后,求这两个数的和:
$\frac{5}{12} + \frac{5}{8} = \frac{5 × 2}{12 × 2} + \frac{5 × 3}{8 × 3} = \frac{10}{24} + \frac{15}{24} = \frac{25}{24} = 1\frac{1}{24}$。
【答案】:B
首先,一个数的倒数是2.4,即这个数为$\frac{1}{2.4}$。为了方便计算,将2.4转换为分数形式,即$2.4 = \frac{12}{5}$。
所以,这个数为$\frac{1}{\frac{12}{5}} = \frac{5}{12}$。
接着,另一个数的倒数是$1\frac{3}{5}$,转换为假分数为$\frac{8}{5}$。
所以,另一个数为$\frac{1}{\frac{8}{5}} = \frac{5}{8}$。
最后,求这两个数的和:
$\frac{5}{12} + \frac{5}{8} = \frac{5 × 2}{12 × 2} + \frac{5 × 3}{8 × 3} = \frac{10}{24} + \frac{15}{24} = \frac{25}{24} = 1\frac{1}{24}$。
【答案】:B
4. 从甲地到乙地客车要行驶 5 小时,货车要行驶 6 小时,客车与货车速度的比是(
A.$5:6$
B.$6:5$
C.$5:11$
B
)。A.$5:6$
B.$6:5$
C.$5:11$
答案:
【解析】:设甲地到乙地的距离为$d$公里。根据题意,客车行驶这段距离需要5小时,货车需要6小时。因此,客车的速度为$v_1 = \frac{d}{5}$公里/小时,货车的速度为$v_2 = \frac{d}{6}$公里/小时。客车与货车速度的比为$\frac{v_1}{v_2} = \frac{\frac{d}{5}}{\frac{d}{6}} = \frac{6}{5}$。
【答案】:B
【答案】:B
四、如果整张方格纸的面积是 1,按要求表示阴影部分的面积。
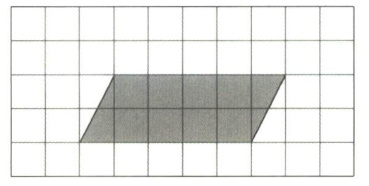
用分数表示是(
用小数表示是(
用百分数表示是(
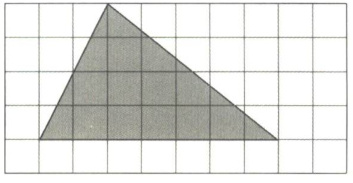
用分数表示是(
用小数表示是(
用百分数表示是(

用分数表示是(
$\frac{1}{5}$
)。用小数表示是(
0.2
)。用百分数表示是(
20%
)。
用分数表示是(
$\frac{9}{40}$
)。用小数表示是(
0.225
)。用百分数表示是(
22.5%
)。
答案:
【解析】:假设每个小方格的边长为1,先确定方格纸的总格数。观察插图,每张方格纸横向有8格,纵向有5格,所以总面积为$8×5 = 40$,即总格数为40,因为整张方格纸面积是1,所以每个小方格面积是$\frac{1}{40}$。
对于第一个阴影部分(平行四边形):底占4格,高占2格,面积为$4×2 = 8$个小方格。其面积用分数表示为$\frac{8}{40}=\frac{1}{5}$,小数表示为$1÷5 = 0.2$,百分数表示为$0.2×100\% = 20\%$。
对于第二个阴影部分(三角形):底占6格,高占3格,面积为$\frac{1}{2}×6×3 = 9$个小方格。其面积用分数表示为$\frac{9}{40}$,小数表示为$9÷40 = 0.225$,百分数表示为$0.225×100\% = 22.5\%$。
【答案】:$\frac{1}{5}$,0.2,20%,$\frac{9}{40}$,0.225,22.5%
对于第一个阴影部分(平行四边形):底占4格,高占2格,面积为$4×2 = 8$个小方格。其面积用分数表示为$\frac{8}{40}=\frac{1}{5}$,小数表示为$1÷5 = 0.2$,百分数表示为$0.2×100\% = 20\%$。
对于第二个阴影部分(三角形):底占6格,高占3格,面积为$\frac{1}{2}×6×3 = 9$个小方格。其面积用分数表示为$\frac{9}{40}$,小数表示为$9÷40 = 0.225$,百分数表示为$0.225×100\% = 22.5\%$。
【答案】:$\frac{1}{5}$,0.2,20%,$\frac{9}{40}$,0.225,22.5%
1. 把下面各数按从小到大的顺序排列。
(1)$167\%,1\frac{2}{5},1.6,1.606,\frac{1}{6}$
(
(2)$4.3,4\frac{1}{3},4.34,4\frac{1}{4}$
(
(1)$167\%,1\frac{2}{5},1.6,1.606,\frac{1}{6}$
(
$\frac{1}{6}$
)<($1\frac{2}{5}$
)<($1.6$
)<($1.606$
)<($167\%$
)(2)$4.3,4\frac{1}{3},4.34,4\frac{1}{4}$
(
$4\frac{1}{4}$
)<($4.3$
)<($4\frac{1}{3}$
)<($4.34$
)
答案:
【解析】:
(1)首先,我们需要将所有的数转换为小数形式,以便比较大小。
$167\% = 1.67$
$1\frac{2}{5} = 1 + \frac{2}{5} = 1.4$
$1.6$ 保持不变
$1.606$ 保持不变
$\frac{1}{6} = 0.1666...$ ,可以近似为 $0.167$(为比较而取足够多的小数位)
按照从小到大的顺序排列为:
$0.167 < 1.4 < 1.6 < 1.606 < 1.67$
即:
$\frac{1}{6} < 1\frac{2}{5} < 1.6 < 1.606 < 167\%$
(2)同样,我们将所有的数转换为小数形式(或保持其原有形式以便直接比较)。
$4.3$ 保持不变
$4\frac{1}{3} = 4 + \frac{1}{3} = 4.3333...$ ,可以近似为 $4.333$(为比较而取足够多的小数位)
$4.34$ 保持不变
$4\frac{1}{4} = 4 + \frac{1}{4} = 4.25$
按照从小到大的顺序排列为:
$4.25 < 4.3 < 4.333 < 4.34$
即:
$4\frac{1}{4} < 4.3 < 4\frac{1}{3} < 4.34$
【答案】:
(1)$\frac{1}{6}$;$1\frac{2}{5}$;$1.6$;$1.606$;$167\%$
(2)$4\frac{1}{4}$;$4.3$;$4\frac{1}{3}$;$4.34$
(1)首先,我们需要将所有的数转换为小数形式,以便比较大小。
$167\% = 1.67$
$1\frac{2}{5} = 1 + \frac{2}{5} = 1.4$
$1.6$ 保持不变
$1.606$ 保持不变
$\frac{1}{6} = 0.1666...$ ,可以近似为 $0.167$(为比较而取足够多的小数位)
按照从小到大的顺序排列为:
$0.167 < 1.4 < 1.6 < 1.606 < 1.67$
即:
$\frac{1}{6} < 1\frac{2}{5} < 1.6 < 1.606 < 167\%$
(2)同样,我们将所有的数转换为小数形式(或保持其原有形式以便直接比较)。
$4.3$ 保持不变
$4\frac{1}{3} = 4 + \frac{1}{3} = 4.3333...$ ,可以近似为 $4.333$(为比较而取足够多的小数位)
$4.34$ 保持不变
$4\frac{1}{4} = 4 + \frac{1}{4} = 4.25$
按照从小到大的顺序排列为:
$4.25 < 4.3 < 4.333 < 4.34$
即:
$4\frac{1}{4} < 4.3 < 4\frac{1}{3} < 4.34$
【答案】:
(1)$\frac{1}{6}$;$1\frac{2}{5}$;$1.6$;$1.606$;$167\%$
(2)$4\frac{1}{4}$;$4.3$;$4\frac{1}{3}$;$4.34$
2. 如果$a+\frac{3}{4}= b+\frac{4}{5}= c+\frac{5}{6}= d+\frac{6}{7}$,那么$a,b,c,d$中哪一个数最大?
答案:
【解析】:
首先,我们设 $ a + \frac{3}{4} = b + \frac{4}{5} = c + \frac{5}{6} = d + \frac{6}{7} = k $。
那么,我们可以分别解出 $ a, b, c, d $:
$ a = k - \frac{3}{4} $
$ b = k - \frac{4}{5} $
$ c = k - \frac{5}{6} $
$ d = k - \frac{6}{7} $
接下来,我们需要比较这些数的大小。为了比较它们的大小,我们可以比较它们减去 $ k $ 后的部分,即比较 $-\frac{3}{4}, -\frac{4}{5}, -\frac{5}{6}, -\frac{6}{7}$ 的大小。
为了更容易地比较这些分数,我们可以找到它们的最小公倍数(LCM)作为通分母。4, 5, 6, 7 的 LCM 是 420。
$-\frac{3}{4} = -\frac{3 × 105}{4 × 105} = -\frac{315}{420}$
$-\frac{4}{5} = -\frac{4 × 84}{5 × 84} = -\frac{336}{420}$
$-\frac{5}{6} = -\frac{5 × 70}{6 × 70} = -\frac{350}{420}$
$-\frac{6}{7} = -\frac{6 × 60}{7 × 60} = -\frac{360}{420}$
由于分母相同,我们只需要比较分子。分子越小,整个分数就越大(因为我们是比较负数)。
从上面的计算中,我们可以看到 $-\frac{3}{4}$ 的分子最小,所以 $-\frac{3}{4}$ 是这些数中最大的,即$a$ 是 $ a, b, c, d $ 中最大的。
【答案】:$a$
首先,我们设 $ a + \frac{3}{4} = b + \frac{4}{5} = c + \frac{5}{6} = d + \frac{6}{7} = k $。
那么,我们可以分别解出 $ a, b, c, d $:
$ a = k - \frac{3}{4} $
$ b = k - \frac{4}{5} $
$ c = k - \frac{5}{6} $
$ d = k - \frac{6}{7} $
接下来,我们需要比较这些数的大小。为了比较它们的大小,我们可以比较它们减去 $ k $ 后的部分,即比较 $-\frac{3}{4}, -\frac{4}{5}, -\frac{5}{6}, -\frac{6}{7}$ 的大小。
为了更容易地比较这些分数,我们可以找到它们的最小公倍数(LCM)作为通分母。4, 5, 6, 7 的 LCM 是 420。
$-\frac{3}{4} = -\frac{3 × 105}{4 × 105} = -\frac{315}{420}$
$-\frac{4}{5} = -\frac{4 × 84}{5 × 84} = -\frac{336}{420}$
$-\frac{5}{6} = -\frac{5 × 70}{6 × 70} = -\frac{350}{420}$
$-\frac{6}{7} = -\frac{6 × 60}{7 × 60} = -\frac{360}{420}$
由于分母相同,我们只需要比较分子。分子越小,整个分数就越大(因为我们是比较负数)。
从上面的计算中,我们可以看到 $-\frac{3}{4}$ 的分子最小,所以 $-\frac{3}{4}$ 是这些数中最大的,即$a$ 是 $ a, b, c, d $ 中最大的。
【答案】:$a$
查看更多完整答案,请扫码查看


