《2025年快乐假期衔接优化训练六年级数学》

1. 一辆公共汽车从起点站开出后,途中经过6个停靠站,最后到达终点站。下表记录了这辆公共汽车全程载客数量的变化情况。

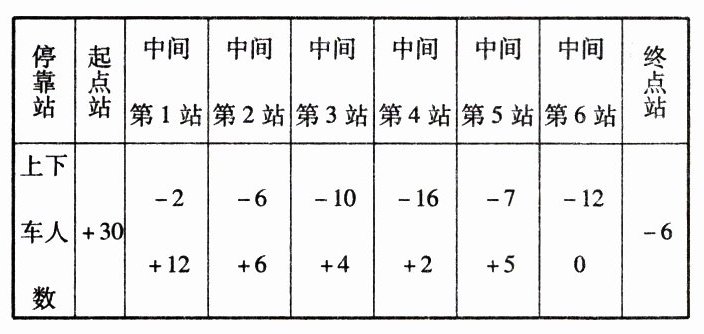
(1)中间的6个站中第1站上车的人数最多？第4站下车的人数最多？
(2)第6站只有乘客下车,没有乘客上车？
(3)经过第2站后车上还有40人？经过第5站后车上还有18人？
(4)你还能提出什么问题？并解答。
问题：经过第3站后车上比经过第2站后车上少多少人？
解答：经过第2站后车上40人，经过第3站后车上34人，40-34=6（人）。

答案： 1.
(1)
上车人数：比较$+12$，$+6$，$+4$，$+2$，$+5$，$0$的大小，$12\gt6\gt5\gt4\gt2\gt0$，所以中间第$1$站上车人数最多；
下车人数：比较$\vert - 2\vert$，$\vert - 6\vert$，$\vert - 10\vert$，$\vert - 16\vert$，$\vert - 7\vert$，$\vert - 12\vert$的大小，$16\gt12\gt10\gt7\gt6\gt2$，所以中间第$4$站下车人数最多。
(2)
观察表格，中间第$6$站上车人数为$0$，下车人数为$-12$，所以第$6$站只有乘客下车，没有乘客上车。
(3)
经过第$1$站后车上人数：$30 + 12-2=40$（人）；
经过第$2$站后车上人数：$40+6 - 6=40$（人）；
经过第$3$站后车上人数：$40+4 - 10=34$（人）；
经过第$4$站后车上人数：$34+2 - 16=20$（人）；
经过第$5$站后车上人数：$20+5 - 7=18$（人）。
(4)
问题：经过第$3$站后车上比经过第$2$站后车上少多少人？
解答：经过第$2$站后车上$40$人，经过第$3$站后车上$34$人，$40-34 = 6$（人）。
综上，答案依次为：
(1)中间第$1$站上车人数最多，中间第$4$站下车人数最多；
(2)第$6$站；
(3)经过第$2$站后车上还有$40$人，经过第$5$站后车上还有$18$人；
(4)答案不唯一，如上述所提问题及解答。

2. 下面是六(1)班6名女同学的身高。以她们的平均身高为标准,把平均身高记为0cm,超过的身高记为正,不足的身高记为负,用正负数表示她们的身高。

+6，-2，-11，-4，+8，+3，0

答案： 1. 首先求平均身高：
平均身高$\bar{x}=\frac{160 + 152+143 + 150+162+157}{6}$。
先计算分子：$160 + 152+143 + 150+162+157=(160 + 150)+(152 + 157)+(143 + 162)=310+309+305 = 924$。
则平均身高$\bar{x}=\frac{924}{6}=154\mathrm{cm}$。
2. 然后用正负数表示身高：
$1$号：$160−154 = + 6$；
$2$号：$152−154=-2$；
$3$号：$143−154=-11$；
$4$号：$150−154=-4$；
$5$号：$162−154 = + 8$；
$6$号：$157−154 = + 3$。
所以从左到右依次为$+6$，$-2$，$-11$，$-4$，$+8$，$+3$，$0$。

3. 体育课上,某中学对七年级男生进行了引体向上测试,以能做7个为标准。多于标准的次数记为正数,不足的次数记为负数,其中8名男生的成绩为+2,-1,+3,0,-2,-3,+1,0。
(1)这8名男生中达到标准的占百分之几？
(2)他们共做了多少次引体向上？
(3)你还能提出什么问题？并解答。

答案： 【解析】：
1. 首先明确达标的标准和判断达标的方法：
以能做$7$个为标准，成绩记为非负数（即大于等于$0$）的男生达到标准。
观察$8$名男生的成绩$ + 2$，$-1$，$ + 3$，$0$，$-2$，$-3$，$ + 1$，$0$，其中成绩为$ + 2$，$ + 3$，$0$，$ + 1$，$0$的$5$名男生达到标准。
2. 然后计算达到标准的男生所占百分比：
达到标准的男生所占百分比$=\frac{达到标准的人数}{总人数}×100\%$，总人数是$8$人，达到标准的人数是$5$人，所以达到标准的占$\frac{5}{8}×100\% = 62.5\%$。
3. 接着计算$8$名男生共做引体向上的次数：
先计算$8$名男生与标准次数的差值的和，再加上$8$名男生按标准应做的总次数。
$8$名男生与标准次数的差值分别为$+2$，$-1$，$ + 3$，$0$，$-2$，$-3$，$ + 1$，$0$，它们的和为$( + 2)+(-1)+( + 3)+0+(-2)+(-3)+( + 1)+0=(2 + 3+1)+(-1-2 - 3)+0=6 - 6+0 = 0$。
因为以$7$个为标准，$8$名男生按标准应做$7×8 = 56$次，所以他们共做了$56+0 = 56$次引体向上。
4. 最后提出问题并解答：
问题：这$8$名男生中成绩最好的比成绩最差的多做了多少次引体向上？
成绩最好的是$ + 3$，表示做了$7 + 3=10$次；成绩最差的是$-3$，表示做了$7-3 = 4$次。
则成绩最好的比成绩最差的多做了$10 - 4 = 6$次。
【答案】：
(1)$62.5\%$
(2)$56$次
(3)问题：这$8$名男生中成绩最好的比成绩最差的多做了多少次引体向上？答案：$6$次。