《2025年快乐假期衔接优化训练六年级数学》

7. 规定10吨记为0吨,11吨记为+1吨,则下列说法错误的是(A)。
A.8吨记为-8吨
B.15吨记为+5吨
C.6吨记为-4吨
D.+3吨表示重量为13吨

答案： A

8. 有下列四个式子；①$(-5)+(+3)= -8$；②$-(-2)^{3}= 6$；③$(+\frac {5}{6})+(-\frac {1}{6})= \frac {2}{3}$；④$-3÷(-\frac {1}{3})= 9$。其中,正确的有(C)
A.0个
B.1个
C.2个
D.3个

答案： C

四、用“＞、＜、=”号填空。
1. -0.02＜1
2. $\frac {4}{5}$＞$\frac {3}{4}$
3. $-\frac {22}{7}$＜-3.14
4. $-(-\frac {3}{4})$=$-[+(-0.75)]$

答案： ＜ ＞ ＜ =

1. 把下列数分类。
36,-9,0.7,+20.4,$-\frac {5}{6}$,100,-13,-261,+4.8,$\frac {10}{9}$,0
正数：36，0.7，+20.4，100，+4.8，$\frac{10}{9}$；负数：-9，$-\frac{5}{6}$，-13，-261。

答案： 【解析】：正数是大于$0$的数，负数是小于$0$的数，$0$既不是正数也不是负数。
$36\gt0$，$0.7\gt0$，$ +20.4\gt0$，$100\gt0$，$ +4.8\gt0$，$\frac{10}{9}\gt0$，所以这些数是正数；
$-9\lt0$，$-\frac{5}{6}\lt0$，$-13\lt0$，$-261\lt0$，所以这些数是负数。
【答案】：正数：$36$，$0.7$，$ +20.4$，$100$，$ +4.8$，$\frac{10}{9}$；负数：$-9$，$-\frac{5}{6}$，$-13$，$-261$。

2. 写出A、B、C、D、E、F点表示的数。

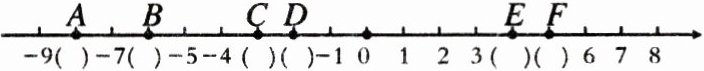
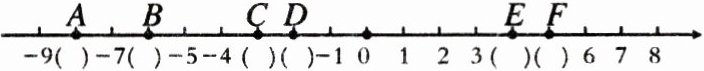
A:-8，B:-6，C:-4，D:-3，E:4，F:5

答案： 【解析】：观察数轴，数轴上每一大格表示$1$。
$A$点在$-9$和$-7$中间，所以$A$表示$-8$；
$B$点在$-7$和$-5$中间，所以$B$表示$-6$；
$C$点在$-4$的位置，所以$C$表示$-4$；
$D$点在$-4$和$-1$中间更靠近$-4$，且$-4$和$-1$中间间隔$3$格，每格表示$1$，所以$D$表示$-3$；
$E$点在$3$和$6$中间更靠近$3$，且$3$和$6$中间间隔$3$格，每格表示$1$，所以$E$表示$4$；
$F$点在$4$和$6$中间，所以$F$表示$5$。
【答案】：$-8$、$-6$、$-4$、$-3$、$4$、$5$

3. 在数轴上表示下列各数及它们的相反相数,并根据数轴上点的位置把它们按从小到大的顺序排列。
$-3\frac {1}{2}$,-|-2|,3,0,$1\frac {1}{2}$

$-3\frac{1}{2}＜-3＜-|-2|＜-1\frac{1}{2}＜0＜1\frac{1}{2}＜2＜3＜3\frac{1}{2}$

答案： 【解析】：
1. 先求各数的相反数：
$-3\frac{1}{2}$的相反数是$3\frac{1}{2}$；
$-\vert -2\vert=-2$，$-2$的相反数是$2$；
$3$的相反数是$-3$；
$0$的相反数是$0$；
$1\frac{1}{2}$的相反数是$-1\frac{1}{2}$。
2. 在数轴上表示这些数（略）。
3. 按从小到大的顺序排列：
负数小于$0$小于正数，两个负数比较绝对值大的反而小。
$\vert -3\frac{1}{2}\vert = 3\frac{1}{2}$，$\vert -3\vert = 3$，$\vert -2\vert = 2$，$\vert -1\frac{1}{2}\vert = 1\frac{1}{2}$。
所以$-3\frac{1}{2}＜-3＜-2＜-1\frac{1}{2}＜0＜1\frac{1}{2}＜2＜3＜3\frac{1}{2}$。
【答案】：$-3\frac{1}{2}＜-3＜-|-2|＜-1\frac{1}{2}＜0＜1\frac{1}{2}＜2＜3＜3\frac{1}{2}$

4. 比较下列各数的大小(要写出解题过程)。
(1)$-\frac {3}{11}$与-0.273
(2)$-|-2.65|与-(-2.6)$

答案： 【解析】：
(1) 先求出$\vert -\frac{3}{11}\vert$和$\vert - 0.273\vert$的值，再比较两个绝对值的大小，根据两个负数比较大小，绝对值大的反而小来判断$-\frac{3}{11}$与$-0.273$的大小。
$\vert -\frac{3}{11}\vert=\frac{3}{11}\approx0.2727$，$\vert - 0.273\vert = 0.273$。
因为$0.2727＜0.273$，即$\vert -\frac{3}{11}\vert＜\vert - 0.273\vert$，所以$-\frac{3}{11}＞-0.273$。
(2) 先分别化简$-\vert - 2.65\vert$与$-(-2.6)$，再根据正数大于负数来比较它们的大小。
$-\vert - 2.65\vert=-2.65$，$-(-2.6)=2.6$。
因为正数大于负数，所以$-2.65＜2.6$，即$-\vert - 2.65\vert＜-(-2.6)$。
【答案】：
(1)$-\frac{3}{11}＞-0.273$；
(2)$-\vert - 2.65\vert＜-(-2.6)$

五、计算下列各题。
$5+(-7)$ $(-3)-4-(-9)$
$-8-(-17)$ $6-(3-8)-|-7|$

答案： 【解析】：
1. 计算$5 + (-7)$：
根据有理数加法法则，异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值。$\vert -7\vert=7$，$\vert5\vert = 5$，$7＞5$，所以$5+(-7)=-(7 - 5)=-2$。
2. 计算$(-3)-4-(-9)$：
根据有理数减法法则，减去一个数等于加上这个数的相反数。则$(-3)-4-(-9)=(-3)+(-4)+9$，先计算$(-3)+(-4)=-(3 + 4)=-7$，再计算$-7 + 9=9-7 = 2$。
3. 计算$-8-(-17)$：
根据有理数减法法则，$-8-(-17)=-8 + 17=17-8 = 9$。
4. 计算$6-(3 - 8)-\vert -7\vert$：
先计算括号内的式子$3 - 8=-5$，再计算绝对值$\vert -7\vert = 7$，则原式变为$6-(-5)-7$，根据有理数减法法则$6-(-5)-7=6 + 5-7=11-7 = 4$。
【答案】：$-2$；$2$；$9$；$4$