2025年快乐假期衔接优化训练六年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐假期衔接优化训练六年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
3. 钟面上9点半时,时针和分针组成的角是(
A.锐角
B.直角
C.钝角
D.平角
C
)。A.锐角
B.直角
C.钝角
D.平角
答案:
3.C
4. 如图,$\angle AOE - \angle AOD$等于(
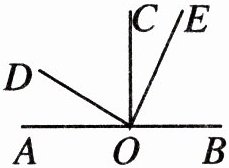
A.$\angle AOC$
B.$\angle BOC$
C.$\angle BOD$
D.$\angle EOD$
D
)
A.$\angle AOC$
B.$\angle BOC$
C.$\angle BOD$
D.$\angle EOD$
答案:
4.D
5. 把一个平形四边形任意分割成两个梯形,这两个梯形中(
A.面积
B.周长
C.高
D.上、下两底的和
C
)总是相等的。A.面积
B.周长
C.高
D.上、下两底的和
答案:
5.C
6. 等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(
A.24厘米
B.12厘米
C.18厘米
D.36厘米
B
)。A.24厘米
B.12厘米
C.18厘米
D.36厘米
答案:
6.B
四、操作练习。
1. 用量角器量出下面角的度数。

2. 画出$45^{\circ}$、$75^{\circ}$、$138^{\circ}$这三个角。
3. 过直线外一点,画这条直线的垂线和平行线。
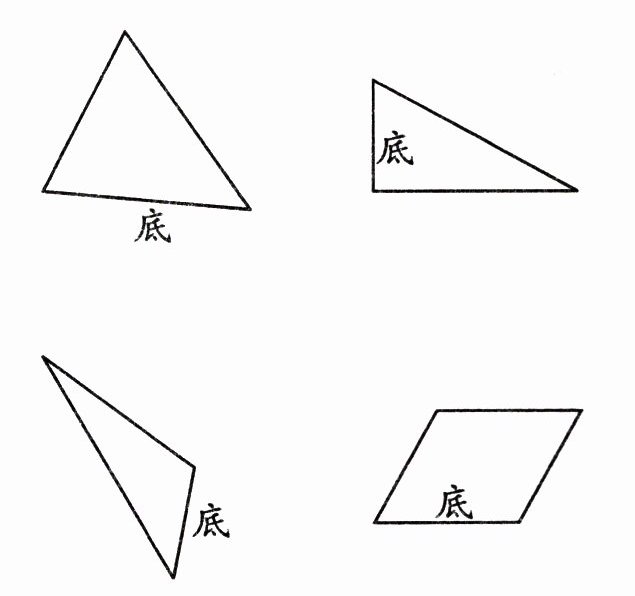
4. 作出下列每幅图形底边上的高。
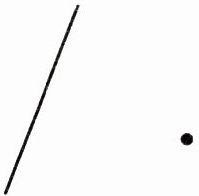
5. 画出点A到小河的最短路线。

1. 用量角器量出下面角的度数。

由于看不到插图中角的具体情况,无法准确量出度数。
2. 画出$45^{\circ}$、$75^{\circ}$、$138^{\circ}$这三个角。
画$45^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$45^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$45^{\circ}$角。画$75^{\circ}$角:因为$75^{\circ}=30^{\circ}+45^{\circ}$,先画$45^{\circ}$角,再以$45^{\circ}$角的一边为边,用量角器在其外部画$30^{\circ}$角,合起来就是$75^{\circ}$角。画$138^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$138^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$138^{\circ}$角。
3. 过直线外一点,画这条直线的垂线和平行线。

画垂线:把三角尺的一条直角边与已知直线重合,沿着直线移动三角尺,使三角尺的另一条直角边过直线外一点,沿着这条直角边画直线,就是已知直线的垂线。画平行线:把三角尺的一条直角边与已知直线重合,用直尺靠紧三角尺的另一条直角边,沿直尺移动三角尺,使三角尺原来和已知直线重合的直角边过直线外一点,沿这条直角边画直线,就是已知直线的平行线。
4. 作出下列每幅图形底边上的高。

由于看不到插图中图形的具体情况,无法准确作出底边上的高。一般作三角形底边上的高:从三角形的一个顶点向它的对边(或对边所在的直线)作垂线,顶点和垂足之间的线段叫做三角形的高。作平行四边形底边上的高:从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
5. 画出点A到小河的最短路线。

由于看不到插图中具体情况,点A到小河(可看作一条直线)的最短路线是点A到小河的垂线段。即过点A作小河(直线)的垂线,垂线段就是最短路线。
答案:
1. 由于看不到插图1中角的具体情况,无法准确量出度数。
2. 画$45^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$45^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$45^{\circ}$角。
画$75^{\circ}$角:因为$75^{\circ}=30^{\circ}+45^{\circ}$,先画$45^{\circ}$角,再以$45^{\circ}$角的一边为边,用量角器在其外部画$30^{\circ}$角,合起来就是$75^{\circ}$角。
画$138^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$138^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$138^{\circ}$角。
3. 画垂线:把三角尺的一条直角边与已知直线重合,沿着直线移动三角尺,使三角尺的另一条直角边过直线外一点,沿着这条直角边画直线,就是已知直线的垂线。
画平行线:把三角尺的一条直角边与已知直线重合,用直尺靠紧三角尺的另一条直角边,沿直尺移动三角尺,使三角尺原来和已知直线重合的直角边过直线外一点,沿这条直角边画直线,就是已知直线的平行线。
4. 由于看不到插图3中图形的具体情况,无法准确作出底边上的高。一般作三角形底边上的高:从三角形的一个顶点向它的对边(或对边所在的直线)作垂线,顶点和垂足之间的线段叫做三角形的高。作平行四边形底边上的高:从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
5. 由于看不到插图4中具体情况,点$A$到小河(可看作一条直线)的最短路线是点$A$到小河的垂线段。即过点$A$作小河(直线)的垂线,垂线段就是最短路线。
2. 画$45^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$45^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$45^{\circ}$角。
画$75^{\circ}$角:因为$75^{\circ}=30^{\circ}+45^{\circ}$,先画$45^{\circ}$角,再以$45^{\circ}$角的一边为边,用量角器在其外部画$30^{\circ}$角,合起来就是$75^{\circ}$角。
画$138^{\circ}$角:先画一条射线,将量角器的中心与射线的端点重合,$0^{\circ}$刻度线与射线重合,在量角器$138^{\circ}$刻度线的地方点一个点,以射线的端点为端点,通过刚才点的点,再画一条射线,就画出了$138^{\circ}$角。
3. 画垂线:把三角尺的一条直角边与已知直线重合,沿着直线移动三角尺,使三角尺的另一条直角边过直线外一点,沿着这条直角边画直线,就是已知直线的垂线。
画平行线:把三角尺的一条直角边与已知直线重合,用直尺靠紧三角尺的另一条直角边,沿直尺移动三角尺,使三角尺原来和已知直线重合的直角边过直线外一点,沿这条直角边画直线,就是已知直线的平行线。
4. 由于看不到插图3中图形的具体情况,无法准确作出底边上的高。一般作三角形底边上的高:从三角形的一个顶点向它的对边(或对边所在的直线)作垂线,顶点和垂足之间的线段叫做三角形的高。作平行四边形底边上的高:从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高。
5. 由于看不到插图4中具体情况,点$A$到小河(可看作一条直线)的最短路线是点$A$到小河的垂线段。即过点$A$作小河(直线)的垂线,垂线段就是最短路线。
1. 如图,直线AB、CD、EF都经过点O,且$AB \perp CD$,$\angle COE = 35^{\circ}$,求$\angle DOF$、$\angle BOF$的度数。

$\angle DOF=$

$\angle DOF=$
$35^{\circ}$
,$\angle BOF=$$125^{\circ}$
答案:
1.$∠DOF=35^{\circ}$ $∠BOF=125^{\circ}$
查看更多完整答案,请扫码查看


