《2025年快乐假期衔接优化训练六年级数学》

【例题1】有一个长方体,它的底面是一个正方形,它的表面积是190平方厘米,如果用一个平行于底面的平面将它截成两个长方体,则两个长方体表面积的和为240平方厘米,求原来长方体的体积。

答案： 【解析】：设原来长方体的底面边长为$a$厘米，高为$h$厘米。用平行于底面的平面将原长方体截成两个长方体后，增加的表面积就是两个截面的面积和，即$2a^{2}$平方厘米。已知原长方体表面积是$190$平方厘米，截成两个长方体后表面积和为$240$平方厘米，可据此列出方程$190 + 2a^{2}= 240$，求解可得$a^{2}= 25$，因为边长不能为负，所以$a = 5$厘米。又因为长方体表面积公式为$S = 2×$底面积$ + 4×$侧面积，即$2a^{2}+4ah = 190$，把$a = 5$代入该式，可得$h=\frac{190 - 2×25}{4×5}= 7$厘米。最后根据长方体体积公式$V = a^{2}h$，可算出原来长方体的体积。
【答案】：$175$立方厘米

【例题2】有大、中、小三个正方形水池,它们的内边长分别为4米、3米、2米,把两堆碎石分别沉没在中、小水池的水中,两个水池的水面分别升高了4厘米和11厘米。如果将这两堆碎石都沉没在大水池中,大水池水面将升高多少厘米？

答案： 【解析】：水池中水面升高部分水的体积就是投入水中的碎石体积。先分别计算沉入中、小水池中的碎石体积，中水池碎石体积为$3×3×0.04 = 0.36$立方米，小水池碎石体积为$2×2×0.11 = 0.44$立方米，两堆碎石体积之和为$0.36 + 0.44 = 0.8$立方米。把它们都沉入大池里，大池水面升高部分水的体积是$0.8$立方米，大池的底面面积是$4×4 = 16$平方米，根据水面升高高度=升高部分水的体积÷大池底面面积，可得大水池的水面升高$0.8÷16 = 0.05$米，因为$1$米=$100$厘米，所以$0.05$米换算为厘米是$0.05×100 = 5$厘米。
【答案】：5厘米

【例题3】判断：圆柱和圆锥都有无数条高。

答案： 【解析】：圆柱两个底面之间的距离叫做圆柱的高，两个底面之间有无数个对应的点，所以圆柱有无数条高；从圆锥的顶点到底面圆心的距离是圆锥的高，顶点和底面圆心都是唯一的点，所以圆锥只有一条高。
【答案】：错误

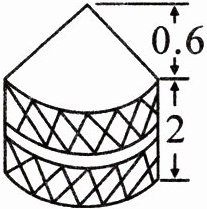
【例题4】一个稻谷囤,上面是圆锥体,下面是圆柱体(如下图)。圆柱的底面周长是9.42米,高2米,圆锥的高是0.6米。求这个粮囤的体积是多少立方米？

圆锥体化为圆柱体的高：$0.6×\frac{1}{3}=$0.2（米），底面积：$3.14×(\frac{9.42}{2×3.14})^{2}=$7.065（平方米），体积：$7.065×(2 + 0.2)=$15.543（立方米）。

答案： 【解析】：先根据圆锥体积公式与圆柱体积公式的关系，将圆锥转化为等底的圆柱，求出转化后圆柱的高，再根据圆的周长公式求出底面半径，进而求出底面积，最后根据圆柱体积公式求出总体积。
【答案】：圆锥体化为圆柱体的高：$0.6×\frac{1}{3}= 0.2$（米），底面积：$3.14×(\frac{9.42}{2×3.14})^{2}= 7.065$（平方米），体积：$7.065×(2 + 0.2)= 15.543$（立方米）。