《2025年快乐假期衔接优化训练六年级数学》

【例题1】数一数,图中一共有多少个角？

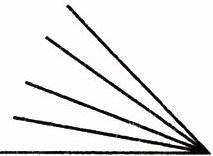
10

答案： 【解析】：这个图形是由一个顶点引出5条边构成的，由一个顶点引出两条边便组成一个角，这个图形包含的角较多，单个的较小的有4个；2个较小的角合成一个大角（2合1）的有3个，3合1的有2个，4合1的有1个。一共有$4 + 3 + 2 + 1 = 10$个角。
【答案】：10

【例题2】已知等腰三角形的一个角为$30^{\circ}$,求它的另外两个角各是多少度？

答案： 【解析】：此题已知等腰三角形的一个角为$30^{\circ}$，但未明确该角是顶角还是底角，所以需要分情况讨论。根据三角形内角和为$180^{\circ}$以及等腰三角形两底角相等的性质来计算另外两个角的度数。
【答案】：
(1)当$30^{\circ}$角为顶角时，另外两个角都是$75^{\circ}$；
(2)当$30^{\circ}$角为底角时，另外两个角分别是$30^{\circ}$和$120^{\circ}$。

【例题3】填空。
(1)圆的半径扩大3倍,直径就扩大(3)倍,周长就扩大(3)倍。
(2)一个圆的直径是10厘米,它的周长是(10π)厘米。

答案： 【解析】：第
(1)小题，因为在同一个圆中，直径$d = 2r$（$r$为半径），周长$C = 2\pi r=\pi d$，当半径扩大$3$倍时，新的半径为$3r$，则新的直径$d_{新}=2×(3r)=3×(2r)=3d$，新的周长$C_{新}=2\pi×(3r)=3×(2\pi r)=3C$，所以直径和周长都扩大$3$倍。第
(2)小题，已知圆的直径$d = 10$厘米，根据圆的周长公式$C=\pi d$，可得周长$C = 10\pi$厘米。
【答案】：
(1)3 3
(2)$10\pi$

【例题4】已知,如图,$AB // CD$。求证$\angle ABE + \angle BED + \angle EDC = 360^{\circ}$。



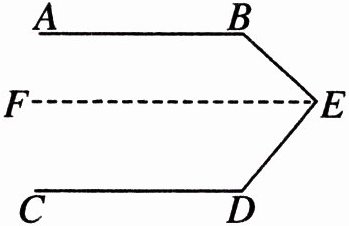
证明：过点$E$作$EF// AB$，利用平行线性质及平行传递性推出$\angle ABE+\angle BEF = 180^{\circ}$，$\angle FED+\angle EDC = 180^{\circ}$，再由$\angle BED=\angle BEF+\angle FED$，得$\angle ABE+\angle BED+\angle EDC = 360^{\circ}$。

答案： 【解析】：过点$E$作$EF// AB$。因为$AB// EF$（已作），所以$\angle ABE+\angle BEF = 180^{\circ}$（两直线平行，同旁内角互补）。因为$AB// EF$，$AB// CD$，所以$EF// CD$（平行于同一直线的两条直线平行），所以$\angle FED+\angle EDC = 180^{\circ}$（两直线平行，同旁内角互补）。所以$\angle ABE+\angle BEF+\angle FED+\angle EDC = 360^{\circ}$，又因为$\angle BED=\angle BEF+\angle FED$，所以$\angle ABE+\angle BED+\angle EDC = 360^{\circ}$。
【答案】：过点$E$作$EF// AB$，利用平行线性质及平行传递性推出$\angle ABE+\angle BEF = 180^{\circ}$，$\angle FED+\angle EDC = 180^{\circ}$，再由$\angle BED=\angle BEF+\angle FED$，得$\angle ABE+\angle BED+\angle EDC = 360^{\circ}$。