《2025年快乐假期衔接优化训练六年级数学》

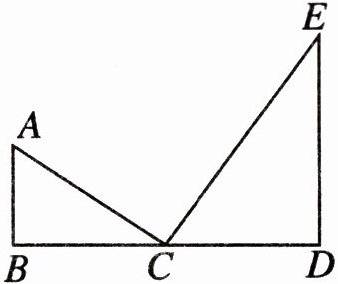
2. 如图,已知：$AC \perp CE$,$\angle E + \angle ECD = 90^{\circ}$,试简要证明：$\angle ACB = \angle E$。

证明：因为$AC\perp CE$，所以$\angle ACE = 90^{\circ}$，$\angle ACB+\angle ECD = 90^{\circ}$。又$\angle E+\angle ECD = 90^{\circ}$，根据同角的余角相等，所以$\angle ACB=\angle E$。

答案： 【解析】：
因为$AC\perp CE$，所以$\angle ACE = 90^{\circ}$，则$\angle ACB+\angle ECD = 180^{\circ}-\angle ACE=90^{\circ}$。
又因为$\angle E+\angle ECD = 90^{\circ}$，根据同角的余角相等，所以$\angle ACB=\angle E$。
【答案】：
因为$AC\perp CE$，所以$\angle ACE = 90^{\circ}$，$\angle ACB+\angle ECD = 90^{\circ}$。又$\angle E+\angle ECD = 90^{\circ}$，根据同角的余角相等，所以$\angle ACB=\angle E$。

3. 如图所示,$AB // CD$,P为AB,CD之间的一点,已知$\angle 1 = 32^{\circ}$,$\angle 2 = 25^{\circ}$,求$\angle BPC$的度数。(提示：作$PN // AB$)
解:如图所示,过点P作射线$PN// AB$
$\because AB// CD$(已知),
$\therefore PN// CD$(平行于同一条直线的两直线平行)
$\therefore ∠4=∠2=$25°(两直线平行,内错角相等)
$\because PN// AB$(已作),
$\therefore ∠3=∠1=$32°(两直线平行,内错角相等)
$\therefore ∠BPC=∠3+∠4=$32°+25°=57°

答案： 3.解:如图所示,过点P作射线$PN// AB$
$\because AB// CD$(已知),
$\therefore PN// CD$(平行于同一条直线的两直线平行)
$\therefore ∠4=∠2=25$。(两直线平行,内错角相等)
$\because PN// AB$(已作),
$\therefore ∠3=∠1=32^{\circ}$(两直线平行,内错角相等)
$\therefore ∠BPC=∠3+∠4=32^{\circ}+25^{\circ}=57^{\circ}$

六、求下面各图形中涂色部分的面积。
第一个图形涂色部分面积为1500cm²，第二个图形涂色部分面积为61cm²。

答案： 第一个图形
解：
梯形面积公式为$S_1=\frac{(a + b)h}{2}$（其中$a$、$b$为上底和下底，$h$为高），三角形面积公式为$S_2=\frac{1}{2}ah$（其中$a$为底，$h$为高）。
梯形的上底$a = 60cm$，下底$b = 80cm$，高$h = 30cm$，根据梯形面积公式可得梯形面积$S_{梯形}=\frac{(60 + 80)×30}{2}=2100cm^{2}$。
空白三角形的底$a = 60cm$，高$h = 20cm$，根据三角形面积公式可得空白三角形面积$S_{空白三角形}=\frac{1}{2}×60×20 = 600cm^{2}$。
涂色部分面积$S = S_{梯形}-S_{空白三角形}$，即$S=2100 - 600=1500cm^{2}$。
第二个图形
解：
可将图形分割为两个长方形。
上面长方形的长$a = 4cm$，宽$b = 4cm$，根据长方形面积公式$S = ab$，可得其面积$S_1=4×4 = 16cm^{2}$。
下面长方形的长$a = 15cm$，宽$b=(7 - 4)cm$，根据长方形面积公式可得其面积$S_2=15×(7 - 4)=45cm^{2}$。
涂色部分面积$S = S_1+S_2$，即$S=16 + 45=61cm^{2}$。
综上，第一个图形涂色部分面积为$\boldsymbol{1500cm^{2}}$，第二个图形涂色部分面积为$\boldsymbol{61cm^{2}}$。

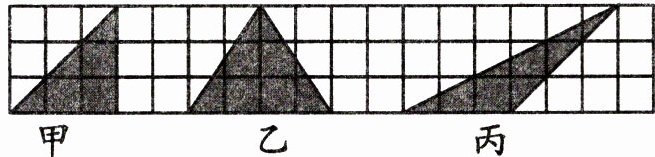
七、下列各阴影部分的面积有何关系？乙＞甲=丙

答案： 七、乙＞甲=丙

1. 毛毛说：“爷爷用一个可放大2倍的放大镜看一个$40^{\circ}$的角,结果这个角变成了$80^{\circ}$”你认为这种说法正确吗？为什么？

答案： 【解析】：角的大小取决于角的两条边张开的程度，张开的越大，角就越大，相反，张开的越小，角则越小。放大镜只是放大了角的边的长度，并不会改变角的两条边张开的程度，所以用放大镜看角，角的度数是不变的。因此，用一个可放大2倍的放大镜看一个$40^{\circ}$的角，这个角仍然是$40^{\circ}$，而不是$80^{\circ}$。
【答案】：这种说法不正确。因为角的大小只与角的两边张开的程度有关，放大镜放大的只是边的长度，而不是角两边张开的程度，所以用放大镜看角，角的度数不变，还是$40^{\circ}$。

2. 加工厂要制作一批长方体的录音机套,现量得它的长是60厘米,宽是20厘米,高是15厘米,做2500个这样的录音机套至少用布多少平方米？(没有底面)

答案： 【解析】：本题可先求出做一个录音机套所需布的面积，由于录音机套没有底面，所以求布的面积就是求这个长方体除底面之外的$5$个面的面积之和，再根据长方体表面积公式分别计算出各个面的面积并相加，最后乘以要制作的个数$2500$，将结果的单位换算为平方米即可。
- **步骤一：计算一个录音机套$5$个面的面积之和**
已知长方体录音机套的长是$60$厘米，宽是$20$厘米，高是$15$厘米。
根据长方形面积公式$S = ab$（其中$S$为长方形面积，$a$为长方形的长，$b$为长方形的宽），分别计算各个面的面积：
上面的面积：长$×$宽$= 60×20 = 1200$平方厘米。
前面和后面的面积：长$×$高$×2 = 60×15×2 = 1800$平方厘米。
左面和右面的面积：宽$×$高$×2 = 20×15×2 = 600$平方厘米。
将这$5$个面的面积相加，可得一个录音机套所需布的面积为：$1200 + 1800 + 600 = 3600$平方厘米。
- **步骤二：计算$2500$个录音机套所需布的面积**
一个录音机套需要布$3600$平方厘米，那么$2500$个录音机套所需布的面积为：$3600×2500 = 9000000$平方厘米。
- **步骤三：单位换算**
因为$1$平方米$ = 10000$平方厘米，所以将$9000000$平方厘米换算成平方米为：$9000000÷10000 = 900$平方米。
【答案】：$900$