《2025年超越训练七年级数学上册人教版四川专版》

1. 如图，点 $ B $，$ C $ 在线段 $ AD $ 上，$ AB:BC:CD = 3:2:5 $，$ E $，$ F $ 分别是 $ AB $，$ CD $ 的中点，且 $ EF = 24 $，求线段 $ BF $ 的长。

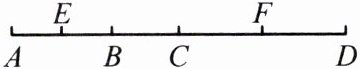
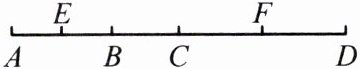
答案： 1.解:设$AB=3x$，$BC=2x$，$CD=5x$.因为$E$，$F$分别是$AB$，$CD$的中点，且$EF=24$，所以$EF=\frac{3}{2}x + 2x + \frac{5}{2}x = 24$，解得$x = 4$，所以$BF=BC + CF=2x+\frac{5}{2}x=\frac{9}{2}x=\frac{9}{2}×4 = 18$.

2. 如图，$ M $，$ N $ 为线段 $ AB $ 上的两点，且 $ AM:MB = 1:3 $，$ AN:NB = 5:7 $。若 $ MN = 2 $，求线段 $ AB $ 的长。

答案： 2.解:设$AM=x$，则$MB=3x$，$AB=x + 3x = 4x$.因为$AN:NB=5:7$，所以$AN=\frac{5}{12}AB=\frac{5}{12}×4x=\frac{5}{3}x$.因为$MN=AN - AM$，所以$\frac{5}{3}x - x = 2$，解得$x = 3$，所以$AB=4x = 12$.

3. 如图，$ C $，$ B $ 为线段 $ AD $ 上的两点，$ AB = CD $，$ BC = \frac{1}{3}AB $，$ M $，$ N $ 分别为 $ AB $，$ CD $ 的中点。若 $ MN = 14 $，求线段 $ AB $ 的长。

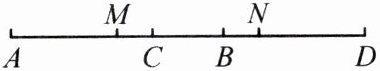
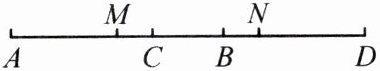
答案： 3.解:设$BC=x$，则$AB=CD=3x$，$AC=BD=2x$，所以$AM=\frac{1}{2}AB=\frac{3}{2}x$，$ND=\frac{1}{2}CD=\frac{3}{2}x$.因为$MN=AD - AM - ND = 14$，所以$5x - 2×\frac{3}{2}x = 14$，解得$x = 7$，所以$AB=3x = 21$.

4. 如图，点 $ B $，$ C $ 在线段 $ AD $ 上，$ CD = 2AB + 3 $。
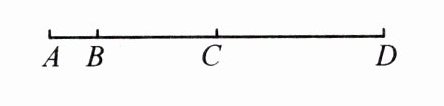
(1) 若 $ C $ 是线段 $ AD $ 的中点，求 $ BC - AB $ 的值；(2) 若 $ BC = \frac{1}{4}AD $，求 $ BC - AB $ 的值。

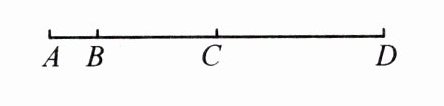
答案： 4.解:设$AB=x$，则$CD=2x + 3$.
(1)因为$C$是$AD$的中点，所以$AC=CD=2x + 3$，所以$BC=AC - AB=2x + 3 - x=x + 3$，所以$BC - AB=x + 3 - x = 3$.
(2)因为$BC=\frac{1}{4}AD$，所以$AB + CD=3BC$，即$x + 2x + 3 = 3BC$，所以$BC=x + 1$，所以$BC - AB=x + 1 - x = 1$.