《2025年超越训练七年级数学上册人教版四川专版》

5. 观察下面按一定规律排列的数：

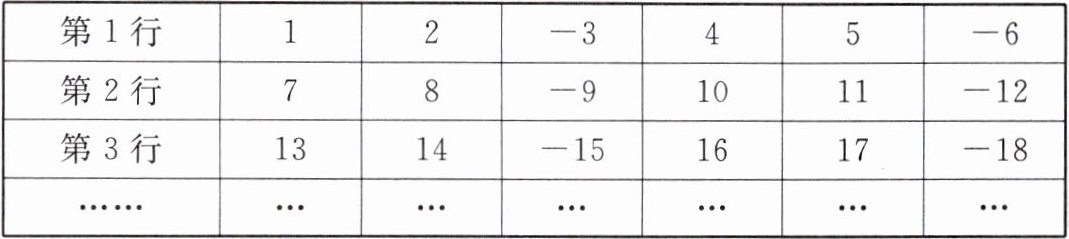
(1)第10行中最右边的数是-60,第11行中最左边的数是61.
(2)$-2025$这个数在第338行的第3列(从左往右数).
(3)在前2025个数中,正数有1350个,负数有675个.

答案： 5.
(1)-60 61
(2)338 3
(3)1 350 675

6. 将正整数1至2025按如表所示排列,记$a_{ij}$表示第$i$行第$j$列的数,如$a_{14}$表示第1行第4列的数是4.

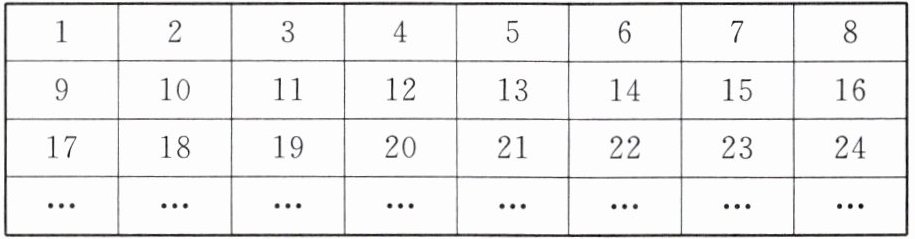
(1)$a_{32}=$18,$a_{55}=$37;
(2)若$a_{ij}=2024$,则$i=$253,$j=$8;
(3)用$i,j$表示$a_{ij}=$8(i - 1)+j.

答案： 6.
(1)18 37
(2)253 8
(3)8$(i - 1)+j$

7. 将连续正整数按如下规律排列：

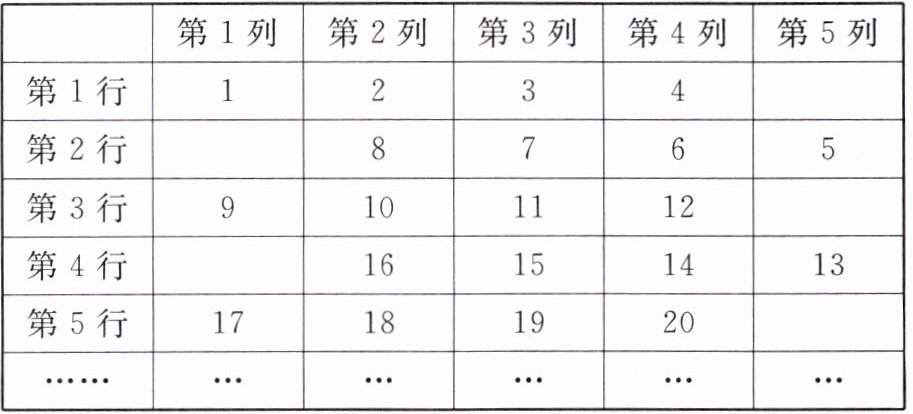
若正整数565位于第$a$行,第$b$列,则$a + b$的值是147.

答案： 7.147

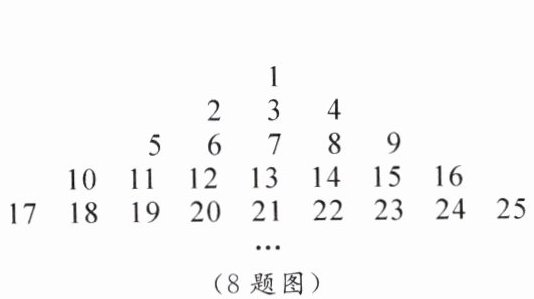
8. 如图所示的数阵由从1开始的连续自然数排列而成.
(1)第8行中的最后一个数是64,第8行中共有15个数;
(2)第$n$行中的第一个数是$(n - 1)^{2}+1$,最后一个数是$n^{2}$,第$n$行中共有$(2n - 1)$个数.

答案： 8.
(1)64 15
(2)$(n - 1)^{2}+1$ $n^{2}$ $(2n - 1)$

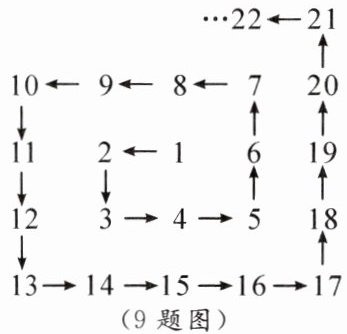
9. 将正整数从1开始按如图所示的规律排列成一个数阵,其中,2在第1个拐弯处,3在第2个拐弯处,5在第3个拐弯处$\cdots\cdots$则第2025个拐弯处的数是1026170.

答案： 9.1 026 170