《2025年超越训练七年级数学上册人教版四川专版》

5. 已知表示数$a$，$b$，$c$的点在数轴上的位置如图所示。
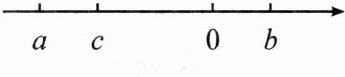
(1) 化简$2\vert b - c\vert-\vert b + c\vert+\vert a - c\vert-\vert a - b\vert$；
(2) 若$(c + 4)^2+\vert a + c + 10\vert = 0$，且$b=\vert a - c\vert$，求(1)中式子的值。

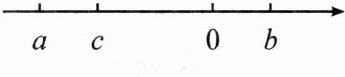
答案： 5.解：
(1)由图可得$b - c ＞ 0$，$b + c ＜ 0$，$a - c ＜ 0$，$a - b ＜ 0$，所以原式$=2(b - c) - (-b - c) + (c - a) - (b - a)= 2b - 2c + b + c + c - a - b + a = 2b$。
(2)由题意，得$c + 4 = 0$，$a + c + 10 = 0$，所以$c = -4$，$a = -6$，所以$b = \vert a - c\vert = \vert -6 - (-4)\vert = 2$，所以原式$= 2×2 = 4$。

6. 已知$x＜0＜z$，$xy＞0$，且$\vert y\vert＞\vert z\vert＞\vert x\vert$。
(1) 画出数轴，并在数轴上标出表示$x$，$y$，$z$的点的大致位置；
(2) 化简$\vert x + z\vert+2\vert y + z\vert-3\vert x - y\vert$；
(3) 求$\frac{x}{\vert x\vert}+\frac{y}{\vert y\vert}+\frac{z}{\vert z\vert}+\frac{xyz}{\vert xyz\vert}$的值。

答案： 6.解：
(1)如图所示.![img alt=图片编号或题号(图片的具体编号或者所属题目的题号)]
(2)由
(1)中的数轴可得$x + z ＞ 0$，$y + z ＜ 0$，$x - y ＞ 0$，所以原式$=(x + z) + 2(-y - z) - 3(x - y)= x + z - 2y - 2z - 3x + 3y = y - 2x - z$。
(3)因为$x ＜ 0$，$y ＜ 0$，$z ＞ 0$，所以$xyz ＞ 0$，所以原式$=\frac{x}{-x} + \frac{y}{-y} + \frac{z}{z} + \frac{xyz}{xyz} = -1 - 1 + 1 + 1 = 0$。

7. 已知$abc\neq0$，$a + b + c = 0$，则$\frac{\vert a\vert}{a}\frac{b}{\vert b\vert}+\frac{\vert b\vert}{b}\frac{c}{\vert c\vert}+\frac{\vert c\vert}{c}\frac{a}{\vert a\vert}$的值为-1。

答案： 7.$-1$

8. 若$abc\neq0$，$a + b + c = 0$，设$x=\frac{\vert a\vert}{b + c}+\frac{\vert b\vert}{c + a}+\frac{\vert c\vert}{a + b}$，求$x^2 - 99x + 2025$的值。

答案： 8.解：因为$abc ≠ 0$，$a + b + c = 0$，所以$a$，$b$，$c$的符号应是二正一负或二负一正。①当$a$，$b$，$c$的符号是二正一负时，设$a ＞ 0$，$b ＞ 0$，$c ＜ 0$，所以$x = \frac{\vert a\vert}{-a} + \frac{\vert b\vert}{-b} + \frac{\vert c\vert}{-c} = \frac{a}{-a} + \frac{b}{-b} + \frac{-c}{-c} = -1$，所以$x^{2} - 99x + 2025 = 1 + 99 + 2025 = 2125$。②当$a$，$b$，$c$的符号是二负一正时，设$a ＜ 0$，$b ＜ 0$，$c ＞ 0$，所以$x = \frac{\vert a\vert}{-a} + \frac{\vert b\vert}{-b} + \frac{\vert c\vert}{-c} = \frac{-a}{-a} + \frac{-b}{-b} + \frac{c}{-c} = 1$，所以$x^{2} - 99x + 2025 = 1 - 99 + 2025 = 1927$。