《2025年超越训练七年级数学上册人教版四川专版》

7. 观察如图所示的点阵图和相应的等式，探究其中的规律：
(1)分别在④和⑤后面的横线上写出相应的等式；
(2)猜想与第$n$个点阵图相应的等式是1+3+5+7+⋯+(2n-1)=n².

答案： 7.
(1)④1+3+5+7=4² ⑤1+3+5+7+9=5²
(2)1+3+5+7+⋯+(2n-1)=n²

8. 用棋子摆成的图案如图所示，摆第1个图案需要7枚棋子，摆第2个图案需要19枚棋子，摆第3个图案需要37枚棋子……按照这样的方式摆下去，摆第$n$个图案所需棋子的枚数为3n(n+1)+1.

答案： 8.3n(n+1)+1

9. 用棋子摆成的图案如图所示，第1个图案中有$a_{1}$枚棋子，第2个图案中有$a_{2}$枚棋子，第3个图案中有$a_{3}$枚棋子……$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+\cdots+\frac{1}{a_{2025}}$的值为\frac{2025}{2026}.

答案： $9.\frac{2025}{2026}$

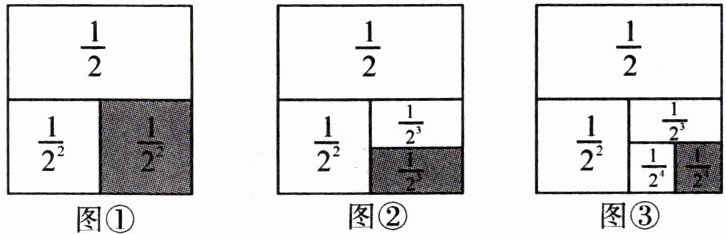
10. 如图①，将面积为1的大正方形平均分成两份，再将其中的一份又平均分成两份，则空白部分的面积可表示为$\frac{1}{2}+\frac{1}{2^{2}}=1-\frac{1}{2^{2}}$，以此类推，得到图②和图③.
(1)根据图形中的规律补全下面式子：
$\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}=$1-\frac{1}{2^{3}}，$\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\frac{1}{2^{4}}=$1-\frac{1}{2^{4}}.
(2)计算：$\frac{1}{2^{10}}+\frac{1}{2^{11}}+\cdots+\frac{1}{2^{20}}$.

答案： 10.解：$(1)1-\frac{1}{2^{3}},1-\frac{1}{2^{4}}.(2)$因为$\frac{1}{2}+\frac{1}{2^{2}}+\cdots+\frac{1}{2^{9}}=1-\frac{1}{2^{9}}，$
$\frac{1}{2}+\frac{1}{2^{2}}+\cdots+\frac{1}{2^{20}}=1-\frac{1}{2^{20}}，$所以$\frac{1}{2^{10}}+\frac{1}{2^{11}}+\cdots+\frac{1}{2^{20}}=\frac{1}{2}+\frac{1}{2^{2}}+\cdots+\frac{1}{2^{20}}-(\frac{1}{2}+\frac{1}{2^{2}}+\cdots+\frac{1}{2^{9}})=1-\frac{1}{2^{20}}-(1-\frac{1}{2^{9}})=$
$\frac{1}{2^{9}}-\frac{1}{2^{20}}.$

11. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1，3，6，10，…)和“正方形数”(如1，4，9，16，…).在小于200的数中，设最大的“三角形数”为$m$，最大的“正方形数”为$n$，求$m + n$的值.

答案： 11.解：由图可得第a个“三角形数”为$1+2+3+⋯+a=\frac{a(a+1)}{2}，$第a个“正方形数”为a².当a=19时，$\frac{a(a+1)}{2}=$
190＜200，当a=20时，\frac{a(a+1)}{2}=210＞200，所以m=190.当
a=14时，a²=196＜200，当a=15时，a²=225＞200，所以n=
196.所以m+n的值为190+196=386.