《2025年经纶学典提高班六年级数学上册苏教版》

1. 根据要求在合适的位置添上括号。
(1)最后一步求积: $\frac{1}{2} ÷ \frac{1}{4} + \frac{1}{4} × \frac{3}{5}$
(2)第一步求和: $\frac{1}{2} ÷ \frac{1}{4} + \frac{1}{4} × \frac{3}{5}$
(3)乘→加→除: $\frac{1}{2} ÷ \frac{1}{4} + \frac{1}{4} × \frac{3}{5}$

答案： 1.
(1)$\left(\frac{1}{2}÷\frac{1}{4}+\frac{1}{4}\right)×\frac{3}{5}$(答案不唯一)
(2)$\frac{1}{2}÷\left(\frac{1}{4}+\frac{1}{4}\right)×\frac{3}{5}$(答案不唯一)
(3)$\frac{1}{2}÷\left(\frac{1}{4}+\frac{1}{4}×\frac{3}{5}\right)$

2. 计算下面各题,能简算的要简算。
$3÷(\frac{5}{7}-\frac{3}{14})$
$[1-(\frac{1}{4}+\frac{3}{8})]÷\frac{1}{4}$
$\frac{4}{19}×\frac{5}{13}+\frac{4}{13}×\frac{8}{19}$
$2025×\frac{2023}{2024}$

答案： 2. 6 $\frac{3}{2}$ $\frac{4}{19}$ $2023\frac{2023}{2024}$

3. 解方程。
$\frac{2}{3}x+x= 12$
$x-\frac{3}{5}x= 30$

答案： 3. $x=\frac{36}{5}$ $x=75$

4. 求梯形的上底。

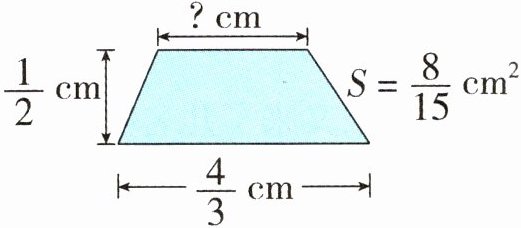
答案： 4. $\frac{8}{15}×2÷\frac{1}{2}-\frac{4}{3}=\frac{4}{5}$(厘米)

5. 城建工人铺一条自来水管道,前3天铺了$\frac{1}{2}$千米,后5天铺了$\frac{7}{10}$千米。城建工人平均每天铺多少千米?

答案： 5. $\left(\frac{1}{2}+\frac{7}{10}\right)÷(3+5)=\frac{3}{20}$(千米)答:城建工人平均每天铺$\frac{3}{20}$千米。

6. 下图是两种袋装饼干的规格和单价。

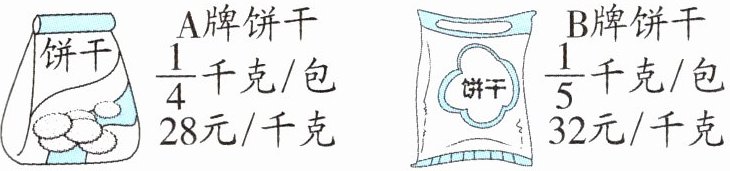
(1)两种饼干各买4包,一共重多少千克?
(2)买32包A牌饼干应付多少元?如果用这些钱买B牌饼干,可以买多少包?

答案： 6.
(1)$4×\left(\frac{1}{4}+\frac{1}{5}\right)=\frac{9}{5}$(千克)答:一共重$\frac{9}{5}$千克。
(2)$32×\frac{1}{4}×28=224$(元) $224÷32÷\frac{1}{5}=35$(包)答:买32包A牌饼干应付224元。如果用这些钱买B牌饼干,可以买35包。

7. 新素养 推理意识 三个连续偶数,最大的偶数是这三个数和的$\frac{2}{5}$,最大的偶数是(12)。

答案： 7. 12 提示:根据题意,设这三个连续的偶数分别是$2a-2$、$2a$、$2a+2$,因为最大数是三个偶数和的$\frac{2}{5}$,可以得到$(2a-2+2a+2a+2)×\frac{2}{5}=2a+2$,即$6a×\frac{2}{5}=2a+2$,等式两边同时乘5,得到$12a=10a+10$,等式两边同时减去$10a$,得到$2a=10$,解得$a=5$,最大的偶数就是$2a+2=2×5+2=12$。

8. 巧算:如果A与B互为倒数,那么$\frac{A}{8}×(\frac{3}{5}-\frac{1}{7})÷\frac{2}{B}$的结果是多少?

答案： 8. $\frac{1}{35}$ 提示:$\frac{A}{8}×\left(\frac{3}{5}-\frac{1}{7}\right)÷\frac{2}{B}=\frac{A}{8}×\frac{16}{35}×\frac{B}{2}=\frac{AB}{35}=\frac{1}{35}$。