《2025年经纶学典提高班六年级数学上册苏教版》

1. (1)(徐州铜陵真题)下列表述中,运用了假设策略解决问题的有(B)。
① 解决租船问题时在表格中罗列出所有的租船方案并进行比较分析。
② 在计算$762÷31$时,把除数当作30来试商。
③ 推导圆面积计算公式时,把圆剪拼成近似长方形。
④ 4个大盒和6个小盒共装了200个球,1个大盒比1个小盒多装20个,求每个大、小盒各能装多少个球。可以假设10个都是小盒,进行求解。
A.①②③
B.①②④
C.①③④
D.②③④

答案： B 提示:③运用的策略是“转化”，通过将圆剪拼成近似长方形，利用长方形的面积公式推出圆的面积公式。

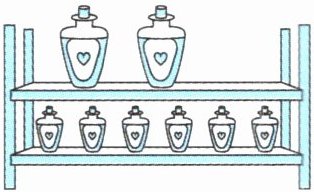
(2)(南通海安真题)下图架子上的药水共有1080毫升,每个小瓶里的药水是大瓶的$\frac{1}{3}$。下面说法中,正确的有(D)个。
① 可以看作12个小瓶里的药水有1080毫升。
② 可以看作4个大瓶里的药水有1080毫升。
③ 可以看作1个大瓶和3个小瓶共有药水540毫升。
④ 可以看作3个大瓶和3个小瓶共有药水1080毫升。

A.1
B.2
C.3
D.4

答案： D 提示:因为每个小瓶的药水是大瓶的$\frac{1}{3}$，也就是1个大瓶的药水等于3个小瓶的药水，2个大瓶的药水就是$2×3 = 6$(个)小瓶的药水，再加上下面的6个小瓶，一共是12个小瓶，即12个小瓶里药水有1080毫升，所以①说法正确；3个小瓶等于1个大瓶，6个小瓶相当于$6÷3 = 2$(个)大瓶，一共就是$2 + 2 = 4$(个)大瓶，即4个大瓶里的药水有1080毫升，②说法正确；1个大瓶和3个小瓶中药水的容积就是1080毫升的一半，$1080÷2 = 540$(毫升)，所以③说法正确；把其中的3个小瓶看成1个大瓶，就是3个大瓶和3个小瓶共有药水1080毫升，④说法正确，所以此题的正确选项是D。

2. (盐城大丰真题)为迎接阳光体育节,学校要为参加表演的学生统一购买演出服装,大号、中号、小号共240套,大号演出服比小号少60套,中号演出服比小号多45套。大号演出服购买了多少套?

答案： $240 + 60 - 45 = 255$(套) 小号:$255÷3 = 85$(套) 大号:$85 - 60 = 25$(套) 答:大号演出服购买了25套。 提示:根据题意，通过调整三种型号服装数量的差异，使它们都与小号服装数量建立联系，从而求出小号服装数量，进而得出大号服装数量。三种型号服装共240套，把大号比小号少的60套补上，把中号比小号多的45套减去，此时的总数就相当于3倍小号服装的数量。即$240 + 60 - 45 = 255$(套)，那么小号服装数量为$255÷3 = 85$(套)。因为大号演出服比小号少60套，所以大号服装数量为$85 - 60 = 25$(套)。

3. (南京秦淮真题)“双十一”期间,不少快递企业为环保助力。阳光快递开展“快递箱换鸡蛋”活动,请你参考下面的对话算一算,每个大纸箱能换多少个鸡蛋?每个小纸箱呢?
“我用2个大纸箱和6个小纸箱换了60个鸡蛋。”
“一个大纸箱比一个小纸箱多换2个鸡蛋。”

答案： 大纸箱:$(60 + 6×2)÷(6 + 2) = 9$(个) 小纸箱:$9 - 2 = 7$(个) 答:每个大纸箱能换9个鸡蛋，每个小纸箱能换7个鸡蛋。 提示:2个大纸箱 + 6个小纸箱 = 60个鸡蛋，一个大纸箱比一个小纸箱多换2个鸡蛋，那么6个大纸箱比6个小纸箱多换$6×2 = 12$(个)鸡蛋，得到$(2 + 6)$个大纸箱可以换$(60 + 12)$个鸡蛋，用除法计算出每个大纸箱能换鸡蛋的个数，再减去2，就得每个小纸箱可以换鸡蛋的个数。

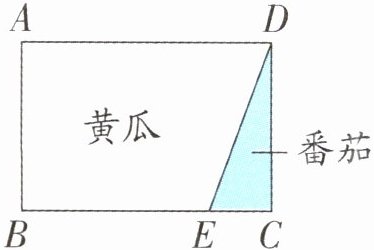
4. (无锡锡山真题)有一块长方形地,长20米。王大伯要把这块地划分成两部分,分别用来种黄瓜和番茄,并且要使种黄瓜的面积是种番茄的面积的7倍。用线段DE作为分割线(如图所示),请你计算出线段CE表示的实际长度。

答案：
$20×2÷(7 + 1)×1 = 5$(米) 答:线段CE表示的实际长度是5米。 提示:根据题意，把种植番茄的面积看作1份，那么种植黄瓜的面积占7份，这块地的面积一共是$7 + 1 = 8$(份)；过点E作AD的垂线段，如下图，得到三角形DEF面积也是1份，长方形CDFE的面积是2份，长方形CDFE与长方形ABCD面积的比 = $EC:BC = 2:(1 + 7)$，也就是把20米平均分成$(1 + 7)$份，CE占其中的2份，据此解答。