《2025年经纶学典提高班六年级数学上册苏教版》

1. 在括号里填上合适的数。
780 毫升= (0.78)升
5.1 立方分米= (5100)立方厘米
0.4 立方米= (400)立方分米= (400)升
6400 毫升= (6400)立方厘米= (6.4)升

答案： 1. 0.78 5100 400 400 6400 6.4

2. 妈妈做了一盘小乐爱吃的东坡肉(如图)。每小块肉可以看成是棱长约为5厘米的正方体。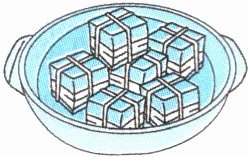
(1)要做这样一盘菜,妈妈需要买约(750)克的肉。(1 立方厘米约 1 克)
(2)每小块肉都需用棉线捆扎,打结处用去约3厘米的棉线。这盘肉至少需要用(258)厘米的棉线。

答案： 2.
(1)750
(2)258

3. 如图是一个正方体的展开图,你能根据已知条件求出它的表面积和体积吗?

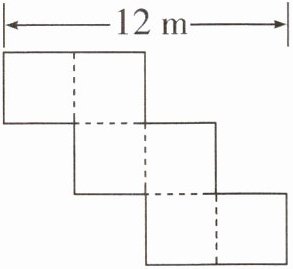
答案： 3. 12÷4=3(米) 表面积:3×3×6=54(平方米)
体积:3×3×3=27(立方米)
答:它的表面积是54平方米,体积是27立方米。

4. 新情境 图表信息 小李家的洗菜池是长方体形状,相关参数如图。
水槽尺寸:长760 mm 宽450 mm 深228 mm 板材材质:SUS304不锈钢
先给洗菜池里放20厘米深的水洗菜。如果洗菜池的下水管的排水速度是每秒0.3升,洗完菜后把这些水排干净,大约需要多少秒?(洗菜过程中损耗的水忽略不计)

答案： 4. 760毫米=76厘米 450毫米=45厘米 76×
45×20=68400(立方厘米) 68400立方厘米=68.4升
68.4÷0.3=228(秒) 答:大约需要228秒。

5. 一种肥皂的尺寸如左下图。美丽超市进行促销活动(买三送一),需要把4块这样的肥皂装在一个包装盒里。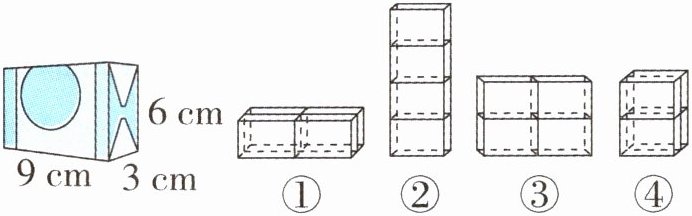
(1)思晴画出了上面四种包装方式的草图,第(④)种包装方式最省包装纸。
(2)(1)中所选包装方式每个包装盒至少需要多少平方厘米的包装纸?
3×2=6(厘米) 6×2=12(厘米) (9×6+9×12+6×12)×2=468(平方厘米)
答:每个包装盒至少需要468平方厘米的包装纸。

答案： 5.
(1)④
(2)3×2=6(厘米) 6×2=12(厘米) (9×6+9×
12+6×12)×2=468(平方厘米)
答:每个包装盒至少需要468平方厘米的包装纸。

6. 在一个长50厘米,宽40厘米的装有部分水的长方体玻璃缸中,放入一个棱长是10厘米的正方体铁块,铁块完全浸入,水未溢出,这时水深20厘米。若把这个铁块从缸中拿出来,则缸中的水面高多少厘米?
链接“提优秘籍”P5例3

答案： 6. 10×10×10=1000(立方厘米) 1000÷50÷40=
0.5(厘米) 20-0.5=19.5(厘米) 答:缸中的水面高19.5厘米。 提示:把铁块放入缸中后,水面上升的体积就是铁块的体积。利用正方体的体积公式即可求得铁块的体积,也就是水面上升的体积。再根据长方体的体积公式,即可求得水面上升的高度。最后用铁块完全浸入时水面的高度减去上升的高度即可。

7. 如果在一个长6厘米、宽5厘米、高3厘米的长方体的8个顶点处,分别截下一个棱长为1厘米的小正方体,那么剩下的立体图形的表面积是多少平方厘米?体积是多少立方厘米?

答案： 7. 表面积:(6×5+6×3+3×5)×2=126(平方厘米)
体积:6×5×3-8×1×1×1=82(立方厘米)
答:剩下的立体图形的表面积是126平方厘米,体积是82立方厘米。 提示:在长方体的8个顶点处分别截下一个棱长为1厘米的小正方体,剩下的部分的表面积与原长方体的表面积相同,由此利用长方体的表面积公式即可解答。剩下的体积等于原来长方体的体积与8个棱长为1厘米的小正方体的体积之差,据此利用长方体和正方体的体积公式计算即可解答。