《2025年经纶学典提高班六年级数学上册苏教版》

1. 计算下面各题。
$\frac{3}{8}×\frac{1}{6}×\frac{8}{9}$
$\frac{3}{26}×12×\frac{13}{4}$
$\frac{1}{16}×\frac{5}{27}×48$
$\frac{10}{21}×\frac{12}{25}×\frac{14}{15}$

答案： 1. $\frac{1}{18}$ $\frac{9}{2}$ $\frac{5}{9}$ $\frac{16}{75}$

2. 根据条件,把数量关系式补充完整。
(1)长方体中,长是宽的$\frac{4}{3}$,高是长的$\frac{2}{7}$。
(宽)×$\frac{4}{3}$= (长)
(长)×$\frac{2}{7}$= (高)
(2)六(1)班会游泳的学生占$\frac{3}{10}$,其中$\frac{1}{2}$是女生。
(六(1)班学生人数)×$\frac{3}{10}×\frac{1}{2}$= (会游泳的女生人数)

答案： 2.
(1)宽 长 长 高
(2)六
(1)班学生人数 会游泳的女生人数

3. 看图列式计算。

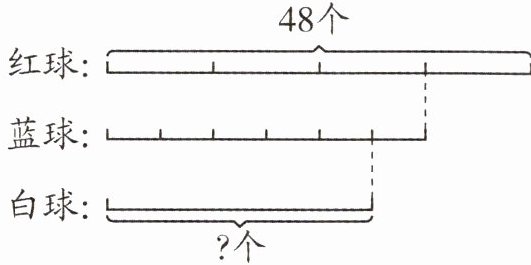
答案： 3. $48×\frac{3}{4}×\frac{5}{6}=30$(个)

4. 学校图书馆有2400本科技书,周五被借走了$\frac{5}{12}$,其中六年级借走了$\frac{3}{20}$。六年级借走了多少本科技书?

答案： 4. $2400×\frac{5}{12}×\frac{3}{20}=150$(本)
答:六年级借走了150本科技书。

5. 新趋势 结构补充 “古稀”“花甲”“不惑”等都是古代对年龄的称谓。其中“古稀”表示70岁,“花甲”表示的年龄是“古稀”的$\frac{6}{7}$,“不惑”表示的年龄是“花甲”的$\frac{2}{3}$。“不惑”表示的年龄是多少岁？在横线上补充合适的信息,使问题可以用算式“$70×\frac{6}{7}×\frac{2}{3}$”来解答,并解答出来。
$70×\frac{6}{7}×\frac{2}{3}=40$(岁)
答:“不惑”表示的年龄是40岁。

答案： 5. 补充的信息是“不惑”表示的年龄是“花甲”的$\frac{2}{3}$ $70×\frac{6}{7}×\frac{2}{3}=40$(岁)
答:“不惑”表示的年龄是40岁。

6. 计算:$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×…×\frac{99}{100}×\frac{100}{101}$

答案： 6. $\frac{1}{101}$ 提示:前一个分数的分母正好和后一个分数的分子约分,最后还剩第一个分数的分子和最后一个分数的分母,即$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}×\cdots×\frac{99}{100}×\frac{100}{101}=\frac{1}{101}$。

7. 一只皮球从25米的高处自由落下,接触地面后又立即弹起,再落下,又弹起,反复几次,每次弹起的高度是落下高度的$\frac{3}{5}$。第一次弹起的高度是多少米？第三次呢？

答案： 7. $25×\frac{3}{5}=15$(米) $15×\frac{3}{5}×\frac{3}{5}=\frac{27}{5}$(米)
答:第一次弹起的高度是15米,第三次弹起的高度是$\frac{27}{5}$米。 提示:从第二次开始,每次弹起的高度都是前一次弹起高度的$\frac{3}{5}$。