第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
| 测量长度 | 测量面积 | 测量体积 |
| 1 cm |$ 1 cm^2 $|$ 1 cm^3 $|
| (
归纳总结
它们度量的道理是(
| 1 cm |$ 1 cm^2 $|$ 1 cm^3 $|
| (
3
)cm |$ (6
)cm^2 $|$ (16
)cm^3 $|$ (5
)cm^3 $|归纳总结
它们度量的道理是(
相同
)(填“相同”或“不同”)的,都是度量单位的累加。
答案:
3 6 16 5 相同 提示:测量长度时,用一小段表示 1 厘米,有几个小段,就是几厘米,题图中是 3 个小段,就是 3 厘米;测量面积时,用一个小正方形表示 1 平方厘米,有几个小正方形,就是几平方厘米,题图中 6 个小正方形,就是 6 平方厘米;测量体积时,用一个小正方体表示 1 立方厘米,题图中左边有两层,每层是 8 个小正方体,一共是 8×2=16(个),就是 16 立方厘米;右边是两层,底层是 4 个,上层是 1 个,一共是 4+1=5(个)小正方体,就是 5 立方厘米。它们度量的道理是相同的,都是用一个单位的量进行度量。
2. 新情境 人文历史 商鞅方升是商鞅为秦国变法统一度量衡时所监制的标准量器,据史料记载,它的内长5.4寸,宽3寸,深1寸(寸为当时计量长度的单位)。它的容积为(
16.2
)立方寸(棱长为1寸的正方体,体积是1立方寸)。如果把8.1立方寸水倒进商鞅方升中,那么水深为(0.5
)寸。
答案:
16.2 0.5 提示:计算容器的容积,利用长方体体积计算公式:长方体的体积=长×宽×高,代入数据即可计算出它的容积,列式为 5.4×3×1=16.2(立方寸);用 8.1 立方寸除以容器的底面积,就可得 8.1 立方寸倒入容器里,容器内水的深度,列式为 8.1÷(5.4×3)=0.5(寸),即水深 0.5 寸。
3. 新情境 热点视窗 2024年,徐州博物馆举办圆明园兽首特展。下图是马首复制品的相关信息。
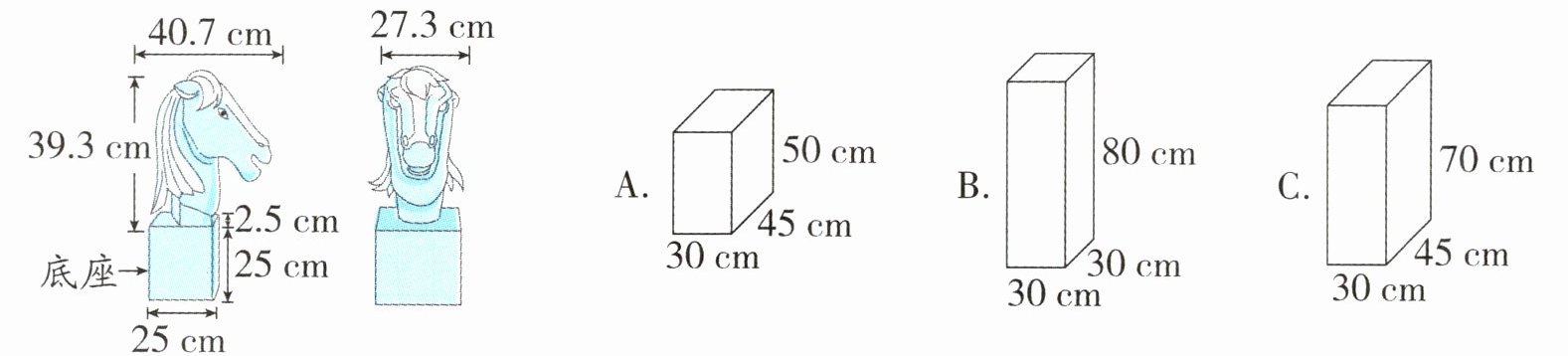
(1)如果要设计一个玻璃盒对马首(含底座)进行保护,选择右图(
(2)要制作选中的这个玻璃盒,至少需要多少平方分米的玻璃板?(接口处忽略不计,不含底面)

(1)如果要设计一个玻璃盒对马首(含底座)进行保护,选择右图(
C
)玻璃盒比较合适。(2)要制作选中的这个玻璃盒,至少需要多少平方分米的玻璃板?(接口处忽略不计,不含底面)
30×45+30×70×2+45×70×2=11850(平方厘米),11850平方厘米=118.5平方分米,答:至少需要118.5平方分米的玻璃板。
答案:
(1)C 提示:选择能容纳马首的玻璃盒,要保证玻璃盒的长、宽、高分别不小于马首的长、宽、高(含底座),马首的长是 40.7 厘米,宽是 27.3 厘米,高是 39.3+25=64.3(厘米),A 选项的高 50<64.3,不合适;B 选项,长 30<40.7,不合适;C 选项,45>40.7,30>27.3,70>64.3,长、宽、高分别大于马首的长、宽、高,合适,所以此题的正确选项是 C。
(2)30×45+30×70×2+45×70×2=11850(平方厘米) 11850 平方厘米=118.5 平方分米 答:至少需要 118.5 平方分米的玻璃板。提示:求制作这个玻璃盒需要的玻璃板的面积,就是求这个长方体玻璃盒的表面积,依据“长方体的表面积=(长×宽+长×高+宽×高)×2”代入数据计算即可,因为不含底面,所以只需求 5 个面的面积,长×宽的面是一个面,列式为 30×45+30×70×2+45×70×2=11850(平方厘米),再根据 1 平方分米=100 平方厘米,把单位进行转换,11850 平方厘米=118.5 平方分米,即至少需要 118.5 平方分米的玻璃板。
(1)C 提示:选择能容纳马首的玻璃盒,要保证玻璃盒的长、宽、高分别不小于马首的长、宽、高(含底座),马首的长是 40.7 厘米,宽是 27.3 厘米,高是 39.3+25=64.3(厘米),A 选项的高 50<64.3,不合适;B 选项,长 30<40.7,不合适;C 选项,45>40.7,30>27.3,70>64.3,长、宽、高分别大于马首的长、宽、高,合适,所以此题的正确选项是 C。
(2)30×45+30×70×2+45×70×2=11850(平方厘米) 11850 平方厘米=118.5 平方分米 答:至少需要 118.5 平方分米的玻璃板。提示:求制作这个玻璃盒需要的玻璃板的面积,就是求这个长方体玻璃盒的表面积,依据“长方体的表面积=(长×宽+长×高+宽×高)×2”代入数据计算即可,因为不含底面,所以只需求 5 个面的面积,长×宽的面是一个面,列式为 30×45+30×70×2+45×70×2=11850(平方厘米),再根据 1 平方分米=100 平方厘米,把单位进行转换,11850 平方厘米=118.5 平方分米,即至少需要 118.5 平方分米的玻璃板。
4. 新趋势 推导探究 图①、图②都是已学过的立体图形。图③是一个由底面是直角三角形、侧面是三个长方形围成的几何体,我们称为三棱柱。
(1)回顾已有知识:
$S_{长方体底面}= ab$
$V_{长方体}= abh$
$S_{正方体底面}= a^2$
$V_{正方体}= a^3$
 (2)发现共同规律:$V= 底面积×高$
(2)发现共同规律:$V= 底面积×高$
(3)推测新发现:$V_{三棱柱}= 底面积×高$
(4)尝试解决问题:根据你的发现,图③的体积是(
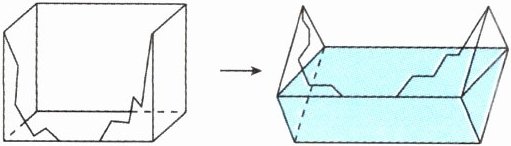
(5)生活实际运用:一个无盖的长方体玻璃缸,从里面量,长、宽、高分别为8分米、4分米、6分米。有一个面打碎了(非底面),现将鱼缸倾斜一定角度盛水。算一算这个坏的鱼缸最多能盛水多少升。
(1)回顾已有知识:
$S_{长方体底面}= ab$
$V_{长方体}= abh$
$S_{正方体底面}= a^2$
$V_{正方体}= a^3$
 (2)发现共同规律:$V= 底面积×高$
(2)发现共同规律:$V= 底面积×高$(3)推测新发现:$V_{三棱柱}= 底面积×高$
(4)尝试解决问题:根据你的发现,图③的体积是(
180
)立方厘米。(5)生活实际运用:一个无盖的长方体玻璃缸,从里面量,长、宽、高分别为8分米、4分米、6分米。有一个面打碎了(非底面),现将鱼缸倾斜一定角度盛水。算一算这个坏的鱼缸最多能盛水多少升。

96
答案:
(4)180 提示:
(1)~
(3)根据公式和发现的规律填空即可。
(4)6×6÷2×10=180(立方厘米)。
(5)4×6÷2×8=96(立方分米) 96 立方分米=96 升 答:这个坏的鱼缸最多能盛水 96 升。提示:
(5)这个坏的鱼缸最多能盛水的体积就是三棱柱的体积,三棱柱的高为 8 分米,底面直角三角形的面积为 4×6÷2=12(平方分米),所以体积为 12×8=96(立方分米),96 立方分米=96 升,这个坏的鱼缸最多能盛水 96 升。
(4)180 提示:
(1)~
(3)根据公式和发现的规律填空即可。
(4)6×6÷2×10=180(立方厘米)。
(5)4×6÷2×8=96(立方分米) 96 立方分米=96 升 答:这个坏的鱼缸最多能盛水 96 升。提示:
(5)这个坏的鱼缸最多能盛水的体积就是三棱柱的体积,三棱柱的高为 8 分米,底面直角三角形的面积为 4×6÷2=12(平方分米),所以体积为 12×8=96(立方分米),96 立方分米=96 升,这个坏的鱼缸最多能盛水 96 升。
查看更多完整答案,请扫码查看


