第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
(1)看图列式计算。
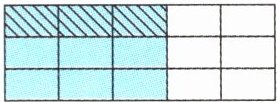
列式计算:$\frac{( )}{( )}×\frac{( )}{( )}= \frac{( )}{( )}$。

列式计算:$\frac{( )}{( )}×\frac{( )}{( )}= \frac{( )}{( )}$。
答案:
$\frac{3}{5}$×$\frac{1}{3}$=$\frac{1}{5}$
(2)$\frac{3}{4}米的\frac{3}{5}$是( )米,$\frac{14}{15}千克的\frac{5}{7}$是( )千克。
答案:
1. 首先计算$\frac{3}{4}$米的$\frac{3}{5}$:
根据求一个数的几分之几是多少用乘法计算,公式为$a×\frac{b}{c}=\frac{ab}{c}$($a = \frac{3}{4}$,$b = 3$,$c = 5$)。
则$\frac{3}{4}×\frac{3}{5}=\frac{3×3}{4×5}=\frac{9}{20}$(米)。
2. 然后计算$\frac{14}{15}$千克的$\frac{5}{7}$:
同样根据乘法公式$a×\frac{b}{c}=\frac{ab}{c}$($a=\frac{14}{15}$,$b = 5$,$c = 7$)。
$\frac{14}{15}×\frac{5}{7}=\frac{14×5}{15×7}$,约分可得$\frac{2}{3}$(千克)。
故答案依次为:$\frac{9}{20}$;$\frac{2}{3}$。
根据求一个数的几分之几是多少用乘法计算,公式为$a×\frac{b}{c}=\frac{ab}{c}$($a = \frac{3}{4}$,$b = 3$,$c = 5$)。
则$\frac{3}{4}×\frac{3}{5}=\frac{3×3}{4×5}=\frac{9}{20}$(米)。
2. 然后计算$\frac{14}{15}$千克的$\frac{5}{7}$:
同样根据乘法公式$a×\frac{b}{c}=\frac{ab}{c}$($a=\frac{14}{15}$,$b = 5$,$c = 7$)。
$\frac{14}{15}×\frac{5}{7}=\frac{14×5}{15×7}$,约分可得$\frac{2}{3}$(千克)。
故答案依次为:$\frac{9}{20}$;$\frac{2}{3}$。
2.直接写出得数。
$\frac{11}{18}×\frac{9}{22}= $( )
$\frac{3}{20}×5= $( )
$\frac{5}{21}×\frac{14}{15}= $( )
$\frac{2}{3}×\frac{6}{7}= $( )
$\frac{9}{10}×\frac{5}{6}= $( )
$\frac{9}{25}×\frac{5}{27}= $( )
$\frac{11}{18}×\frac{9}{22}= $( )
$\frac{3}{20}×5= $( )
$\frac{5}{21}×\frac{14}{15}= $( )
$\frac{2}{3}×\frac{6}{7}= $( )
$\frac{9}{10}×\frac{5}{6}= $( )
$\frac{9}{25}×\frac{5}{27}= $( )
答案:
$\frac{1}{4}$;$\frac{3}{4}$;$\frac{2}{9}$;$\frac{4}{7}$;$\frac{3}{4}$;$\frac{1}{15}$
(1)$\frac{3}{4}$米长的绳子,用去了$\frac{1}{6}$,剩下多少米?列式正确的是( )。
A.$\frac{3}{4}×\frac{1}{6}$
B.$\frac{3}{4}-\frac{1}{6}$
C.$\frac{3}{4}-\frac{3}{4}×\frac{1}{6}$
D.$\frac{3}{4}+\frac{1}{6}$
A.$\frac{3}{4}×\frac{1}{6}$
B.$\frac{3}{4}-\frac{1}{6}$
C.$\frac{3}{4}-\frac{3}{4}×\frac{1}{6}$
D.$\frac{3}{4}+\frac{1}{6}$
答案:
C
(2)下面( )的积在$\frac{1}{3}和\frac{5}{6}$之间。
A.$\frac{2}{3}×\frac{1}{3}$
B.$\frac{4}{7}×\frac{7}{8}$
C.$\frac{1}{5}×5$
D.$\frac{5}{9}×\frac{1}{5}$
A.$\frac{2}{3}×\frac{1}{3}$
B.$\frac{4}{7}×\frac{7}{8}$
C.$\frac{1}{5}×5$
D.$\frac{5}{9}×\frac{1}{5}$
答案:
B
4.(名校期末真题)陈东家有一块$\frac{1}{2}$公顷的土地,用它的$\frac{3}{5}$来种土豆。种土豆的面积是多少公顷?
(1)陈东用一个长方形表示1公顷,并画出了解决这个问题的示意图(如下图)。能表示解决这个问题的思考过程的图是(
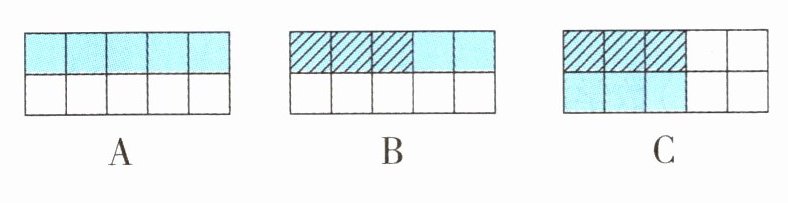
(2)列式计算:
(
(1)陈东用一个长方形表示1公顷,并画出了解决这个问题的示意图(如下图)。能表示解决这个问题的思考过程的图是(
B
)。
(2)列式计算:
(
$\frac{1}{2}$
)×($\frac{3}{5}$
)= ($\frac{3}{10}$
)(公顷)
答案:
(1)B
(2)$\frac{1}{2}$×$\frac{3}{5}$=$\frac{3}{10}$
(1)B
(2)$\frac{1}{2}$×$\frac{3}{5}$=$\frac{3}{10}$
5.一个长方形的长是$\frac{5}{8}$米,宽是长的$\frac{4}{5}$。这个长方形的宽是多少米?面积是多少平方米?
答案:
$\frac{5}{8}$×$\frac{4}{5}$=$\frac{1}{2}$(米) $\frac{5}{8}$×$\frac{1}{2}$=$\frac{5}{16}$(平方米)答:这个长方形的宽是$\frac{1}{2}$米,面积是$\frac{5}{16}$平方米。
6.如图,把一个三角形三条边上的中点连接起来,可以得到一个小三角形,再把小三角形三条边上的中点连接起来,又可以得到一个更小的三角形(图中涂色部分),如果大三角形的面积是$\frac{16}{5}$平方厘米,那么涂色三角形的面积是(
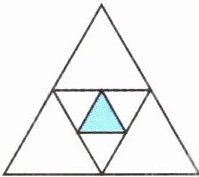
$\frac{1}{5}$
)平方厘米。
答案:
$\frac{1}{5}$ 提示:如图,把大三角形平均分成16份,所求部分占其中的1份,则所求部分的面积是大三角形面积的$\frac{1}{16}$,是$\frac{16}{5}$×$\frac{1}{16}$=$\frac{1}{5}$(平方厘米)。
7.(1)先计算,再观察每道算式的得数。
① $\frac{5}{2}+\frac{5}{3}= \frac{
② $\frac{9}{4}+\frac{9}{5}= \frac{
③ $\frac{10}{3}+\frac{10}{7}= \frac{
(2)根据(1)中的发现,写出下面算式的答案。
$\frac{20}{11}+\frac{20}{9}= \frac{
① $\frac{5}{2}+\frac{5}{3}= \frac{
25
}{6
}$ $\frac{5}{2}×\frac{5}{3}= \frac{25
}{6
}$② $\frac{9}{4}+\frac{9}{5}= \frac{
81
}{20
}$ $\frac{9}{4}×\frac{9}{5}= \frac{81
}{20
}$③ $\frac{10}{3}+\frac{10}{7}= \frac{
100
}{21
}$ $\frac{10}{3}×\frac{10}{7}= \frac{100
}{21
}$(2)根据(1)中的发现,写出下面算式的答案。
$\frac{20}{11}+\frac{20}{9}= \frac{
400
}{99
}$ $\frac{12}{7}+\frac{12}{5}= \frac{144
}{35
}$
答案:
(1)①$\frac{25}{6}$ $\frac{25}{6}$ ②$\frac{81}{20}$ $\frac{81}{20}$ ③$\frac{100}{21}$ $\frac{100}{21}$
(2)$\frac{400}{99}$ $\frac{144}{35}$ 提示:若两个分数的分子相同,且第一个分数的分母+第二个分数的分母=分子,那么这两个分数的和与积相等。所以$\frac{20}{11}$+$\frac{20}{9}$=$\frac{20×20}{11×9}$=$\frac{400}{99}$,$\frac{12}{7}$+$\frac{12}{5}$=$\frac{12×12}{7×5}$=$\frac{144}{35}$。
(1)①$\frac{25}{6}$ $\frac{25}{6}$ ②$\frac{81}{20}$ $\frac{81}{20}$ ③$\frac{100}{21}$ $\frac{100}{21}$
(2)$\frac{400}{99}$ $\frac{144}{35}$ 提示:若两个分数的分子相同,且第一个分数的分母+第二个分数的分母=分子,那么这两个分数的和与积相等。所以$\frac{20}{11}$+$\frac{20}{9}$=$\frac{20×20}{11×9}$=$\frac{400}{99}$,$\frac{12}{7}$+$\frac{12}{5}$=$\frac{12×12}{7×5}$=$\frac{144}{35}$。
查看更多完整答案,请扫码查看


