《2025年名校课堂七年级数学上册沪科版安徽专版》

1. 按一定规律排列的一列数依次是$\frac{2}{3},1,\frac{8}{7},\frac{11}{9},\frac{14}{11},\frac{17}{13},…$,则这列数的第 100 个数是 (B)
A.$\frac{299}{199}$
B.$\frac{299}{201}$
C.$\frac{301}{201}$
D.$\frac{303}{203}$

答案： B

2. (2024·合肥高新区期末)如图,这是一个按某种规律排列的数阵,根据规律,自然数 2 024 应该排在从上向下数的第$m$行,是该行中的从左向右数的第$n$个数,那么$m + n$的值是 (A)

A.133
B.131
C.130
D.128

答案： A

3. 将一列有理数：$-1,2,-3,4,-5,6,…$,按如图方式有序排列. 根据图中的排列规律可知,“峰 1”中峰顶的位置($C$的位置)是有理数 4,“峰 2”中峰顶的位置($C$的位置)是有理数$-9$.

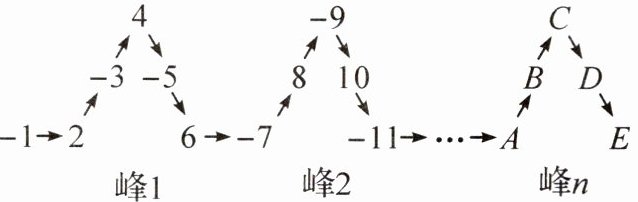
(1)“峰 3”中$C$的位置是有理数14；
(2)“峰$n$”中$C$的位置是有理数$(-1)^{n+1}(5n-1)$.

答案：
(1)14
(2)$(-1)^{n+1}(5n-1)$

4. (2023·山西)如图,这是一组有规律的图案,它由若干个大小相同的圆片组成. 第 1 个图案中有 4 个白色圆片,第 2 个图案中有 6 个白色圆片,第 3 个图案中有 8 个白色圆片,第 4 个图案中有 10 个白色圆片……依此规律,第$n$个图案中有$(2+2n)$个白色圆片(用含$n$的代数式表示).
]

答案： $(2+2n)$

5. (2023·合肥经开区期中改编)如图,这是由五角星摆成的三角形图案,每条边上有$n(n ＞ 1)$个五角星,每个图案的五角星总数用$S$表示.

(1)观察图案,当$n = 6$时,$S = $15；
(2)分析上面的一些特例,能得出怎样的规律？即$S = $$3n-3$；(用含$n的代数式表示S$)
(3)当$n = 2 025$时,求$S$的值.
当$n=2025$时,$S=3×2025-3=6072.$

答案： 解:
(1)15
(2)$3n-3$
(3)当$n=2025$时,$S=3×2025-3=6072.$

6. 观察等式：
①$2 = 1×2$；
②$2 + 4 = 6 = 2×3$；
③$2 + 4 + 6 = 12 = 3×4$；
……
按照这种规律写出第$n$个等式：$2 + 4 + 6 + … + 2n = $$n(n+1)$.

答案： $n(n+1)$

7. (2024·阜阳临泉县期末)观察下面的点阵图和相应的等式,探究其中的规律：

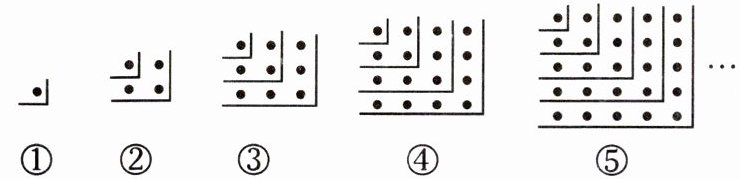
①$1 = 1^2$；②$1 + 3 = 2^2$；③$1 + 3 + 5 = 3^2$；④______.
(1)在④后面的横线上写出相应的等式；
(2)试用含$n$的式子表示这一规律：$1 + 3 + 5 + 7 + 9 + … +$______$= n^2$；($n$为正整数)
(3)请计算：$1 + 3 + 5 + 7 + … + 147 + 149$.
(1)$1+3+5+7=4^{2}$
(2)$(2n-1)$
(3)由(2)得,$1+3+5+7+... +147+149=75^{2}=5625.$

答案： 解:
(1)$1+3+5+7=4^{2}$
(2)$(2n-1)$
(3)由
(2)得,$1+3+5+7+... +147+149=75^{2}=5625.$