第105页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
10. 已知∠AOB= 70°,以O为端点作射线OC,使∠AOC= 42°,则∠BOC的度数为
28°或112°
.
答案:
28°或112°
11. (2023·北京)如图,∠AOC= ∠BOD= 90°,∠AOD= 126°,则∠BOC的度数为(
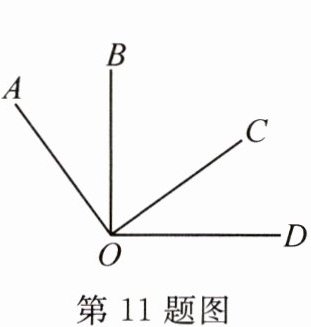
A.$36^{\circ}$
B.$44^{\circ}$
C.$54^{\circ}$
D.$63^{\circ}$
C
)
A.$36^{\circ}$
B.$44^{\circ}$
C.$54^{\circ}$
D.$63^{\circ}$
答案:
C
12. 下列所给的角:①$15^{\circ}$;②$65^{\circ}$;③$75^{\circ}$;④$115^{\circ}$;⑤$135^{\circ}$,其中可以用一副三角板画出来的是(
A.②④⑤
B.①②④
C.①③⑤
D.①③④
C
)A.②④⑤
B.①②④
C.①③⑤
D.①③④
答案:
C
13. (2024·淮北期末)如图,已知轮船A在灯塔P的北偏东30°25′方向上,轮船B在灯塔P东南方向,则∠APB的度数为

104°35′
.
答案:
104°35′
14. 如图,已知,OE平分∠AOB,OF平分∠BOC,∠EOF= 65°,则∠AOC=
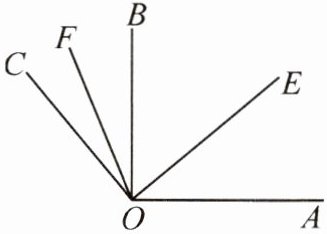
130
°.
答案:
130
15. (教材P164习题T8变式)(2024·合肥瑶海区期末)如图,已知∠COB= 2∠AOC,OD平分∠AOB.
(1)若∠COD= 20°,求∠AOB的度数;
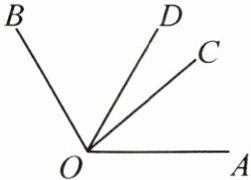
(2)若∠COD= $m^{\circ}$,求∠AOB的度数.
(1)若∠COD= 20°,求∠AOB的度数;

(2)若∠COD= $m^{\circ}$,求∠AOB的度数.
答案:
解:
(1)设∠AOC=x°.
∵∠COB=2∠AOC,
∴∠COB=2x°.
∴∠AOB=∠AOC+∠COB=3x°.
∵OD平分∠AOB,
∴∠AOD=∠BOD=1/2∠AOB=1.5x°.
∴∠COD=∠AOD-∠AOC=0.5x°=20°.
∴x=40.
∴∠AOB=3x°=3×40°=120°.
(2)同
(1)可得,∠COD=0.5x°=m°.
∴x=2m.
∴∠AOB=3x°=3×2m°=6m°.
(1)设∠AOC=x°.
∵∠COB=2∠AOC,
∴∠COB=2x°.
∴∠AOB=∠AOC+∠COB=3x°.
∵OD平分∠AOB,
∴∠AOD=∠BOD=1/2∠AOB=1.5x°.
∴∠COD=∠AOD-∠AOC=0.5x°=20°.
∴x=40.
∴∠AOB=3x°=3×40°=120°.
(2)同
(1)可得,∠COD=0.5x°=m°.
∴x=2m.
∴∠AOB=3x°=3×2m°=6m°.
16. (2023·合肥46中期末)探索新知:
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC.若其中有一个角的度数是另一个角度数的2倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线______这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN= α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ______;(用含α的代数式表示出所有可能的结果)
深入研究:
(3)如图2,若∠MPN= 60°,且射线PQ从PN位置出发,绕点P以每秒15°的速度逆时针旋转,当PQ与PN成180°时停止旋转,设旋转的时间为t秒.当t为何值时,射线PM是∠QPN的“巧分线”?
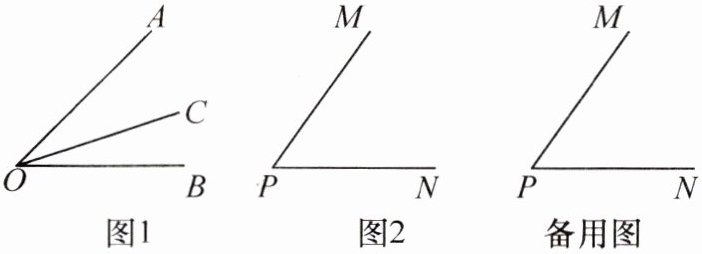
(1)
(2)
(3)
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC.若其中有一个角的度数是另一个角度数的2倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线______这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN= α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ______;(用含α的代数式表示出所有可能的结果)
深入研究:
(3)如图2,若∠MPN= 60°,且射线PQ从PN位置出发,绕点P以每秒15°的速度逆时针旋转,当PQ与PN成180°时停止旋转,设旋转的时间为t秒.当t为何值时,射线PM是∠QPN的“巧分线”?

(1)
是
(2)
$\frac{1}{3}\alpha$或$\frac{1}{2}\alpha$或$\frac{2}{3}\alpha$
(3)
$t = 6$或$t = 8$
答案:
1. (1)
因为角平分线将角分成两个相等的角,即一个角是另一个角的$2$倍($2$倍关系:$\angle AOB = 2\angle AOC=2\angle BOC$),所以一个角的平分线**是**这个角的“巧分线”。
2. (2)
已知$\angle MPN=\alpha$,射线$PQ$是$\angle MPN$的“巧分线”,分三种情况讨论:
当$\angle MPQ = 2\angle QPN$时,因为$\angle MPQ+\angle QPN=\angle MPN=\alpha$,即$2\angle QPN+\angle QPN=\alpha$,$3\angle QPN=\alpha$,$\angle QPN=\frac{1}{3}\alpha$,所以$\angle MPQ=\frac{2}{3}\alpha$;
当$\angle QPN = 2\angle MPQ$时,因为$\angle MPQ+\angle QPN=\angle MPN=\alpha$,即$\angle MPQ + 2\angle MPQ=\alpha$,$3\angle MPQ=\alpha$,所以$\angle MPQ=\frac{1}{3}\alpha$;
当$\angle MPN = 2\angle MPQ$时,$\angle MPQ=\frac{1}{2}\alpha$。
所以$\angle MPQ=\frac{1}{3}\alpha$或$\frac{1}{2}\alpha$或$\frac{2}{3}\alpha$。
3. (3)
解:已知$\angle MPN = 60^{\circ}$,$\angle QPN=15t^{\circ}$。
因为射线$PM$是$\angle QPN$的“巧分线”,分三种情况讨论:
①当$\angle QPM = 2\angle MPN$时,$\angle QPN=\angle QPM+\angle MPN$,$\angle QPM = 2×60^{\circ}=120^{\circ}$,$\angle QPN=\angle QPM+\angle MPN=180^{\circ}$(不符合$PQ$与$PN$成$180^{\circ}$时停止旋转的条件,舍去);
②当$\angle MPN = 2\angle QPM$时,$\angle QPM=\frac{1}{2}\angle MPN = 30^{\circ}$,则$\angle QPN=\angle QPM+\angle MPN=30^{\circ}+60^{\circ}=90^{\circ}$,又因为$\angle QPN = 15t^{\circ}$,所以$15t=90$,解得$t = 6$;
③当$\angle QPN = 2\angle MPN$时,$\angle QPN=2×60^{\circ}=120^{\circ}$,因为$\angle QPN = 15t^{\circ}$,所以$15t = 120$,解得$t = 8$。
综上,(1)是;(2)$\frac{1}{3}\alpha$或$\frac{1}{2}\alpha$或$\frac{2}{3}\alpha$;(3)$t = 6$或$t = 8$。
因为角平分线将角分成两个相等的角,即一个角是另一个角的$2$倍($2$倍关系:$\angle AOB = 2\angle AOC=2\angle BOC$),所以一个角的平分线**是**这个角的“巧分线”。
2. (2)
已知$\angle MPN=\alpha$,射线$PQ$是$\angle MPN$的“巧分线”,分三种情况讨论:
当$\angle MPQ = 2\angle QPN$时,因为$\angle MPQ+\angle QPN=\angle MPN=\alpha$,即$2\angle QPN+\angle QPN=\alpha$,$3\angle QPN=\alpha$,$\angle QPN=\frac{1}{3}\alpha$,所以$\angle MPQ=\frac{2}{3}\alpha$;
当$\angle QPN = 2\angle MPQ$时,因为$\angle MPQ+\angle QPN=\angle MPN=\alpha$,即$\angle MPQ + 2\angle MPQ=\alpha$,$3\angle MPQ=\alpha$,所以$\angle MPQ=\frac{1}{3}\alpha$;
当$\angle MPN = 2\angle MPQ$时,$\angle MPQ=\frac{1}{2}\alpha$。
所以$\angle MPQ=\frac{1}{3}\alpha$或$\frac{1}{2}\alpha$或$\frac{2}{3}\alpha$。
3. (3)
解:已知$\angle MPN = 60^{\circ}$,$\angle QPN=15t^{\circ}$。
因为射线$PM$是$\angle QPN$的“巧分线”,分三种情况讨论:
①当$\angle QPM = 2\angle MPN$时,$\angle QPN=\angle QPM+\angle MPN$,$\angle QPM = 2×60^{\circ}=120^{\circ}$,$\angle QPN=\angle QPM+\angle MPN=180^{\circ}$(不符合$PQ$与$PN$成$180^{\circ}$时停止旋转的条件,舍去);
②当$\angle MPN = 2\angle QPM$时,$\angle QPM=\frac{1}{2}\angle MPN = 30^{\circ}$,则$\angle QPN=\angle QPM+\angle MPN=30^{\circ}+60^{\circ}=90^{\circ}$,又因为$\angle QPN = 15t^{\circ}$,所以$15t=90$,解得$t = 6$;
③当$\angle QPN = 2\angle MPN$时,$\angle QPN=2×60^{\circ}=120^{\circ}$,因为$\angle QPN = 15t^{\circ}$,所以$15t = 120$,解得$t = 8$。
综上,(1)是;(2)$\frac{1}{3}\alpha$或$\frac{1}{2}\alpha$或$\frac{2}{3}\alpha$;(3)$t = 6$或$t = 8$。
查看更多完整答案,请扫码查看


