《2025年一遍过六年级数学上册苏教版》

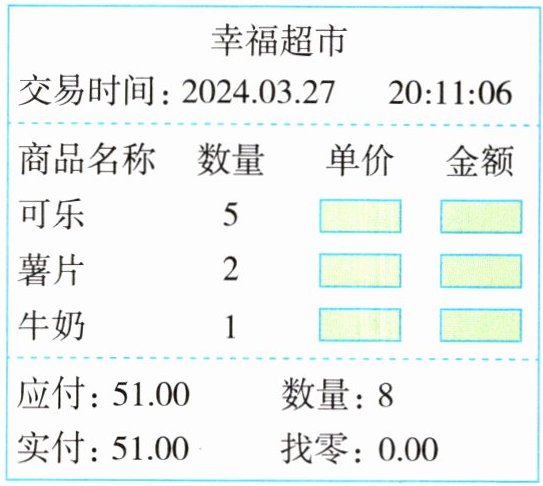
4 (情境题·生活情境)李明在超市买了零食,下面是他的购物小票。已知1桶牛奶的价钱相当于4袋薯片的总价钱,1袋薯片的价钱相当于2罐可乐的总价钱。这三种商品的单价各是多少?

答案： 4 可乐的单价:$51÷(5+2×2+1×4×2)=$3(元)
薯片的单价:$3×2=6$(元)
牛奶的单价:$6×4=24$(元)答:牛奶的单价是24元,薯片的单价是6元,可乐单价是3元。

5 小明期末考试语文、数学和英语的平均分是95分,数学比语文多6分,英语比语文多9分,小明三门功课各考了多少分?

答案： 解析：本题可根据平均数求出三门功课的总分，再结合数学、英语与语文的分数关系，通过设未知数列出方程求解。
1. 首先，根据“平均分是$95$分”求出三门功课的总分：
因为平均分$×$科目的数量$=$总分，所以三门功课的总分为$95×3 = 285$分。
2. 然后，设语文的成绩为$x$分，根据“数学比语文多$6$分”可知数学成绩为$(x + 6)$分，根据“英语比语文多$9$分”可知英语成绩为$(x + 9)$分。
3. 接着，根据三门功课的总分列出方程：
$x+(x + 6)+(x + 9)=285$
4. 再求解上述方程：
去括号得：$x+x + 6+x + 9=285$
合并同类项得：$3x+15 = 285$
方程两边同时减去$15$：$3x+15 - 15=285 - 15$，即$3x = 270$
方程两边同时除以$3$：$3x÷3 = 270÷3$，解得$x = 90$
5. 最后，求出数学和英语的成绩：
数学成绩：$x + 6=90 + 6 = 96$（分）
英语成绩：$x + 9=90 + 9 = 99$（分）
答案：语文$90$分，数学$96$分，英语$99$分。

6 (名校期末真题)李师傅、王师傅共同生产一种零件,李师傅生产了8小时,王师傅生产了6小时,他们一共生产了312个零件。已知王师傅5小时的工作量相当于李师傅2小时的工作量。李师傅和王师傅每小时各生产多少个零件?

答案： 解析：本题考查的是工作量，工作时间和工作效率的关系。
设李师傅每小时生产的零件数量为 $L$，王师傅每小时生产的零件数量为 $W$。
根据题目信息，李师傅生产了8小时，王师傅生产了6小时，他们一共生产了312个零件，可以得到方程：
$8L + 6W = 312$，
再根据题目中的信息，王师傅5小时的工作量相当于李师傅2小时的工作量，可以得到方程：
$5W = 2L$，
即$W = \frac{2}{5}L$，
将 $W = \frac{2}{5}L$ 代入$8L + 6W = 312$，得到：
$8L + 6 × \frac{2}{5}L = 312$，
化简得$8L + \frac{12}{5}L = 312$，
进一步化简得$\frac{40}{5}L + \frac{12}{5}L = 312$，
即$\frac{52}{5}L = 312$，
解得$L = 30$，
将 $L = 30$ 代入 $W = \frac{2}{5}L$ ，得到：
$W = \frac{2}{5} × 30$，
即$W = 12$，
所以，李师傅每小时生产30个零件，王师傅每小时生产12个零件。
答案：李师傅每小时生产30个零件，王师傅每小时生产12个零件。

7 为民粮店购进大米和面粉共236袋,当大米卖出一半时(面粉还未卖出),又购进28袋面粉,这时大米和面粉的袋数恰好相等。为民粮店原来购进面粉多少袋? (先将线段图补充完整,再解答)

答案： 解析：本题可通过设未知数，根据已知条件列出方程来求解原来购进面粉的袋数。
设为民粮店原来购进面粉$x$袋，因为大米和面粉共$236$袋，所以原来购进大米$(236 - x)$袋。
当大米卖出一半时，此时大米的袋数为$\frac{1}{2}(236 - x)$袋；又购进$28$袋面粉后，面粉的袋数为$(x + 28)$袋，且这时大米和面粉的袋数恰好相等，据此可列方程求解。
答案：解：设为民粮店原来购进面粉$x$袋，则原来购进大米$(236 - x)$袋。
$\frac{1}{2}(236 - x)=x + 28$
$118-\frac{1}{2}x=x + 28$
$x+\frac{1}{2}x=118 - 28$
$\frac{3}{2}x=90$
$x = 60$
答：为民粮店原来购进面粉$60$袋。

8 有一块长方形菜地,长20米。王奶奶要把这块地划分成两部分,分别用来种辣椒和白菜,并且要使种辣椒的面积是种白菜面积的7倍。用线段BE作为分割线(如图),请你计算出线段CE表示的实际长度。

答案： 设长方形菜地的宽为$ x $米，$ CE $的长度为$ y $米，则$ DE = 20 - y $米。
长方形面积：$ 20x $平方米。
白菜面积（三角形$ BCE $）：$ \frac{1}{2}xy $平方米。
辣椒面积 = 长方形面积 - 白菜面积 = $ 20x - \frac{1}{2}xy $平方米。
由辣椒面积是白菜面积的7倍，得：$ 20x - \frac{1}{2}xy = 7×\frac{1}{2}xy $
化简：$ 20x = 4xy $（$ x \neq 0 $，两边同除以$ x $）
$ 20 = 4y $
解得：$ y = 5 $
答：线段$ CE $的实际长度是5米。