第5页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
7. 质量均为 $ 1 \, kg $ 的铝块、铅块、水银和水($ c_{水} > c_{铝} > c_{水银} > c_{铅} $),将铝块和水银从 $ 40^{\circ}C $ 加热到 $ 50^{\circ}C $,铅块和水从 $ 10^{\circ}C $ 加热到 $ 20^{\circ}C $,则吸热最少的是(
A.铝块
B.水
C.铅块
D.水银
C
)A.铝块
B.水
C.铅块
D.水银
答案:
C
8. 由铜制成的甲、乙两物体,已知它们的质量之比为 $ 1 : 2 $,甲的温度升高了 $ 5^{\circ}C $,乙的温度升高了 $ 4^{\circ}C $,那么它们的比热容之比为
1:1
,吸收的热量之比为5:8
。
答案:
1:1 5:8
9. “卡路里”简称“卡”,是热量的另一个单位,现在仍被广泛使用在营养计量中。“卡”的规定是:$ 1 $ 卡等于在一标准大气压下,$ 1 \, g $ 水温度升高 $ 1^{\circ}C $ 吸收的热量。那么 $ 1 $ 卡等于
4.2
$ J $。若一个成年人参加一次长跑,身体消耗的能量约 $ 8.4 × 10^6 \, J $,相当于消耗$ 2× 10^{6} $
卡。$ [c_{水} = 4.2 × 10^3 \, J/(kg·^{\circ}C)] $
答案:
4.2 $ 2× 10^{6} $
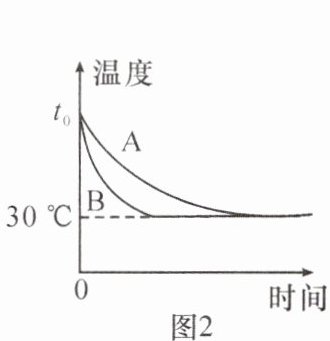
10. (2024·镇江)为比较 $ A $、$ B $ 两保温杯的保温性能,小红在两个保温杯中分别倒入 $ 0.1 \, kg $ 相同温度的热水,用温度计测量其初温 $ t_0 $,示数如图 1 所示,$ t_0 = $

80
$ ^{\circ}C $。绘制水温随时间的变化图像如图 2 所示,$ A $ 杯中水放出的热量为$ 2.1× 10^{4} $
$ J $,保温性能更好的是A
(填“$ A $”或“$ B $”)杯。$ [c_{水} = 4.2 × 10^3 \, J/(kg·^{\circ}C)] $

答案:
80 $ 2.1× 10^{4} $ A
11. 在标准大气压下,妈妈用热水给小明加热盒装牛奶,使牛奶的温度由 $ 20^{\circ}C $ 升高到 $ 62^{\circ}C $,牛奶的质量为 $ 250 \, g $,求:$ [已知 c_{水} = 4.2 × 10^3 \, J/(kg·^{\circ}C), c_{牛奶} = 2.5 × 10^3 \, J/(kg·^{\circ}C)] $
(1)牛奶吸收的热量。
(2)若不考虑热量损失,热水放出的热量全部被牛奶吸收,加热牛奶需要 $ 87^{\circ}C $ 的热水的质量。
(3)若水壶中 $ 87^{\circ}C $ 的水还有 $ 500 \, g $,它们再吸收 $ 4.2 × 10^4 \, J $ 的热量,壶中剩余水升高的温度。
(1)牛奶吸收的热量。
(2)若不考虑热量损失,热水放出的热量全部被牛奶吸收,加热牛奶需要 $ 87^{\circ}C $ 的热水的质量。
(3)若水壶中 $ 87^{\circ}C $ 的水还有 $ 500 \, g $,它们再吸收 $ 4.2 × 10^4 \, J $ 的热量,壶中剩余水升高的温度。
答案:
解:
(1)牛奶吸收的热量:$ Q_{吸}=c_{牛奶}m_{牛奶}(t-t_{0})=2.5× 10^{3}\ J/(kg\cdot^{\circ}C)× 250× 10^{-3}\ kg×(62\ ^{\circ}C-20\ ^{\circ}C)=2.625× 10^{4}\ J $
(2)不计热损失,热水放出的热量:$ Q_{放}=Q_{吸}=2.625× 10^{4}\ J $热水的质量:$ m_{水}=\frac{Q_{放}}{c_{水}(t_{水}-t)}=\frac{2.625× 10^{4}\ J}{4.2× 10^{3}\ J/(kg\cdot^{\circ}C)×(87\ ^{\circ}C-62\ ^{\circ}C)}=0.25\ kg $
(3)壶中剩余的水升高的温度:$ \Delta t=\frac{Q_{吸}'}{c_{水}m'}=\frac{4.2× 10^{4}\ J}{4.2× 10^{3}\ J/(kg\cdot^{\circ}C)× 0.5\ kg}=20\ ^{\circ}C $$ 87\ ^{\circ}C+20\ ^{\circ}C=107\ ^{\circ}C>100\ ^{\circ}C $在标准大气压下,水的沸点为 $ 100\ ^{\circ}C $,故水的实际末温为$ 100\ ^{\circ}C $,壶中剩余的水实际升高的温度:$ 100\ ^{\circ}C-87\ ^{\circ}C=13\ ^{\circ}C $
(1)牛奶吸收的热量:$ Q_{吸}=c_{牛奶}m_{牛奶}(t-t_{0})=2.5× 10^{3}\ J/(kg\cdot^{\circ}C)× 250× 10^{-3}\ kg×(62\ ^{\circ}C-20\ ^{\circ}C)=2.625× 10^{4}\ J $
(2)不计热损失,热水放出的热量:$ Q_{放}=Q_{吸}=2.625× 10^{4}\ J $热水的质量:$ m_{水}=\frac{Q_{放}}{c_{水}(t_{水}-t)}=\frac{2.625× 10^{4}\ J}{4.2× 10^{3}\ J/(kg\cdot^{\circ}C)×(87\ ^{\circ}C-62\ ^{\circ}C)}=0.25\ kg $
(3)壶中剩余的水升高的温度:$ \Delta t=\frac{Q_{吸}'}{c_{水}m'}=\frac{4.2× 10^{4}\ J}{4.2× 10^{3}\ J/(kg\cdot^{\circ}C)× 0.5\ kg}=20\ ^{\circ}C $$ 87\ ^{\circ}C+20\ ^{\circ}C=107\ ^{\circ}C>100\ ^{\circ}C $在标准大气压下,水的沸点为 $ 100\ ^{\circ}C $,故水的实际末温为$ 100\ ^{\circ}C $,壶中剩余的水实际升高的温度:$ 100\ ^{\circ}C-87\ ^{\circ}C=13\ ^{\circ}C $
12. (双选)质量均为 $ 0.5 \, kg $ 的水和另一种液体,在相同时间内放出的热量相等,它们的温度随时间变化的关系如图。已知水的比热容 $ c_{水} = 4.2 × 10^3 \, J/(kg·^{\circ}C) $,$ c_{水} > c_{液} $。下列说法中正确的是(
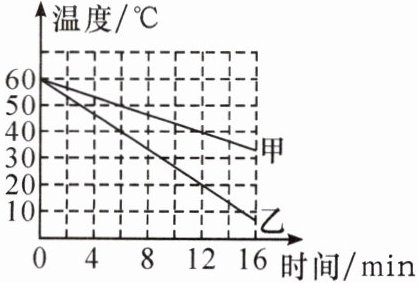
A.甲物质是水
B.$ 0 \sim 12 \, min $,乙的温度降低了 $ 20^{\circ}C $
C.$ 0 \sim 12 \, min $,甲放出了 $ 8.4 × 10^4 \, J $ 的热量
D.乙物质的比热容为 $ 2.1 × 10^3 \, J/(kg·^{\circ}C) $
AD
)
A.甲物质是水
B.$ 0 \sim 12 \, min $,乙的温度降低了 $ 20^{\circ}C $
C.$ 0 \sim 12 \, min $,甲放出了 $ 8.4 × 10^4 \, J $ 的热量
D.乙物质的比热容为 $ 2.1 × 10^3 \, J/(kg·^{\circ}C) $
答案:
AD
查看更多完整答案,请扫码查看


