《2025年暑假乐园辽宁师范大学出版社八年级理科版》

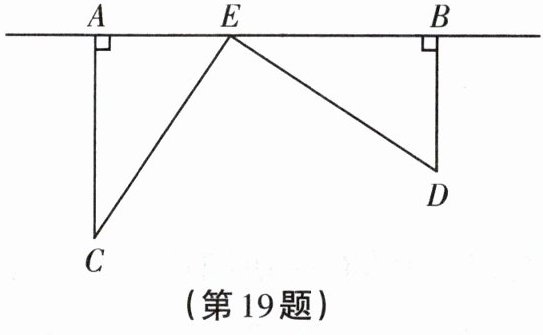
19. 为了丰富少年儿童的业余生活, 某社区要在如图所示的 $AB$ 所在直线上建一图书馆 $E$.本社区的两所学校所在的位置分别在点 $C$ 和点 $D$ 处, 且 $CA \perp AB$ 于点 $A,DB \perp AB$ 于点 $B$,已知 $AB = 25\mathrm{km},CA = 15\mathrm{km},DB = 10\mathrm{km}$, 试问: 图书馆 $E$ 应建在距点 $A$ 多少千米处, 才能使它到两所学校的距离相等?

答：图书馆 E 应建在距点 A 10 km 处.

答案： 图书馆 E 应建在距点 A 10 km 处

20. 在如图所示的 $\mathrm{Rt}\triangle ABC$ 中, $\angle B = 90^{\circ}$, 点 $P$ 从点 $B$ 出发沿 $BA$ 边以 $1\mathrm{cm/s}$ 的速度向点 $A$移动; 同时, 点 $Q$ 也从点 $B$ 出发沿 $BC$ 边以 $2\mathrm{cm/s}$ 的速度向点 $C$ 移动. 若 $AB,BC$足够长, 则$\sqrt{35}$秒后 $\triangle PBQ$ 的面积为 $35\mathrm{cm}^{2}$? 此时,$P,Q$ 两点间的距离是$5\sqrt{7}$厘米?(结果用最简二次根式表示)

答案： 本题可先根据三角形面积公式列出方程求出运动时间，再根据勾股定理求出$P$、$Q$两点间的距离。
步骤一：求运动时间
设$x$秒后$\triangle PBQ$的面积为$35\mathrm{cm}^{2}$。
已知点$P$的速度是$1\mathrm{cm/s}$，则$BP = x\mathrm{cm}$；点$Q$的速度是$2\mathrm{cm/s}$，则$BQ = 2x\mathrm{cm}$。
因为$\angle B = 90^{\circ}$，根据直角三角形面积公式$S=\frac{1}{2}ah$（其中$a$为底，$h$为高），可得$\triangle PBQ$的面积为$\frac{1}{2}BP\cdot BQ$，则可列出方程：
$\frac{1}{2}× x× 2x = 35$
化简方程$\frac{1}{2}× x× 2x = 35$可得$x^{2}=35$。
求解方程$x^{2}=35$，因为$x\gt0$，所以$x = \sqrt{35}$。
步骤二：求$P$、$Q$两点间的距离
在$\mathrm{Rt}\triangle PBQ$中，$\angle B = 90^{\circ}$，根据勾股定理$a^2+b^2=c^2$（其中$a$、$b$为直角边，$c$为斜边），可得$PQ=\sqrt{BP^{2} + BQ^{2}}$。
将$BP = \sqrt{35}\mathrm{cm}$，$BQ = 2\sqrt{35}\mathrm{cm}$代入上式可得：
$PQ=\sqrt{(\sqrt{35})^{2} + (2\sqrt{35})^{2}}=\sqrt{35 + 140}=\sqrt{175}=5\sqrt{7}(\mathrm{cm})$
综上，$\boldsymbol{\sqrt{35}}$秒后$\triangle PBQ$的面积为$35\mathrm{cm}^{2}$，此时$P$、$Q$两点间的距离是$\boldsymbol{5\sqrt{7}}$厘米。