2025年暑假乐园辽宁师范大学出版社八年级理科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假乐园辽宁师范大学出版社八年级理科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
14. 如图,方格中小正方形的边长为$1$,$\triangle A B C$的三个顶点都在格点(网格线的交点)上。
(1)请判断$\triangle A B C$是否为直角三角形,并说明理由。
$\triangle ABC$是直角三角形,理由:$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,$AC = 5$,满足$AB^{2}+BC^{2}=AC^{2}$
(2)求$\triangle A B C$的面积。
(1)请判断$\triangle A B C$是否为直角三角形,并说明理由。
$\triangle ABC$是直角三角形,理由:$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,$AC = 5$,满足$AB^{2}+BC^{2}=AC^{2}$
(2)求$\triangle A B C$的面积。
5
答案:
1. (1)
首先,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a$、$b$为直角边,$c$为斜边)计算$AB$、$BC$、$AC$的长度:
由勾股定理可得$AB=\sqrt{1^{2}+2^{2}}=\sqrt{1 + 4}=\sqrt{5}$;
$BC=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$;
$AC=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
然后,验证勾股定理的逆定理:
计算$AB^{2}+BC^{2}$的值:$AB^{2}+BC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=5 + 20=25$。
又因为$AC^{2}=25$,所以$AB^{2}+BC^{2}=AC^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$、$b$、$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\triangle ABC$是直角三角形。
2. (2)
解:根据三角形面积公式$S=\frac{1}{2}ab$($a$、$b$为直角边),
已知$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,
则$S_{\triangle ABC}=\frac{1}{2}× AB× BC$。
把$AB=\sqrt{5}$,$BC = 2\sqrt{5}$代入可得:$S_{\triangle ABC}=\frac{1}{2}×\sqrt{5}×2\sqrt{5}$。
根据二次根式乘法法则$\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}(a\geq0,b\geq0)$,则$\frac{1}{2}×\sqrt{5}×2\sqrt{5}=\frac{1}{2}×2×\sqrt{5×5}$。
计算得$S_{\triangle ABC}=5$。
综上,(1)$\triangle ABC$是直角三角形,理由:$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,$AC = 5$,满足$AB^{2}+BC^{2}=AC^{2}$;(2)$\triangle ABC$的面积为$5$。
首先,根据勾股定理$a^{2}+b^{2}=c^{2}$(其中$a$、$b$为直角边,$c$为斜边)计算$AB$、$BC$、$AC$的长度:
由勾股定理可得$AB=\sqrt{1^{2}+2^{2}}=\sqrt{1 + 4}=\sqrt{5}$;
$BC=\sqrt{2^{2}+4^{2}}=\sqrt{4 + 16}=\sqrt{20}=2\sqrt{5}$;
$AC=\sqrt{3^{2}+4^{2}}=\sqrt{9 + 16}=\sqrt{25}=5$。
然后,验证勾股定理的逆定理:
计算$AB^{2}+BC^{2}$的值:$AB^{2}+BC^{2}=(\sqrt{5})^{2}+(2\sqrt{5})^{2}=5 + 20=25$。
又因为$AC^{2}=25$,所以$AB^{2}+BC^{2}=AC^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$、$b$、$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\triangle ABC$是直角三角形。
2. (2)
解:根据三角形面积公式$S=\frac{1}{2}ab$($a$、$b$为直角边),
已知$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,
则$S_{\triangle ABC}=\frac{1}{2}× AB× BC$。
把$AB=\sqrt{5}$,$BC = 2\sqrt{5}$代入可得:$S_{\triangle ABC}=\frac{1}{2}×\sqrt{5}×2\sqrt{5}$。
根据二次根式乘法法则$\sqrt{a}\cdot\sqrt{b}=\sqrt{ab}(a\geq0,b\geq0)$,则$\frac{1}{2}×\sqrt{5}×2\sqrt{5}=\frac{1}{2}×2×\sqrt{5×5}$。
计算得$S_{\triangle ABC}=5$。
综上,(1)$\triangle ABC$是直角三角形,理由:$AB=\sqrt{5}$,$BC = 2\sqrt{5}$,$AC = 5$,满足$AB^{2}+BC^{2}=AC^{2}$;(2)$\triangle ABC$的面积为$5$。
15. 如图,在$\triangle A B C$中,$A B = B C$,$B E \perp A C$于点$E$,$A D \perp B C$于点$D$,$\angle B A D = 45 ^ { \circ }$,$A D$与$B E$交于点$F$,连接$C F$。
(1)求证:$B F = 2 A E$。
(2)若$C D = \sqrt { 2 }$,求$A D$的长。
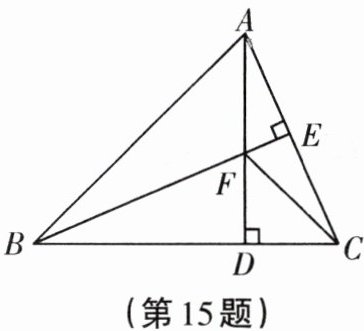
(1)证明:∵AD⊥BC,∠BAD=45°,∴∠ABD=∠BAD=45°.∴AD=BD.∵AD⊥BC,BE⊥AC,∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,∴∠CAD=∠CBE.又∵∠CDA=∠FDB=90°,∴△ADC≌△BDF;∴AC=BF.∵AB=BC,BE⊥AC,∴AE=EC,即AC=2AE,∴BF=2AE.
(2)解:∵△ADC≌△BDF,∴FD=CD=$\sqrt{2}$.∴在Rt△CDF中,CF=$\sqrt{FD²+CD²}$=2.∵BE⊥AC,AE=EC,∴AF=FC=2,∴AD=AF+FD=
(1)求证:$B F = 2 A E$。
(2)若$C D = \sqrt { 2 }$,求$A D$的长。

(1)证明:∵AD⊥BC,∠BAD=45°,∴∠ABD=∠BAD=45°.∴AD=BD.∵AD⊥BC,BE⊥AC,∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,∴∠CAD=∠CBE.又∵∠CDA=∠FDB=90°,∴△ADC≌△BDF;∴AC=BF.∵AB=BC,BE⊥AC,∴AE=EC,即AC=2AE,∴BF=2AE.
(2)解:∵△ADC≌△BDF,∴FD=CD=$\sqrt{2}$.∴在Rt△CDF中,CF=$\sqrt{FD²+CD²}$=2.∵BE⊥AC,AE=EC,∴AF=FC=2,∴AD=AF+FD=
2+$\sqrt{2}$
.
答案:
(1)证明:
∵AD⊥BC,∠BAD=45°,
∴∠ABD=∠BAD=45°.
∴AD=BD.
∵AD⊥
BC,BE⊥AC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE.又
∵∠CDA=∠FDB=90°,
∴△ADC≌△BDF;
∴AC=BF.
∵AB=BC,BE⊥AC,
∴AE=EC,即AC=2AE,
∴BF=2AE.
(2)解:
∵△ADC≌△BDF,
∴FD=CD=$\sqrt{2}$
∴在Rt△CDF中,CF=$\sqrt{FD²+CD²}$=2.
∵BE⊥AC,AE=EC,
∴AF=FC=2,
∴AD=
AF+FD=2+$\sqrt{2}$
(1)证明:
∵AD⊥BC,∠BAD=45°,
∴∠ABD=∠BAD=45°.
∴AD=BD.
∵AD⊥
BC,BE⊥AC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE.又
∵∠CDA=∠FDB=90°,
∴△ADC≌△BDF;
∴AC=BF.
∵AB=BC,BE⊥AC,
∴AE=EC,即AC=2AE,
∴BF=2AE.
(2)解:
∵△ADC≌△BDF,
∴FD=CD=$\sqrt{2}$
∴在Rt△CDF中,CF=$\sqrt{FD²+CD²}$=2.
∵BE⊥AC,AE=EC,
∴AF=FC=2,
∴AD=
AF+FD=2+$\sqrt{2}$
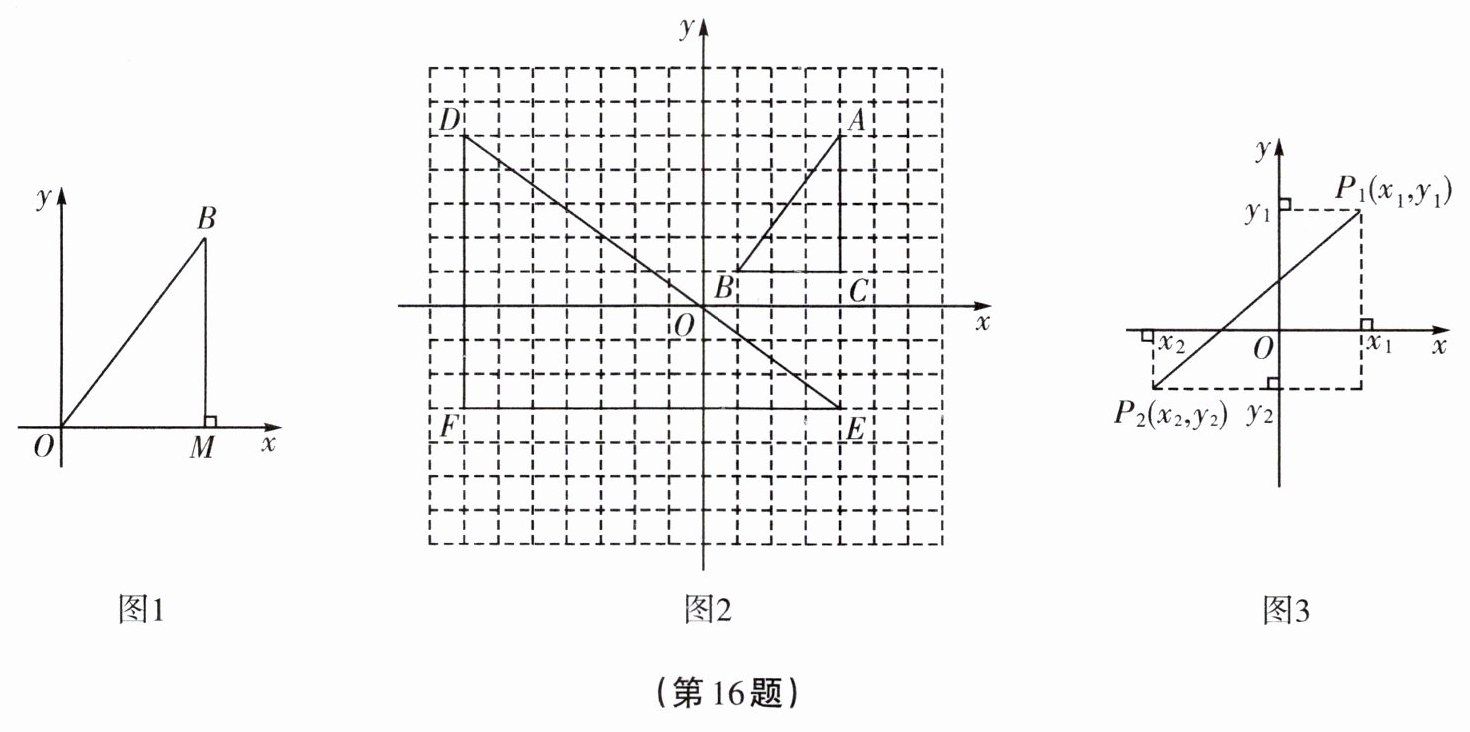
16. 【问题提出】
问题一:平面直角坐标系中,如果$A$,$B$是$x$轴上的两点,它们对应的横坐标分别是$x _ { A }$,$x _ { B }$,$C$,$D$是$y$轴上的两点,它们对应的纵坐标分别是$y _ { C }$,$y _ { D }$,那么$A$,$B$两点间的距离,$C$,$D$两点间的距离分别是多少?
问题二:平面直角坐标系中任意一点$P ( x , y )$到原点的距离是多少?
问题三:已知平面内的两点$P _ { 1 } ( x _ { 1 } , y _ { 1 } )$,$P _ { 2 } ( x _ { 2 } , y _ { 2 } )$,如何求点$P _ { 1 }$,$P _ { 2 }$间的距离$| P _ { 1 } P _ { 2 } |$?
【问题探究】
(1)求平面直角坐标系中同一坐标轴上两点之间的距离,可以借助绝对值来解决:$x$轴上的两点$E ( 5 , 0 )$,$F ( - 2 , 0 )$之间的距离$| E F | = | 5 - ( - 2 ) | = 7$,$y$轴上的两点$M ( 0 , 3 )$,$N ( 0 , 5 )$之间的距离$| M N | = | 3 - 5 | = 2$。
结论:在平面直角坐标系中,如果$A$,$B$是$x$轴上两点,它们的横坐标分别是$x _ { A }$,$x _ { B }$,那么$A$,$B$两点间的距离$| A B | =$______;如果$C$,$D$是$y$轴上的两点,它们的纵坐标分别是$y _ { C }$,$y _ { D }$,那么$C$,$D$两点间的距离$| C D | =$______。
(2)如图1,在平面直角坐标系中,点$B$的坐标为$( 3 , 4 )$,过点$B$向$x$轴作垂线,垂足为点$M$,由勾股定理得$| O B | =$______。
结论:平面直角坐标系中任意一点$P ( x , y )$到原点的距离$| O P | =$______。
(3)如图2,要求线段$D E$的长,可以转化为求$\mathrm { Rt } \triangle D E F$的斜边长,从坐标系中可以得出$D ( - 7 , 5 )$,$E ( 4 , - 3 )$,所以$| D F | = | 5 - ( - 3 ) | = 8$,$| E F | = | 4 - ( - 7 ) | = 11$,所以由勾股定理得$| D E | = \sqrt { 8 ^ { 2 } + 11 ^ { 2 } } = \sqrt { 185 }$。
请用上面的方法求图2中线段$A B$的长:$| A B | =$______。
在图3中,设$P _ { 1 } ( x _ { 1 } , y _ { 1 } )$,$P _ { 2 } ( x _ { 2 } , y _ { 2 } )$,试用含$x _ { 1 }$,$x _ { 2 }$,$y _ { 1 }$,$y _ { 2 }$的式子表示$P _ { 1 } P _ { 2 }$的长:$| P _ { 1 } P _ { 2 } | =$______。
【拓展应用】
试用以上结论解答下列问题:
已知平面直角坐标系中点$G ( 0 , 1 )$,$H ( 4 , 3 )$。
(4)若直线$G H$与$x$轴交于点$K$,求线段$H K$的长。
(5)若$T$为坐标轴上的点,且使得$\triangle G H T$是以$G H$为底边的等腰三角形,则点$T$的坐标为______(直接写出结果)。
问题一:平面直角坐标系中,如果$A$,$B$是$x$轴上的两点,它们对应的横坐标分别是$x _ { A }$,$x _ { B }$,$C$,$D$是$y$轴上的两点,它们对应的纵坐标分别是$y _ { C }$,$y _ { D }$,那么$A$,$B$两点间的距离,$C$,$D$两点间的距离分别是多少?
问题二:平面直角坐标系中任意一点$P ( x , y )$到原点的距离是多少?
问题三:已知平面内的两点$P _ { 1 } ( x _ { 1 } , y _ { 1 } )$,$P _ { 2 } ( x _ { 2 } , y _ { 2 } )$,如何求点$P _ { 1 }$,$P _ { 2 }$间的距离$| P _ { 1 } P _ { 2 } |$?
【问题探究】
(1)求平面直角坐标系中同一坐标轴上两点之间的距离,可以借助绝对值来解决:$x$轴上的两点$E ( 5 , 0 )$,$F ( - 2 , 0 )$之间的距离$| E F | = | 5 - ( - 2 ) | = 7$,$y$轴上的两点$M ( 0 , 3 )$,$N ( 0 , 5 )$之间的距离$| M N | = | 3 - 5 | = 2$。
结论:在平面直角坐标系中,如果$A$,$B$是$x$轴上两点,它们的横坐标分别是$x _ { A }$,$x _ { B }$,那么$A$,$B$两点间的距离$| A B | =$______;如果$C$,$D$是$y$轴上的两点,它们的纵坐标分别是$y _ { C }$,$y _ { D }$,那么$C$,$D$两点间的距离$| C D | =$______。
(2)如图1,在平面直角坐标系中,点$B$的坐标为$( 3 , 4 )$,过点$B$向$x$轴作垂线,垂足为点$M$,由勾股定理得$| O B | =$______。
结论:平面直角坐标系中任意一点$P ( x , y )$到原点的距离$| O P | =$______。
(3)如图2,要求线段$D E$的长,可以转化为求$\mathrm { Rt } \triangle D E F$的斜边长,从坐标系中可以得出$D ( - 7 , 5 )$,$E ( 4 , - 3 )$,所以$| D F | = | 5 - ( - 3 ) | = 8$,$| E F | = | 4 - ( - 7 ) | = 11$,所以由勾股定理得$| D E | = \sqrt { 8 ^ { 2 } + 11 ^ { 2 } } = \sqrt { 185 }$。
请用上面的方法求图2中线段$A B$的长:$| A B | =$______。
在图3中,设$P _ { 1 } ( x _ { 1 } , y _ { 1 } )$,$P _ { 2 } ( x _ { 2 } , y _ { 2 } )$,试用含$x _ { 1 }$,$x _ { 2 }$,$y _ { 1 }$,$y _ { 2 }$的式子表示$P _ { 1 } P _ { 2 }$的长:$| P _ { 1 } P _ { 2 } | =$______。
【拓展应用】
试用以上结论解答下列问题:
已知平面直角坐标系中点$G ( 0 , 1 )$,$H ( 4 , 3 )$。
(4)若直线$G H$与$x$轴交于点$K$,求线段$H K$的长。
(5)若$T$为坐标轴上的点,且使得$\triangle G H T$是以$G H$为底边的等腰三角形,则点$T$的坐标为______(直接写出结果)。

答案:
(1)|xA - xB| |yC - yD|
(2)5 $\sqrt{x²+y²}$
(3)5 $\sqrt{(x_1 - x_2)²+(y_1 - y_2)²}$
(4)如图,由图象可知K(−2,0).
∵H(4,3),
∴|HK|=$\sqrt{6²+3²}$=3$\sqrt{5}$
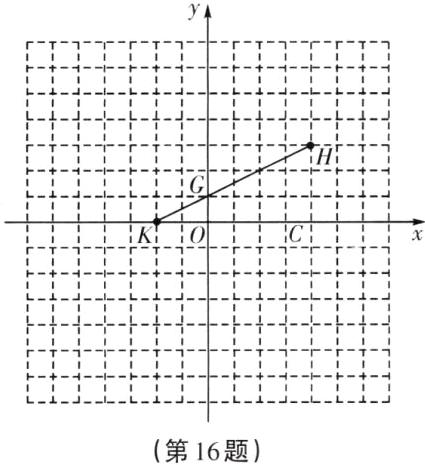
(5)(3,0)或(0,6)
(1)|xA - xB| |yC - yD|
(2)5 $\sqrt{x²+y²}$
(3)5 $\sqrt{(x_1 - x_2)²+(y_1 - y_2)²}$
(4)如图,由图象可知K(−2,0).
∵H(4,3),
∴|HK|=$\sqrt{6²+3²}$=3$\sqrt{5}$

(5)(3,0)或(0,6)
查看更多完整答案,请扫码查看


